Центрипетално убрзање - излазна формула и практична примјена

Центрипетално убрзање нас прати свуда. То чини наше Земља ротира око Сунца. Резултат гравитације нам омогућава да постојимо на овој планети. Како се може схватити шта је центрипетално убрзање? Дефиниција ове физичке количине представљена је у наставку.

Опажања

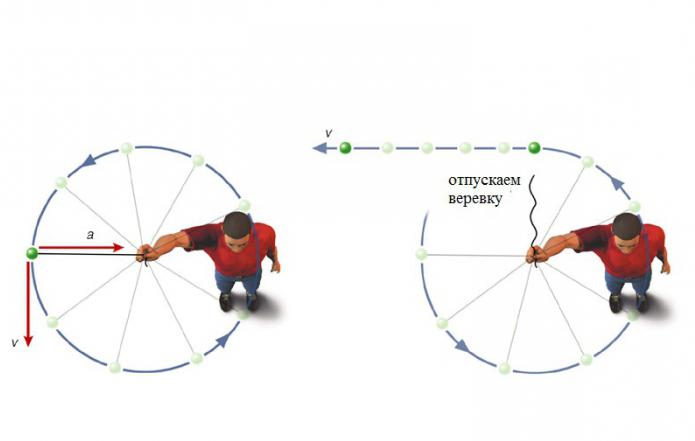
Најједноставнији примјер убрзања тијела које се креће у кругу може се видјети ротирањем камена на ужету. Повучеш конопац и конопац повлачи камен до центра. У сваком тренутку, конопац говори камену одређену количину покрета, и сваки пут - у новом правцу. Можете замислити кретање ужета у облику низа слабих трзаја. Трзај - и коноп мијења смјер, други кретен - још једна промјена, и тако даље у круг. Ако изненада ослободите конопац, кретени ће се зауставити, и заједно са њима ће се зауставити промјена смјера брзине. Камен ће се померити у правцу тангенте на круг. Поставља се питање: "Са којим убрзањем ће се тело померити у овом тренутку?"

Центрипетална формула убрзања

Прије свега, вриједи напоменути да је кретање тијела у кругу тешко. Камен истовремено учествује у два типа кретања: под дејством силе, креће се ка центру ротације, а истовремено тангенцијално на круг, удаљава се од овог центра. Према Њутновом другом закону, сила која држи камен на ужету је усмерена ка центру ротације дуж овог ужета. Такође ће бити усмерени на вектор убрзања.

Нека неко време, наш камен, крећући се равномерно брзином В, дође од тачке А до тачке Б. Претпоставимо да је у тренутку када је тело прешло тачку Б центрипетална сила престала да делује на њу. Тада би у одређеном временском периоду пао на тачку К. Лежи на тангенти. Ако би у истом тренутку само центрипеталне силе деловале на тело, онда би се за време т, крећући се истим убрзањем, појавило у тачки О, која се налази на правој линији, која представља пречник круга. Оба сегмента су вектори и поштују правило вектора. Као резултат сумирања ових двају кретања у временском интервалу т добијамо резултујуће кретање дуж лука АБ.

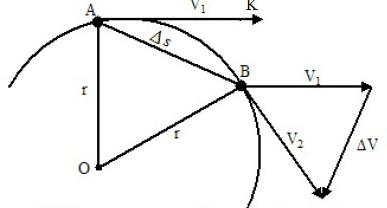
Ако се временски интервал т сматра занемарљивим, онда се лук АБ мало разликује од акорда АБ. Према томе, могуће је замијенити кретање дуж лука уз помицање уздуж тетиве. У овом случају, кретање камена дуж тетиве ће поштовати законе праволинијског кретања, тј. Пређена удаљеност АБ ће бити једнака производу брзине камена у време његовог кретања. АБ = В к т.

Означити жељено центрипетално убрзање словом а. Тада се пут који се покрива само дејством центрипеталног убрзања може израчунати користећи формулу једнолико убрзаног кретања:

АО = на 2/2.

Размак АБ је једнак продукту брзине и времена, тј. АБ = В к т,

АО - претходно израчуната по формули равномерно убрзано кретање за кретање у правој линији: АО = на 2/2.

Замењујући ове податке у формулу и трансформишући их, добијамо једноставну и елегантну центрипеталну формулу убрзања:

а = в ² / Р

Ово се може изразити ријечима на сљедећи начин: центрипетално убрзање тијела које се креће у кругу једнако је квоцијенту од дијељења линеарне брзине квадриране полупречником круга у којем се тијело ротира. Центрипетална сила у овом случају ће изгледати као слика испод.

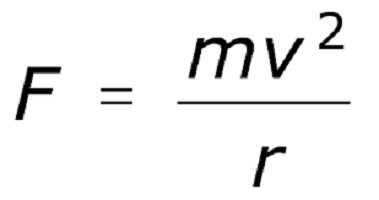
Угаона брзина

Угаона брзина једнак количнику линеарне брзине подељен са радијусом круга. Обрнуто је исто: В = ωР, где је ω угаона брзина

Ако замените ову вредност у формули, можете добити израз центрифугалног убрзања за угаону брзину. Изгледаће овако:

а = ω ² Р.

Убрзање без промене брзине

Па ипак, зашто се тело са убрзањем усмереним ка центру не креће брже и не приближава се центру ротације? Одговор лежи у самој формулацији убрзања. Чињенице указују да је вожња у кругу стварна, али да би се одржала, потребно је убрзање усмјерено према центру. Под дејством силе изазване овим убрзањем долази до промене количине кретања, због чега се путања кретања стално савија, мењајући правац вектора брзине све време, али не мењајући његову апсолутну вредност. Крећући се у кругу, наш дуготрајни камен улази унутра, иначе ће наставити да се креће по тангенти. Сваки тренутак времена, остављајући га на тангенти, камен привлачи центар, али не пада у њега. Други пример центрипеталног убрзања може бити водени скијаш, описујући мале кругове на води. Фигура спортисте је нагнута; чини се да пада, настављајући да се креће и нагиње се напред.

Тако можемо закључити да убрзање не повећава брзину тела, јер су вектори брзине и убрзања окомити један на други. Додавањем вектора брзине, убрзање само мења правац кретања и држи тело у орбити.

Вишак границе сигурности

У претходном искуству бавили смо се идеалним конопцем који није био подеран. Али, рецимо, наш конопац је најчешћи и чак можете израчунати силу, након чега ће се једноставно сломити. Да би се израчунала ова сила, довољно је упоредити сигурносну маргину ужета са оптерећењем које доживљава у процесу ротације камена. Окретањем камена бржом брзином, дајете јој више покрета, што значи више убрзања.

Са пречником уже од јуте од око 20 мм, његова влачна чврстоћа је око 26 кН. Важно је напоменути да се дужина ужета не појављује нигдје. Ротирајући оптерећење од 1 кг величине на ужету са радијусом од 1 м, може се израчунати да је линеарна брзина потребна за ломљење 26 к 10 ³ = 1 кг к В 2/1 м. 26 к 10 ³ = 161 м / с.

Гравитација

Када смо размотрили искуство, занемарили смо акцију гравитација пошто је на тако високим брзинама његов утицај занемарљив. Али можете видјети да када одмотавање дугачког ужета, тијело описује сложенију путању и поступно се приближава тлу.

Небеска тела

Ако пренесемо законе кретања дуж круга у простор и применимо их на кретање небеска тела Можете поново отворити неколико познатих формула. На пример, сила којом тело привлачи Земљу је позната по формули:

Ф = м * г.

У нашем случају, фактор г је управо центрипетално убрзање, које је изведено из претходне формуле. Само у овом случају улогу камена ће извршити небеско тело, привучено Земљом, а улога ће бити у сили гравитације. Мултипликатор г ће бити изражен кроз радијус наше планете и брзину његове ротације.

Резултати

Суштина центрипеталног убрзања састоји се у тешком и незахвалном послу одржавања покретног тела у орбити. Постоји парадоксалан случај када, уз константно убрзање, тијело не мијења величину своје брзине. За нетрениран ум, таква изјава је прилично парадоксална. Ипак, у прорачуну кретања електрона око језгра, и при израчунавању брзине ротације звезде око црне рупе, центрипетално убрзање не игра последњу улогу.