Како израчунати углове између вектора?

Када проучавамо геометрију, појављује се много питања на тему вектора. Ученик има посебне тешкоће када је у питању проналажење углова између вектора.

Основни појмови

Пре разматрања углова између вектора, потребно је упознати дефиницију вектора и концепт угла између вектора.

Вектор је сегмент који има правац, односно сегмент за који је дефинисан његов почетак и крај.

Угао између два вектора на равни која има заједнички почетак назива се мањи од углова, чијом количином желите да померите један од вектора око заједничке тачке, до позиције у којој се њихови правци поклапају.

Формула за решавање

Разумејући шта је вектор и како се одређује његов угао, можемо израчунати угао између вектора. Формула за ово решење је прилично једноставна, а резултат њене примене биће вредност косинуса угла. Према дефиницији, она је једнака одређеном скаларном производу вектора и производу њихових дужина.

Скаларни производ вектора се сматра сумом одговарајућих координата вектора фактора помножених једна са другом. Дужина вектора, или његов модул, се рачуна као скуаре роот од сума квадрата његових координата.

Пошто је добијена вредност косинуса угла, величина самог угла се може израчунати помоћу калкулатора или помоћу тригонометријске табеле.

Пример

Када схватите како да израчунате угао између вектора, решење одговарајућег проблема ће постати једноставно и јасно. Као пример, вреди размотрити једноставан задатак проналажења величине угла.

Прије свега, бит ће прикладније израчунати потребну вриједност за рјешавање вриједности дужина вектора и њиховог скаларног производа. Користећи горе описани опис добијамо:

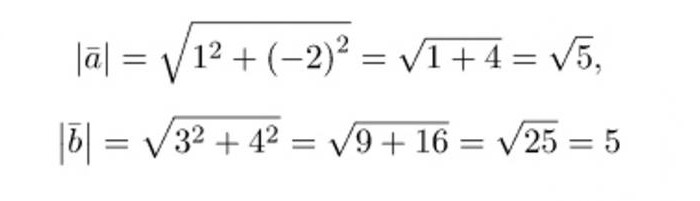
Замењујући добијене вредности у формулу, израчунавамо косинус жељеног угла:

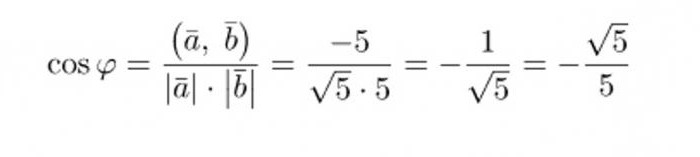
Овај број није једна од пет уобичајених вредности косинуса, тако да за добијање угла морате користити калкулатор или тригонометријску табелу Брадиса. Али пре него што добијемо угао између вектора, формула се може поједноставити да се ослободи додатног негативног знака:

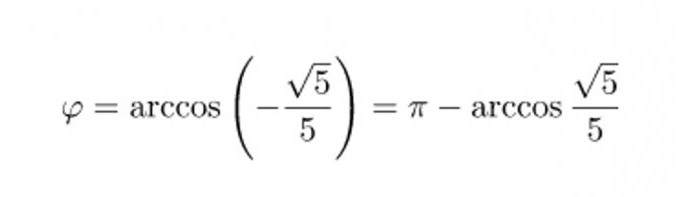
Коначни одговор за одржавање тачности може бити остављен у овом облику, а угао можете израчунати у степенима. Према табели Брадиса, његова вредност ће бити око 116 степени и 70 минута, а калкулатор ће показати вредност од 116,57 степени.

Израчунајте угао у н-димензионалном простору

Када разматрамо два вектора у тродимензионални простор много је теже схватити који је кутак у питању ако не леже у истој равни. Да бисте поједноставили перцепцију, можете нацртати два сечена сегмента, који формирају најмањи угао између њих, и то ће бити жељени. Упркос присуству треће координате у вектору, процес израчунавања углова између вектора се неће променити. Израчунајте скаларни производ и модуле вектора, лук косинус њиховог приватног и одговор на овај проблем.

У геометрији, често постоје проблеми са просторима који имају више од три димензије. Али за њих, алгоритам за проналажење одговора изгледа исто.

Разлика између 0 и 180 степени

Једна од најчешћих грешака приликом писања одговора на проблем дизајниран за израчунавање угла између вектора је одлука да се запише да су вектори паралелни, односно, жељени угао је 0 или 180 степени. Овај одговор је нетачан.

Добивши вредност угла од 0 степени према резултатима одлуке, тачан одговор би био да се вектори одреде као усмерени, тј. Вектори ће имати исти правац. У случају 180 степени, вектори ће бити супротно усмерени.

Специфиц Вецторс

Проналажењем углова између вектора, можете пронаћи један од специјалних типова, поред оних који су описани у претходном тексту.

• Неколико вектора паралелно једној равни називају се копланарни.
• Вектори исте дужине и правца се називају једнаки.
• Вектори који леже на једној правој линији, без обзира на правац, називају се колинеарни.
• Ако је дужина вектора нула, односно њен почетак и крај се подударају, онда се она зове нула, а ако је једна, онда је то јединица.