Како спровести студију пуне функције

У овом чланку размотрићемо шему за проучавање функције и дати примере студија о екстремима, монотонији и асимптотама ове функције.

Сцхеме

1. Функција области постојања (ДХС).
2. Пресјек функције (ако постоји) са осима координата, знакова функције, паритета, периодичности.
3. Преломне тачке (њихов род). Континуитет. Вертикалне асимптоте.
4. Монотонија и екстремне тачке.
5. Тачке инфлексије Булге
6. Проучавање функције на бесконачности, на асимптотама: хоризонтално и косо.
7. Плоттинг.

Монотони студи

Теорем. Ако је функција г континуирана на [а, б] , диференцирана са (а; б) и г '(к) ≥ 0 (г' (к) ≤0) , ке (а; б) , тада се г повећава (смањује) за [а, б] .

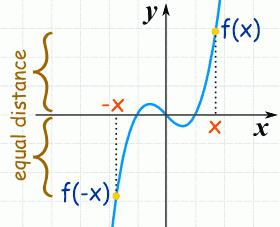
Пример:

и = 1: 3к ³ - 6: 2к ² + 5к.

ДХС: кР

и '= к ² + 6к + 5.

Пронађи интервале константних знакова и ' . Пошто је и ' елементарна функција, може да мења знакове само на тачкама где се окреће на нулу или не постоји. Њен ДХС: кР .

Пронађите тачке чији је дериват 0 (нула):

и '= 0;

к = -1; -5.

Дакле, и расте на (-∞; -5] и на [-1; + ∞), и силазно до [1; 2] .

Ектреме Студи

Т. к _{0 се} назива максимална тачка (мак) на скупу А функције г када се вредност г (к ₀ ) ≥ г (к), кеА узима као функција у овој тачки.

Т. к _{0 се} назива минимална тачка (мин) функције г на скупу А када се најмањи г (к ₀ ) ≤ г (к), кеА узима као функција у овој тачки .

На скупу А максималне тачке (мак) и минимум (мин) називају се екстремним тачкама г. Такве екстреме се називају и апсолутним екстремима на сету .

Ако је к ₀ екстремна тачка г у неком округу, онда се к ₀ означава као локална или локална екстремна тачка (мак или мин) од г.

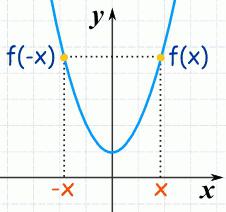
Теорем (захтевано стање). Ако је к ₀ екстремна тачка (локалне) функције г , онда дериват не постоји или је једнак у овој р. 0 (нули).

Дефиниција Критичне тачке су тачке са непостојећим или једнаким 0 (нултим) дериватом. Ове тачке података су сумњиве за екстрем.

Теорема (услов бр. 1). Ако је функција г континуирана у одређеном сусједству т. Кс ₀ и знак мијења свој дериват на пријелазу, тада је задана точка екстрема г.

Теорема (услов бр. 2). Нека се функција у одређеном дистрикту диференцира два пута и г '= 0, и г' '> 0 (г' '<0) , онда ова тачка је тачка максималне (мак) или минималне (мин) функције.

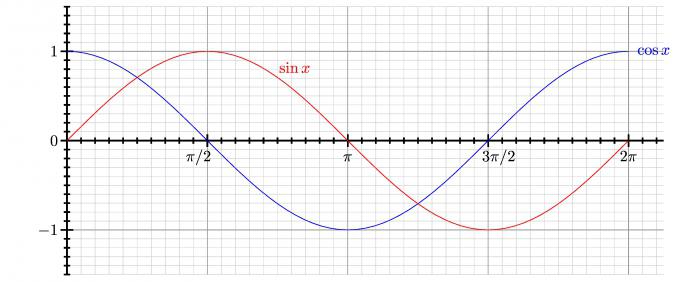
Студија булге

Функција се назива конвексна (или конкавна) на интервалу (а, б) када граф функције није виши од секанта на интервалу за било који к са (а, б) који пролази кроз ове тачке .

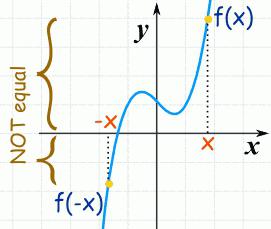
Функција ће бити конвексна строго доле на (а, б) , ако - графикон лежи испод секанта на размаку.

Функција се назива конвексна (конвексна) на интервалу (а, б) , ако је за било које т тачке с (а, б) граф функције функције на интервалу није нижи од секанта који пролази кроз апсцисе у овим тачкама .

Функција ће бити строго конвексна према горе на (а, б ), ако - граф на интервалу лежи изнад секанта.

Ако је функција у дистрикту точка је континуирана и након т. к ₀ функција мијења конвексност на пријелазу, а та се точка назива точка инфлексије функције.

Асимптоте тест

Дефиниција Правац се назива асимптот г (к) ако се на бесконачној удаљености од извора координата приближи точка графа функције: д (М, л).

Асимптоти могу бити вертикални, хоризонтални и коси.

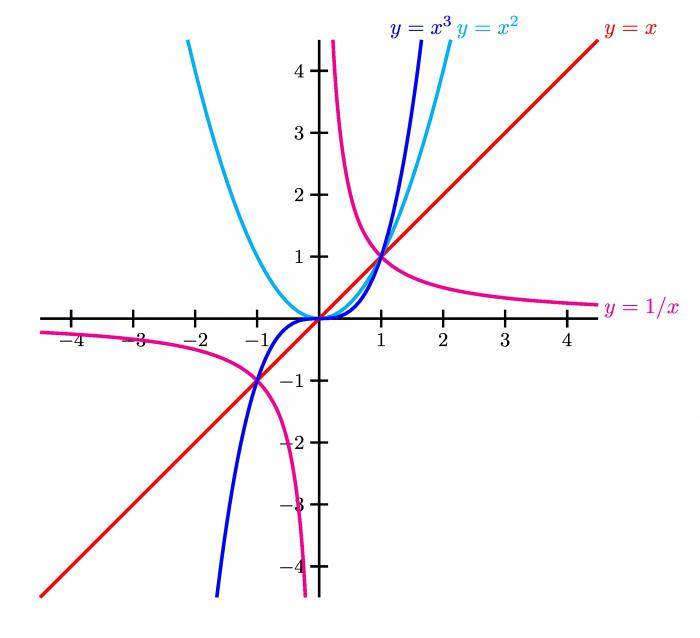
Вертикална линија са једнаџбом к = к ₀ ће бити асимптота вертикалног графа функције г иф ин т. к _{0 је} бесконачна празнина, тј. најмање једна лева или десна граница у овом тренутку је бесконачност.

Проучавање функције на сегменту на вредности најмањих и највећих

Ако је функција континуирана на [а, б] , онда према Веиерстрассовој теореми постоји највећа вредност и најмања вредност на том сегменту, тј. Постоје т тачке које припадају [а, б] тако да је г (к ₁ ) ≤ г (к) <г (к ₂ ), к _{2 е} [а, б]. Из теорема о монотоности и екстремима добијамо следећу шему за проучавање функције на сегменту за најмању и највећу вредност.

План

1. Пронађите дериват г '(к) .
2. На овим местима и на крајевима сегмента пронађите вредност функције г.
3. Пронађене вредности упоређују и селектују најмањи и највећи.

Ремарк Ако желите да проучите функцију на коначном интервалу (а, б) или на бесконачном (-∞; б); (-∞; + ∞) на мак и мин вредности, затим у плану, уместо вредности функције на крајевима празнине, претражују се одговарајуће једностране границе: умјесто ф (а), тражи се ф (а +) = лимф (к) , уместо ф (б), ф (-б) Тако да можете наћи ЛДУ функције на интервалу, јер апсолутни екстреми не морају нужно постојати у овом случају.

Примена деривата на решавање примењених проблема на екстрему одређених величина

1. Изразите ову вредност у смислу других вредности из стања проблема тако да је функција само једне променљиве (ако је могуће).
2. Одредите период промене ове променљиве.
3. Провести проучавање функције на интервалу при мак и мин вриједностима.

Задатак. Неопходно је изградити правоугаону платформу, користећи решеткасте метре, уз зид тако да се на једној страни уклапа у зид, а на друге три је ограђена решетком. У којем омјеру ће највећа бити површина таквог мјеста?

С = ки је функција 2 варијабле.

С = к (а - 2к) - функција 1. варијабле ; к е [0; а: 2].

С = ак - 2к ² ; С '= а - 4к = 0, кеР, к = а: 4.

С (а: 4) = а ² : 8 је највећа вредност;

С (0) = 0.

Пронађите другу страну правоугаоника: = а: 2.

Омјер слике: и: к = 2.

Одговор је. Највећа површина ће бити једнака 2/8 , ако је страна која је паралелна са зидом 2 пута већа од друге стране.

Функција истраживања. Примери

Пример 1

Постоји и = к ³ : (1-к) ² . Извођење истраживања.

1. ДХС: ке (-∞; 1) У (1; ∞).
2. Општи облик функције (ниједан ни непаран) није симетричан око тачке 0 (нула).
3. Знакови функције. Функција је елементарна, тако да може променити само знак у тачкама где је 0 (нула), или не постоји.
4. Функција је елементарна, дакле континуирана на ДХС-у: (-); 1) У (1; ∞).

Гап: к = 1;

лимк ³ : (1 - к) ² = ∞ - Дисконтинуитет друге врсте (бесконачан), тако да у тачки 1 постоји вертикална асимптота;

к = 1 је вертикална асимптотска једначина.

5. и '= к ² (3 - к): (1 - к) ³ ;

ДХС (и '): к; 1;

к = 1 - критична тачка.

и '= 0;

0; 3 - критичне тачке.

6. и "= 6к: (1 - к) ⁴ ;

Критична т: 1, 0;

к = 0 - м. кинк, и (0) = 0.

7. лимк ³ : (1 - 2к + к ² ) = ∞ - нема хоризонталне асимптоте, али може бити нагнуто.

к = 1 је број;

б = 2 је број.

Дакле, постоји асимптота која је нагнута и = к + 2 на + ∞ и на - ∞.

Пример 2

Дато и = (к ² + 1): (к - 1). Да правим и истражујем. Изградите граф.

1. Домена постојања је читава нумеричка линија, осим м. Кс = 1 .

2. и сече ОИ (ако је могуће) у м. (0; г (0)) . Нађи и (0) = -1 - т .

Тачке пресека графа налазимо са ОКС решавањем једначине и = 0 . Роот екуатион нема валидан, стога ова функција не сијече ОКС .

3. Функција није периодична. Размотрите израз

г (-к) (г (к), и г (-к) -г (к) . То значи да је ово генеричка функција (ни чак ни непарна).

4. Т. к = 1 јаз има другу врсту. У свим другим тачкама функција је континуирана.

5 Проучавање функције на екстрему:

(к ² - 2к - 1): (к - 1) ² = и '

и решити једначину и '= 0.

Дакле, 1 - ,2, 1 + √2, 1 - критичне тачке или тачке могућег екстрема. Ове тачке деле нумеричку линију на четири интервала .

У сваком интервалу, дериват има одређени знак, који се може поставити методом интервала или израчунавањем вриједности деривата на појединачним тачкама. На интервалима (-∞; 1 - )2) У ( 1 + ;2; ∞) , позитивни дериват значи да функција расте; ако је ке ( 1 - ;2; 1) У (1; 1 + √2 ) , функција се смањује, јер је у тим интервалима дериват негативан. Кроз т. Кс ₁ када се креће (померањем с лева на десно) мења изведени знак из "+" у "-", дакле, у овом тренутку постоји локални максимум, налазимо

и _мак = 2 - 2 .2 .

Када пролазите кроз к _{2, он} мења изведени знак из "-" у "+", тако да у овом тренутку постоји локални минимум, и

и _мик = 2 + 2√2.

Т. к = 1 није тако екстреман.

6. 4: (к - 1) ³ = и ".

У (-∞; 1 ) 0> и " , сходно томе, на овом интервалу крива је конвексна; ако је ке ( 1 ; ∞) - крива је конкавна. У тачки 1, функција није дефинисана, тако да ова тачка није тачка инфлексије.

7 Из резултата параграфа 4 следи да је к = 1 вертикална крива асимптоте.

Хоризонталне асимптоте су одсутне.

к + 1 = и је асимптота склоној овој кривој. Нема других асимптота.

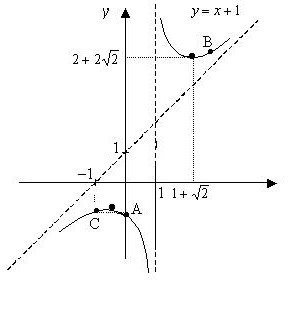
8. Узимајући у обзир спроведено истраживање, градимо графикон (види слику горе).