Како пронаћи подручје полигона?

Код проблема на геометрији често је потребно израчунати површину полигона. Штавише, он може имати прилично различит облик - од познатог троугла до одређеног н-кута са неким незамисливим бројем врхова. Поред тога, ови полигони су конвексни или конкавни. У свакој ситуацији треба да се гради на изгледу фигуре. Тако да се испоставља да изаберете најбољи начин за решавање проблема. Облик може бити исправан, што ће значајно поједноставити рјешење проблема.

Мало теорије полигона

Ако су нацртане три или више правих линија које се укрштају, онда оне формирају одређену фигуру. То је полигон. По броју тачака пресека, постаје јасно колико ће то тачака имати. Они дају име настале фигуре. То може бити:

• троугао;
• четверокут;
• пента или шестерокут и тако даље.

Такву цифру ће сигурно карактерисати две одредбе:

1. Суседне стране не припадају једној правој линији.
2. Не-суседне тачке немају заједничке тачке, тј. Не секу се.

Да бисте разумели које су тачке суседне, морате да видите да ли припадају истој страни. Ако јесте, следећи. У супротном, могу бити повезани сегментом, који се назива дијагонала. Они се могу нацртати само у полигонима који имају више од три врха.

Које су њихове врсте?

Полигон са више од четири угла може бити конвексан или конкаван. Разлика је у томе што неки од њених врхова могу лежати на супротним странама равне линије која се извлачи кроз произвољну страну полигона. У конвексном, сви врхови увек леже на једној страни такве линије.

У школском току геометрије, највећи део времена је дат тачно конвексним фигурама. Дакле, у проблемима је потребно открити подручје конвексног полигона. Затим постоји формула преко радијуса описне кружнице, која вам омогућава да пронађете жељену вредност за било који облик. У другим случајевима, јединствено рјешење не постоји. За троугао, формула је једна, а за квадрат или трапез потпуно другачија. У ситуацијама када је број погрешан или има много врхова, уобичајено је да се поделе на једноставне и познате.

Шта учинити ако комад има три или четири вертицес?

У првом случају то ће бити троугао и можете користити једну од формула:

• С = 1/2 * а * н, где је а страна, н је висина до ње;
• С = 1/2 * а * б * син (А), где су а и б стране троугла, А је угао између познатих страна;
• С = √ (п * (п - а) * (п - ц) * (п - ц)), где је ц страна троугла, до већ обележених два, п је полу - периметар, односно сума све три стране, подељене у две .

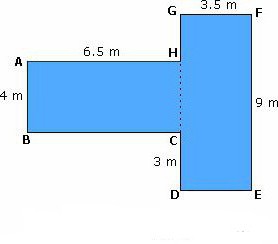
Слика са четири врха може бити паралелограм:

• С = а * н;
• С = 1/2 * д ₁ * д ₂ * син (α), где су д ₁ и д ₂ дијагонале, α је угао између њих;
• С = а * ин * син (α).

Формула фор трапезна подручја: С = н * (а + б) / 2, где су а и б дужине база.

Шта урадити са регуларним полигоном са више од четири врха?

За почетак, такву цифру карактерише чињеница да су у њој све стране једнаке. Плус, полигон има исте углове.

Ако се око такве фигуре описује круг, онда се његов радијус поклапа са сегментом од центра полигона до једног од врхова. Дакле, да бисмо израчунали површину регуларног полигона са произвољним бројем врхова, потребна нам је следећа формула:

С _н = 1/2 * н * Р _н ² * син (360º / н), где је н број врхова полигона.

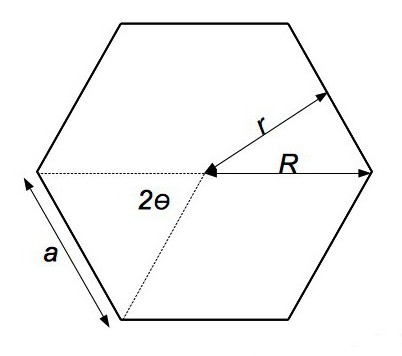
Из њега је лако добити онај који је користан за посебне случајеве:

1. троуглови: С = (3√3) / 4 * Р2;
2. квадрат: С = 2 * Р2;
3. шестерокут: С = (3√3) / 2 * Р2.

Ситуација са погрешном цифром

Алгоритам је начин за проналажење подручја полигона, ако није тачан и не може се приписати било којој од претходно познатих фигура:

• разделите га у једноставне облике, као што су троуглови, тако да се не укрштају;
• израчунајте њихову површину користећи било коју формулу;
• збројите све резултате.

Шта да радимо ако су координате тачака полигона дате у проблему?

То значи да је за сваку тачку познат низ парова бројева који ограничавају стране фигуре. Обично се пишу као (к ₁ ; и ₁ ) за први, (к ₂ ; и ₂ ) за други, а н-ти врх има ове вриједности (к _н ; и _н ). Тада се површина полигона дефинише као сума н појмова. Сваки од њих изгледа овако: ((и _{и + 1} + и _и ) / 2) * (к _{и + 1} - к _и ). У овом изразу, и варира од једног до н.

Треба напоменути да ће знак резултата зависити од заобилажења облика. Када користите наведену формулу и крећете се у смеру казаљке на сату, одговор ће бити негативан.

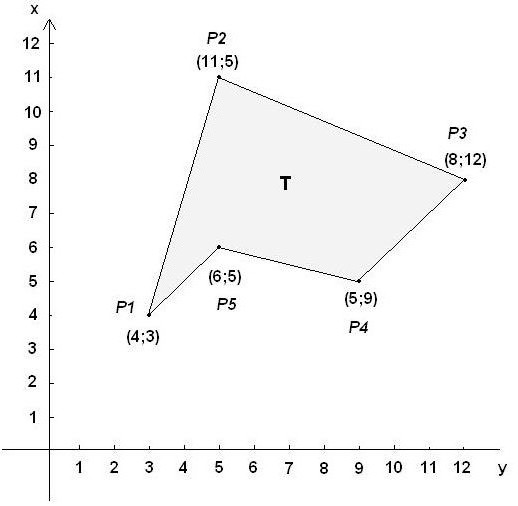
Пример задатка

Цондитион Координате врхова су дате вредностима (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Потребно је израчунати површину полигона.

Одлука. Према горњој формули, први термин ће бити (1.8 + 0.6) / 2 * (3.6 - 2.1). Овдје само требате узети вриједности за игру и Кс из другог и првог бода. Једноставан израчун ће довести до резултата 1.8.

Други термин је слично добивен: (2.2 + 1.8) / 2 * (2.3 - 3.6) = -2.6. При рјешавању таквих проблема немојте се бојати негативних вриједности. Све иде како треба. Ово је планирано.

Слично томе, вредности су добијене за трећи (0,29), четврти (-6,365) и пети (2,96). Тада је укупна површина: 1.8 + (-2.6) + 0.29 + (-6.365) + 2.96 = - 3.915.

Савет за решавање проблема за који је полигон приказан на папиру у ћелији

Најчешће је збуњујуће да је у подацима присутна само величина ћелије. Али испада да више информација није потребно. Препорука за решавање овог проблема је подела облика на много троуглова и правоугаоника. Њихова област је прилично једноставна за пребројавање дужине, које се затим лако савијају.

Али често постоји једноставнији приступ. Састоји се од цртања фигуре у правоугаоник и израчунавања вредности њене површине. Затим пребројите подручја оних елемената који су сувишни. Одузмите их од укупног износа. Ова опција понекад укључује нешто мањи број акција.