Како пронаћи хипотенузу: 4 начина за проналажење одговора

Након проучавања теме ригхт трианглес ученици често одбацују све информације о њима. Укључујући и како пронаћи хипотенузу, да не спомињемо шта је то.

И узалуд. Зато што се касније испостави да је дијагонала правоугаоника управо та хипотенуза и она се мора наћи. Ор пречник круга подудара се са највећом страном троугла, чији је један угао раван. И пронаћи га без овог знања је немогуће.

Постоји неколико опција за проналажење хипотенузе троугла. Избор методе зависи од почетног скупа података у исказу вредности проблема.

Метод број 1: оба су дата

Ово је најупечатљивији метод, јер се користи Питагорина теорема. Само понекад студенти забораве да је ова формула квадрат хипотенузе. Дакле, да бисте пронашли саму страну, морате извући скуаре роот. Дакле, формула за хипотенузу, која се обично означава словом "ц", ће изгледати овако:

ц = √ ( ² + у ² ) , где су ^два слова правог троугла написана словима “а” и “б”.

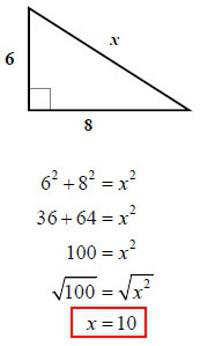
Метода број 2: Позната је ногу и угао који се налази поред њега

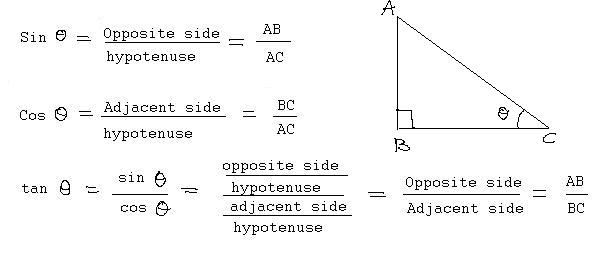
Да бисте сазнали како пронаћи хипотенузу, морат ћете се сјетити тригонометријских функција. Наиме, косинус. За практичност, претпостављамо да је дата нога "а" и угао а који се налази поред њега.

Сада треба да запамтимо да је косинус угла правоугаоног троугла једнак односу две стране. Нумератор ће бити вредност ногу, а именилац - хипотенуза. Из овога следи да се ово друго може рачунати по формули:

ц = а / цос α .

Начин број 3: дати ногу и угао који лежи насупрот њему

Да не бисмо били збуњени у формулама, уносимо нотацију за овај угао - β и остављамо страну као прије “а”. У овом случају, потребна је друга тригонометријска функција, синус.

Као у претходном примеру, синус је једнак односу ноге на хипотенузу. Формула за овај метод је следећа:

ц = а / син β .

Да се ​​не упетљате у тригонометријске функције, можете се сјетити једноставног мнемоничког правила: ако се проблем бави супротним углом, онда морате користити с и нус, ако се ради о пр и лагању, онда о синусу. Пажњу треба посветити првим самогласницима кључних речи. Они формирају парове о-и или -о .

Метод број 4: дуж обима кружнице

Сада, да бисмо научили како пронаћи хипотенузу, морамо се присјетити својства круга, који је описан око правог трокута. Она гласи како слиједи. Центар круга се поклапа са средином хипотенузе. Другим ријечима, највећа страна правог трокута је дијагонала круга. То је двоструки радијус. Формула за овај задатак ће изгледати овако:

ц = 2 * р , где је р познати радијус.

То су сви могући начини проналажења хипотенузе правог троугла. Да бисте користили у сваком конкретном задатку потребан вам је метод који је прикладнији за скуп података.

Пример проблема број 1

Услов: у правом троуглу, медијан се привлачи на обе ноге. Дужина оне која се држи на већој страни је .52. Други медијан је дуг 73 лонг. Потребно је израчунати хипотенузу.

Одлука.

Пошто су медијани нацртани у троуглу, ноге деле на два једнака сегмента. Због практичности, расуђивања и проналажења како пронаћи хипотенузу, потребно је да унесете неколико симбола. Нека обе половине већег катетуса буду означене словом “к”, а друга “и”.

Сада треба да размотримо два десна троугла, од којих су хипотенусе познати медијани. За њих морате писати два пута Формула Питагорина теорема :

(2и) ² + к ² = ()52) ²

и

(и) ² + (2к) ² = ()73) ² .

Ове две једначине формирају систем са две непознате. Након што их ријешимо, биће лако пронаћи ноге оригиналног троугла и, према њима, његову хипотенузу.

Прво морате изградити све до другог степена. Испада:

4и ² + к ² = 52

и

на ² + 4к ² = 73.

Из друге једначине може се видети да је ² = 73 - 4к ² . Овај израз мора бити замењен у први и израчунати "к":

4 (73 - 4к ² ) + к ² = 52.

Након конверзије:

292 - 16 к ² + к ² = 52 или 15 к ² = 240.

Из последњег израза к = =16 = 4.

Сада можете израчунати "и":

и ² = 73 - 4 (4) ² = 73 - 64 = 9.

и = 3.

Према стању, испоставља се да су ноге оригиналног троугла 6 и 8. Према томе, можете користити формулу из прве методе и пронаћи хипотенузу:

6 (6 ² + 8 ² ) = √ (36 + 64) = =100 = 10.

Одговор : хипотенуза је 10.

Пример задатка 2

Услов: израчунајте дијагоналу нацртану у правоугаонику са мањом страном која је једнака 41. Ако је познато да подели угао са онима који се односе као 2 на 1.

Одлука.

У овом задатку, дијагонала правоугаоника је највећа страна у троуглу са углом од 90º. Дакле, све се своди на то како пронаћи хипотенузу.

Проблем је у угловима. То значи да ћете морати да користите једну од формула у којој постоје тригонометријске функције. И прво морате одредити вредност једног од оштрих углова.

Нека је мањи од углова на које се односи услов α. Тада ће десни угао, који је подељен дијагоналом, бити једнак 3α. Математичка нотација за ово је:

90º = 3 α.

Из ове једначине једноставно одредите α. Биће једнако 30º. И она ће се налазити насупрот мањој страни правоугаоника. Стога вам је потребна формула описана у методи број 3.

Хипотенуза је једнака односу ноге на синус супротног угла, то јест:

41 / син 30º = 41 / (0.5) = 82.

Одговор: хипотенуза је 82.