Како ријешити судоку: начине, методе и стратегију

Судоку је математичка слагалица, родно мјесто које се сматра земљом излазећег сунца - Јапан. Време је за невероватно узбудљиву и развојну мистерију која пролази неопажено. У чланку ће се дати начини, методе и стратегија за решавање судокуа.

Историја имена игре

Чудно је да Јапан није мјесто рођења игре. У ствари, загонетку је измислио познати математичар Леонард Еулер у КСВИИИ веку. Од курса из виших математика, многи би требали запамтити познате “Еулер кругове”. Научник је био фасциниран комбинаторичким и пропозиционим логичким подручјима, он је своје квадрате различитих редова назвао "латински" и "грчко-латински", јер је углавном користио писма. Али права популарност слагалице стекла је након редовног објављивања у јапанском магазину Николи, гдје је 1986. године добила име Судоку.

Како изгледа мистерија?

Слагалица је квадратно поље са димензијама од 9 до 9 ћелија. У зависности од сложености и врсте слагалице, рачунар напушта одређени број квадрата. Понекад су почетници заинтересовани за питање: "Колико опција слагалице можете направити?".

Према правилима комбинатора, број пермутација се може наћи израчунавањем факторијала броја елемената. Дакле, судоку користи бројеве од 1 до 9, тако да је потребно израчунати факторијални 9. = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 7 * 9 = 362 880 - варијанте разних комбинација низова. Затим требате користити матрицну формулу пермутације и бројати могуће позиције редова и колона. Формула за израчунавање је прилично компликована, довољно је напоменути да ако замијените само у три ступца / реда, можете повећати укупан број опција за 6 пута. Множењем вредности добијамо 46 656 начина пермутација у матрици загонетки за само 1 комбинацију. Није тешко претпоставити да ће коначни број бити једнак 362.880 * 46.656 = 16.930.529.280 опција игре - на вама је да не одлучујете.

Међутим, према прорачунима Бертхам Фелгенхауера, слагалица има много више рјешења. Бертхамове формуле су веома сложене, али дају укупан број пермутација од 6,670,903,752,021,072,936,960 варијанти.

Правила игре

Правила игре судоку се разликују у зависности од врсте слагалице. Али за све варијације, захтеви класичног судоку су уобичајени: бројеви од 1 до 9 не би требало да се понављају вертикално и хоризонтално, као и на свакој означеној области "три по три".

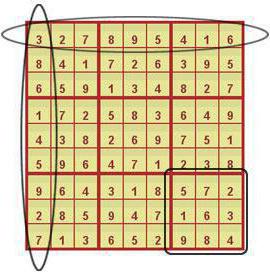
Постоје и друге врсте игара, као што су судоку, дијагонала, виндоку, гирандол, регион и латински судоку. На латинском језику, слова се користе умјесто бројева латиница. Чак и неуобичајена варијанта треба да буде решена као уобичајени судоку, узимајући у обзир само вишебојна подручја. У ћелијама исте боје треба да буду парни бројеви, а други - непарни. У дијагоналној загонетки према класичним правилима "вертикална, хоризонтална, три по три" додају се још два дијагонална поља, у којима не би требало бити ни понављања. Варијација региона је врста боје судоку, у којој нема три до три поделе класичног типа игре. Уместо тога, коришћењем боја или уљаних граница, бирају се произвољне области од 9 ћелија, у које се убацују бројеви.

Како исправно ријешити судоку?

Главно правило слагалице је: постоји само једна исправна цифра за сваку ћелију поља. Ако одаберете погрешан број у некој фази, даљње рјешење ће бити немогуће. Бројеви на вертикалној и хоризонталној ће почети да се понављају.

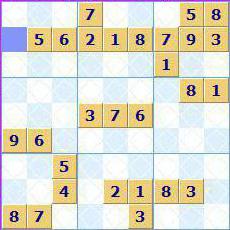
Најједноставнији примјер изјаве је ситуација с 8 познатих бројева хоризонтално, вертикално или у подручју "три по три". Начини решавања судокуа у овом случају су очигледни - унесите недостајућу цифру низа од 1 до 9 у жељени квадрат.У примеру на слици изнад, то ће бити број 4.

Понекад две ћелије "три по три" остају неиспуњене. У овом случају, свака ћелија има две могућности попуњавања, али само једна је исправна. Прави избор можете направити тако што ћете размотрити празна подручја не само као дио подручја, већ и као дио вертикалне и хоризонталне. На пример, у квадрату "три по три" нема довољно 2 и 3. Потребно је изабрати једну ћелију и узети у обзир вертикално и хоризонтално укрштање које је. Претпоставимо да је већ три вертикално, али у обе секвенце нема довољно 2. Онда је избор очигледан.

Загонетке на почетном нивоу су тешке, по правилу пружају могућност да се одмах попуне неколико ћелија са само исправним вредностима. Потребно је само пажљиво размотрити игралиште. Али није увијек избор начина / метода како ријешити судоку тако једноставан.

Шта значи “предефинисани избор” у судоку?

Понекад избор није једини, већ је ипак предодређен. Назовимо такав број "јединственим кандидатом". Проналажење таквог распореда бројева на пољу слагалице је лако, али ће захтевати неко искуство у решавању загонетке. Пример како правилно решити судоку са јединственим кандидатом детаљно је описан за варијацију игралишта на слици испод.

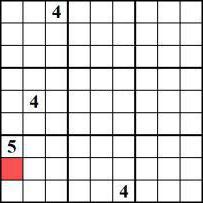
На означеном црвеном квадрату, на први поглед, може стајати било који број, осим 5. Међутим, у ствари, јединствени кандидат за место је број 4. Неопходно је узети у обзир све вертикале и хоризонтале разматраног подручја “три по три”. Дакле, у вертикалама 2 и 3 постоје четворке, што значи да 4 мала поља могу бити у једном од три квадрата прве колоне. Горњи квадрат је већ заузет бројем 5, број локација симбола 4 је смањен. У доњем хоризонту подручја такође није тешко наћи четири, дакле, од 3 варијанте локације броја, само један остаје.

Потражите јединственог кандидата на терену

Разматрани пример је био очигледан, јер једноставно није било других бројева на терену. Проналажење јединственог кандидата у одређеној слагалици није лако. Игралиште на слици испод ће послужити као јасан примјер за објашњење начина како ријешити судоку трагајући за јединственим кандидатом.

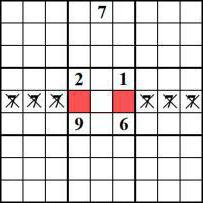
Иако се опис рјешења не чини једноставним, његова примјена у пракси није тешка. Јединственог кандидата се увијек тражи у специфичном подручју од три по три. У том смислу, играча занимају само три вертикале и три хоризонтале игралишта. Сви други се сматрају неважним и једноставно одбачени. У примјеру је потребно пронаћи мјесто јединственог кандидата број 7 за централни регион. Угаони квадрати разматраног поља су заузети бројевима, а број 7 је већ присутан у централној вертикали, што значи да су једини могући квадрати за постављање јединственог кандидата 7 прва и трећа ћелија средњег реда три по три области.

Како ријешити тешки судоку?

У свакој врсти игре подијељене су 4 разине тежине. Они се разликују по броју цифара у почетној верзији поља. Што их је више, лакше је ријешити судоку. Као иу другим играма, навијачи организују такмичења и читава судоку првенства.

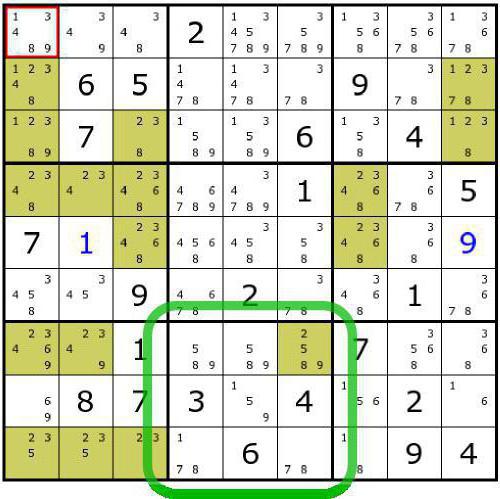
Најтеже варијанте игре укључују велики број опција за попуњавање сваке ћелије. Понекад могу бити максимални могући број - 8 или 9. У таквим ситуацијама, препоруча се да се оловком запишу све опције око ивица и углова кавеза. Набрајање свих комбинација, уз детаљну студију, већ може помоћи да се елиминишу пресечени бројеви и смањи број варијација за једну ћелију.

Стратегије боја за решавање загонетке

Тежа верзија игре су судоку загонетке са бојом. Тешке загонетке се разматрају због увођења додатних услова. У ствари, боја није само елемент компликација, већ и врста наговјештаја, који се у одлуци не смије занемарити. Ово важи и за игру чак и непарних.

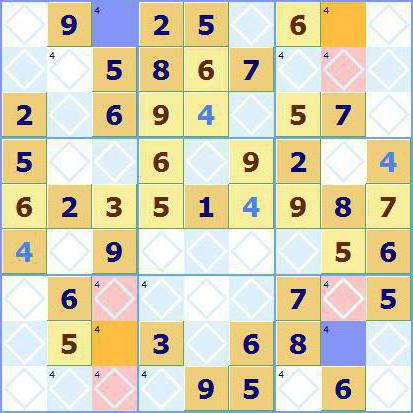
Али боја се такође може користити за решавање обичног судоку, уз напомену о вероватнијим случајевима замене. У горњој слици слагалице, слика 4 се може ставити само у плаве и наранчасте ћелије, све остале опције су очигледно погрешне. Одабиром одређених подручја омогућит ћете да се одвратите од броја 4 и пребаците се на тражење других вриједности, док заборављање на ћелије неће радити.

Судоку за децу

Ово може звучати чудно, али деца воле да решавају судоку. Игра је врло добро развијена логика и маштовито размишљање. Научници су већ доказали да игра спречава смрт можданих ћелија. Људи који редовно решавају загонетку имају виши ИК ниво.

За веома малу децу која још не знају бројеве, развијене су судоку варијанте са симболима. Загонетка је апсолутно семантички независна. Родитељи би свакако требали научити дјецу да играју судоку ако желе развити логику, концентрацију и размишљање дјеце. Игра је корисна за одржавање менталних способности у било ком узрасту. Истраживачи упоређују акцију слагалице са људским мозгом са ефектом физичких вежби за развој мишића. Психолози тврде да судоку ублажава депресију и помаже у лечењу деменције.