Механичка енергија и њени типови

Сврха овог чланка је да открије суштину концепта "механичке енергије". Физика широко користи овај концепт и практично и теоретски.

Рад и енергија

Механички рад се може одредити ако је позната сила која делује на тело и кретање тела. Постоји још један начин израчунавања механичког рада. Размотрите пример:

Слика приказује тело које може бити у различитим механичким стањима (И и ИИ). Процес транзиције тела из стања И у стање ИИ карактерише механички рад, тј. Када се креће од стања И до стања ИИ, тело може обављати посао. Приликом извођења посла, механичко стање тела се мења, а механичко стање може се карактерисати једном физичком количином - енергијом.

Енергија је скаларна физичка величина свих облика кретања материје и варијанти њихове интеракције.

Шта је механичка енергија

Механичка енергија је скаларна физичка величина која одређује способност тела да обавља посао.

А = .Е

Пошто је енергија карактеристика стања система у одређеном тренутку, рад је карактеристика процеса промене стања система.

Енергија и рад имају исте јединице: [А] = [Е] = 1 Ј.

Типови механичке енергије

Механичка слободна енергија се дели на два типа: кинетички и потенцијални.

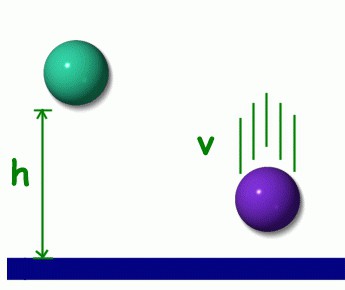
Кинетичка енергија је механичка енергија тела, која се одређује брзином његовог кретања.

Е _к = 1 / 2мв ²

Кинетичка енергија је својствена покретним телима. Заустављају се, обављају механички рад.

У различитим референтним системима, брзине истог тела у произвољном тренутку могу бити различите. Према томе, кинетичка енергија је релативна вредност, она се одређује избором референтног система.

Ако сила делује на тело током кретања (или неколико сила истовремено), кинетичка енергија тела се мења: тело убрзава или зауставља. Истовремено, рад силе или рад резултанта свих сила које се примењују на тело биће једнак разлици кинетичких енергија:

А = Е _к1 - Е _{к 2} = ΔЕ _к

Овој тврдњи и формули дат је назив - теорема кинетичке енергије .

Потенцијална енергија се назива енергија због интеракције између тијела.

Када тело масе м падне са висине х, снага привлачења обавља посао. Пошто су рад и промена енергије повезани једначином, може се написати формула за потенцијалну енергију тела у пољу гравитација :

Е _п = мгх

За разлику од кинетичке енергије Е _к, потенцијал Е _п може имати негативну вриједност када је х <0 (на примјер, тијело лежи на дну бунара).

Друга врста механичке потенцијалне енергије је енергија деформације. Опруга компримирана на удаљености к са крутошћу к има потенцијалну енергију (енергију деформације):

Е _п = 1/2 кк ²

Енергетска деформација је нашла широку примјену у пракси (играчке), у техници - стројевима, релејима и др.

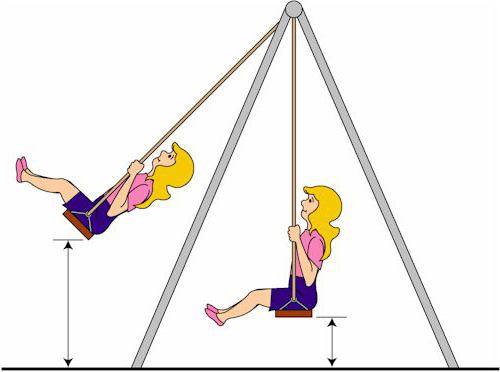
Е = Е _п + Е _к

Укупна механичка енергија тела се назива сума енергија: кинетичка и потенцијална.

Закон очувања механичке енергије

Један од најпрецизнијих експеримената које су енглески физичар Јоуле и немачки физичар Маиер спровели средином 19. века показали су да количина енергије у затвореним системима остаје непромењена. Она се само креће од једног до другог тијела. Ове студије су помогле да се открије закон очувања енергије :

Укупна механичка енергија изолованог система тела остаје константна за све интеракције тела међу собом.

За разлику од импулса, који нема еквивалентну форму, енергија има многе облике: механичку, топлотну, енергију молекуларног кретања, електричну енергију са силама интеракције набоја и друге. Један облик енергије се може пренијети на други, на примјер, топлинска кинетичка енергија се преноси у процесу кочења аутомобила. Ако силе трења не, и топлота се не генерише, онда се укупна механичка енергија не губи, већ остаје константна током кретања или интеракције тела:

Е = Е _п + Е _к = конст

Када је сила трења између тела, онда долази до смањења механичке енергије, међутим, у овом случају, она се не губи без трага и прелази у топлоту (унутрашњу). Ако спољна сила врши рад на затвореном систему, онда долази до повећања механичке енергије за количину рада коју ова сила обавља. Ако затворени систем обавља рад на вањским тијелима, тада се механичка енергија сустава смањује количином посла који је обавио.
Свака врста енергије може се потпуно претворити у било коју другу врсту енергије.