Неинертни референтни оквир: дефиниција, примјери
Сви референтни системи су подељени на инерцијалне и не-инерцијалне. Инертни референтни оквир лежи у Невтоновој механици. Карактерише га једнолично правоцртно кретање и стање мировања. Неинертни референтни оквир је повезан са убрзаним кретањем дуж различите путање. Ово кретање је дефинисано у односу на инерцијалне референтне системе. Неинертни референтни систем је повезан са ефектима као што су инерцијална сила, центрифугална сила и Цориолисова сила.
Сви ови процеси настају као резултат кретања, а не интеракције између тијела. Њутнови закони у не-инерцијалним референтним системима често не функционишу. У таквим случајевима, амандмани се додају класичним законима механике. Силе због неинертног кретања узимају се у обзир при развоју техничких производа и механизама, укључујући и оне у којима је ротација присутна. У животу их сусрећемо, крећемо се у лифту, возимо се на вртуљку, гледамо вријеме и ток ријека. Они се узимају у обзир при израчунавању кретања летилице.
Ad

Инерцијални и не-инерцијални референтни системи
Инерцијални референтни системи нису увек погодни за описивање кретања тела. У физици постоје два типа референтних система: инерцијални и не-инерцијални референтни системи. Према механици Њутна, свако тело може бити у стању мировања или униформног и праволинијског кретања, осим у случајевима када се спољашњи утицај врши на тело. Такво једнообразно кретање назива се инерцијално кретање.
Инерцијални покрет (инерцијални референтни системи) је основа Невтонове механике и Галилејевих радова. Ако се звезде сматрају фиксним објектима (што уствари није сасвим случај), онда ће се сви објекти који се крећу у односу на њих равномерно и директно обликовати инерцијалне референтне системе.
Ad

За разлику од инерцијалних референтних система, не-инерцијални систем се креће у односу на специфицирани са одређеним убрзањем. У овом случају, употреба Невтонових закона захтева додатне варијабле, иначе ће неадекватно описати систем. Да би се одговорило на питање, који се референтни системи називају не-инерцијалним, вреди размотрити пример неинертијалног покрета. Овај покрет је ротација наших и других планета.
Кретање у не-инерцијалним референтним системима
Коперник је био први који је показао колико је тешко кретање ако у њему учествује неколико сила. Пре њега се веровало да се Земља креће сама по себи, у складу са Њутновим законима, па је њено кретање инерцијално. Међутим, Коперник је доказао да се Земља окреће око Сунца, то јест, ради убрзано кретање у односу на условно стационарни објекат, који звезда може бити.
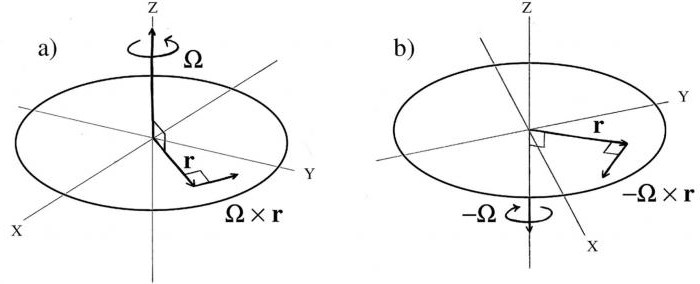
Дакле, постоје различити референтни системи. Неинертни називају само онима у којима постоји убрзано кретање, које је дефинисано у односу на инерцијални систем.
Земља као референтни систем
Не-инерцијални референтни оквир, примјери чије се постојање може наћи готово свуда, типичан је за тијела са сложеном путањом кретања. Земља се окреће око Сунца, што ствара карактеристику убрзаног кретања неинертних референтних система. Међутим, у свакодневној пракси, све што сусрећемо на Земљи је сасвим у складу с Невтоновим постулатима. Ствар је у томе да су корекције не-инерцијалних кретања за референтне системе везане за Земљу веома мале и не играју велику улогу за нас. А Невтонове једначине из истог разлога испадају генерално поштене.
Ad

Фоуцаултов Пендулум
Међутим, у неким случајевима није потребна никаква измјена. На пример, светски Фоуцаулт клатно у катедрали у Санкт Петербургу не само да врши линеарне осцилације, већ се и полако окреће. Ова ротација је узрокована не-инерцијалним кретањем Земље у свемиру.
Први пут је то постало познато 1851. године након експеримента француског научника Л. Фоуцаулта. Сам експеримент није спроведен у Петрограду, већ у Паризу, у великој дворани. Тежина куглице клатна је била око 30 кг, а дужина спојног навоја била је чак 67 метара.
У оним случајевима када само Невтонове формуле за инерцијални референтни оквир нису довољне да опишу кретање, оне додају такозване силе инерције.
Својства неинертног референтног система
Не-инерцијални референтни систем обавља различите покрете у односу на инерцијални. Може бити кретање напред ротација, сложени комбиновани покрети. У литератури је дат и најједноставнији пример неинертног референтног система, као што је лифт са убрзаним кретањем. Управо због његовог убрзаног кретања осећамо како смо притиснути на под, или, напротив, сензација је близу бестежинском стању. Невтонови закони механике не могу објаснити овај феномен. Ако пратите чувеног физичара, онда ће у сваком тренутку иста сила гравитације деловати на особу у лифту, што значи да сензације треба да буду исте, али у стварности све је другачије. Дакле, према законима Њутна, морате додати додатну силу, која се зове сила инерције.
Ad
Инерција
Сила инерције је реална сила дјеловања, иако се по природи разликује од сила које су повезане са интеракцијом између тијела у простору. Она се узима у обзир у развоју техничких структура и апарата и игра важну улогу у њиховом раду. Силе инерције се мере на различите начине, на пример, коришћењем динамометра. Не-инерцијални референтни системи нису затворени, јер се силе инерције сматрају вањским. Снаге инерције су објективни физички фактори и не зависе од воље и мишљења посматрача.
Инерцијални и не-инерцијални референтни системи, примјери којих се могу наћи у уџбеницима физике, су дјеловање инерцијске силе, центрифугалне силе, Цориолисове силе, пријенос момента из једног тијела у друго и друге.

Покрет у лифту
Неинертни референтни системи, инерцијалне силе добро се манифестују током убрзаног успона или спуштања. Ако се дизало креће нагоре са убрзањем, тада резултирајућа инерцијална сила тежи да притиска особу на под, а када кочи, тело, напротив, почиње да изгледа лакше. У смислу манифестација, сила инерције у овом случају је слична гравитација али има веома различиту природу. Гравитација је гравитација, која је повезана са интеракцијом између тела.
Ad

Центрифугална сила
Силе у не-инерцијалним референтним системима могу бити центрифугалне. Потребно је увести такву силу из истог разлога као и сила инерције. Живописан пример дејства центрифугалних сила - ротације на вртуљку. Док столица настоји да задржи особу у њеној "орбити", сила инерције узрокује да тијело притисне према вањској стражњој страни столице. Ова конфронтација се изражава појавом таквог феномена као што је центрифугална сила.
Цориолисова снага
Ефекат ове силе је добро познат из примера ротације Земље. Можете га назвати сила само условно, јер није. Суштина њеног деловања је да се током ротације (на пример, Земље) свака тачка сферног тела креће у круг, док се објекти отргнути од Земље идеално крећу равно (као тело које слободно лети у свемиру). Пошто је линија земљописне ширине путања ротације тачака на површини Земље, и има облик прстена, сва тела одвојена од ње и иницијално се крећу дуж ове линије, крећући се линеарно, почињу да се све више удаљавају од ње у правцу нижих географских ширина.
Друга опција је када се тело лансира у меридионалном правцу, али због ротације Земље, са становишта земаљског посматрача, кретање тела више неће бити стриктно меридионално.
Кориолисова сила има велики утицај на развој атмосферских процеса. Под његовим утицајем, вода удара у источну обалу река које тече у меридијалном правцу теже, постепено еродирајући, што доводи до појаве литица. Напротив, на западу се таложе падавине, тако да је током поплава њежније и често поплављено водом. Истина, то није једини разлог зашто је једна страна ријеке већа од друге, али у многим случајевима она је доминантна.
Цориолисова сила такође има експерименталне доказе. Добио га је немачки физичар Ф. Рајх. У експерименту су тијела пала са висине од 158 м. Укупно је изведено 106 таквих експеримената. Када је тело пало, они су одступали од равне (са тачке гледишта земаљског посматрача) путање за око 30 мм.
Инерцијални референтни системи и теорија релативности
Специјална теорија релативности Еинстеин је настао у односу на инерцијалне референтне системе. Такозвани релативистички ефекти, према овој теорији, требали би се појавити у случају врло великих брзина тијела у односу на "стационарни" посматрач. Све формуле посебне теорије релативности обојене су и за равномерно кретање, типично за инерцијални референтни систем. Први постулат ове теорије потврђује еквивалентност било којих инерцијалних референтних система, тј. Претпоставља се одсуство посебних, посвећених система.
Међутим, то доводи у питање могућност провјере релативистичких ефеката (као и саме чињенице њиховог постојања), што је довело до појаве таквих феномена као што је двоструки парадокс. Пошто су референтни системи повезани са ракетом и Земљом у основи једнаки у правима, онда ће ефекти временске дилатације у пару Земља-Ракета зависити само од тога где је посматрач. Дакле, за посматрача на ракети, вријеме на Земљи треба ићи спорије, а за особу на нашој планети, напротив, треба ићи спорије на ракету. Као резултат тога, близанац који остане на Земљи ће видјети свог брата који долази млађи, и онај који је био у ракети, након што је улетио, требао би видјети млађе од оног који је остао на Земљи. Јасно је да је ово физички немогуће.
Дакле, да бисмо посматрали релативистичке ефекте, потребна нам је нека врста посебног, посвећеног референтног оквира. На пример, претпоставља се да посматрамо релативистичко повећање животног века миона, ако се крећу брзином блиском светлости у односу на Земљу. То значи да Земља (штавише, без икакве алтернативе) посједује својства приоритетног, основног референтног система, што је у супротности са првим постулатом СРТ-а. Приоритет је могућ само ако је Земља центар универзума, што је конзистентно само са примитивном сликом свијета и супротно физици.
Не-инерцијални референтни системи као неуспјешан начин објашњавања двоструког парадокса
Покушаји да се објасни приоритет "земаљског" референтног оквира не држе воду. Неки научници овај приоритет приписују фактору инерције једног и не-инерцијалности другог референтног оквира. У овом случају, референтни систем повезан са посматрачем на Земљи сматра се инерцијалним, упркос чињеници да је у физичкој науци званично признат као не-инерцијални (Детлаф, Иаворски, курс физике, 2000). Ово је први. Други је исти принцип једнакости свих референтних система. Дакле, ако свемирска летелица напусти Земљу са убрзањем, онда са становишта посматрача на самом броду, она је статична, а Земља, напротив, одлеће од ње са све већом брзином.
Испоставља се да је сама Земља посебан референтни систем, или посматрани ефекти имају другачије (не-релативистичко) објашњење. Можда су процеси повезани са специфичностима формулације или интерпретације експеримената, или са другим физичким механизмима посматраних феномена.
Закључак
Дакле, не-инерцијални референтни системи доводе до појаве сила које нису нашле своје место у законима Невтонове механике. При обрачуну за не-инерцијалне системе, обрачунавање ових сила је обавезно, укључујући и развој техничких производа.