Паралакс је оно што је?

Космос је један од најтајанственијих концепата на свету. Ако гледате у небо ноћу, можете видјети безброј звијезда. Да, вероватно, свако од нас је чуо да има више звезда у Свемиру од зрна песка у Сахари. А научници из древних времена пружали су се на ноћно небо, покушавајући да реше загонетке скривене иза ове црне празнине. Од давнина имају побољшане методе за мерење раздаљине на простору и својства звездане материје (температура, густина, брзина ротације). У овом чланку ћемо говорити о томе шта је паралакса звезда и како се она користи у астрономији и астрофизици.

Феномен паралаксе је уско повезан са геометријом, али пре него што размотримо геометријске законе који леже у основи ове појаве, уронит ћемо у историју астрономије и испитати ко и када је открио ту особину кретања звезда и применио је у пракси.

Хистори оф

Паралакса као феномен промене положаја звезда у зависности од локације посматрача је позната већ дуже време. Више о томе је Галилео Галилео писао у далеком средњем вијеку. Он је само претпоставио да ако је могуће приметити промену паралаксе за удаљене звезде, то би био доказ Земља се окреће око Сунца, а не обрнуто. И то је истина. Међутим, Галилео то није могао доказати због недовољне осјетљивости тадашње опреме.

Ближе нашим данима, 1837. године, Василиј Јаковљевић Струве је спровео низ експеримената за мерење годишње паралаксе за звезду Вега, која се налази у сазвежђу Лира. Касније, ова мерења су сматрана непоузданим када је, у години након објављивања Струвеа, 1838, Фриедрицх Вилхелм Бессел измерио годишњу паралаксу за звезду 61 Цигнус. Стога, без обзира колико то било тужно, приоритет отварања једногодишњег паралакса још увијек припада Бесселу.

Данас се паралакс користи као главни метода мерења удаљености до звезда и са довољно прецизном мерном опремом даје резултате са минималном грешком.

Требало би да пређемо на геометрију пре него што директно узмемо у обзир паралаксу. И за почетак, запамтите саме основе овог занимљивог, иако незаслуженог од многих науке.

Основе геометрије

Дакле, оно што требамо знати из геометрије да бисмо разумјели феномен паралаксе је начин на који су углови између страна трокута и њихове дужине повезани.

За почетак, замислите троугао. Има три повезане равне линије и три угла. И за сваки други троугао - његове сопствене углове и дужине стране. Немогуће је променити величину једне или две стране троугла са константним вредностима углова између њих, то је једна од основних истина геометрије.

Замислите да се суочавамо са задатком да утврдимо вредност дужина двеју страна, ако знамо само дужину базе и величину углова који се налазе поред ње. То је могуће уз помоћ једне математичке формуле која повезује вриједности дужина страница и вриједности углова који леже насупрот њима. Замислите да имамо три врха (можете узети оловку и нацртати их) који чине троугао: А, Б, Ц. Они формирају три стране: АБ, БЦ, ЦА. Насупрот сваком од њих лежи угао: угао БЦА насупрот АБ, угао БАЦ наспрам БЦ, угао АБЦ наспрам ЦА.

Формула која повезује свих ових шест количина заједно изгледа овако:

АБ / син (БЦА) = БЦ / син (БАЦ) = ЦА / син (АБЦ).

Као што видимо, све није сасвим једноставно. Однекуд имамо синус од углова. Али како ћемо наћи овај синус? О томе ћемо рећи у наставку.

Основе тригонометрије

Синус је тригонометријска функција која одређује И координату угла на координатној равни. Да би се то јасно показало, обично цртају координатну раван са две осе - ОКС и ОИ - и означавају тачке 1 и -1 на свакој од њих. Ове тачке се налазе на истој удаљености од центра равни, па се кроз њих може извући круг. Дакле, имамо такозвани јединствени круг. Сада ћемо конструисати неки сегмент са почетком на почетку координата и крај у некој тачки нашег круга. Крај сегмента који лежи на кругу има одређене координате на оси ОКС и ОИ. Вредности ових координата ће бити косинус и синус.

Сазнали смо шта је синус и како га можете пронаћи. Али, у ствари, овај метод је чисто графички и креиран да схвати суштину тригонометријских функција. Може бити ефикасан за углове који немају бесконачне рационалне вредности косинуса и синуса. За ово друго, ефикаснији је други метод, који се заснива на употреби деривата и биномних калкулација. То се зове Таилорова серија. Овај метод нећемо разматрати јер је он компликован за рачунање. На крају крајева, брзо рачунање је рад за рачунаре који су дизајнирани за то. Таилорова серија се користи у калкулаторима за израчунавање многих функција, укључујући синус, косинус, логаритам и тако даље.

Све је ово веома занимљиво и заразно, али је време да наставимо даље и да се вратимо тамо где смо завршили: на задатку да израчунамо вредности непознатих страна троугла.

Стране троугла

Дакле, вратимо се на наш проблем: знамо два угла и страну троугла, којима су ови углови суседни. Морамо да знамо само један угао и две стране. Чини се да је проналажење кута најлакши: збир свих трију углова троугла је 180 степени, што значи да можете лако пронаћи трећи угао тако што ћете одузети вредности два позната угла од 180 степени. И знајући вредности сва три угла и једну од страна, могу се наћи дужине две друге стране. Можете то сами провјерити на примјеру било којег трокута.

А сада хајде да коначно говоримо о паралакси као о начину мерења растојања између звезда.

Параллак

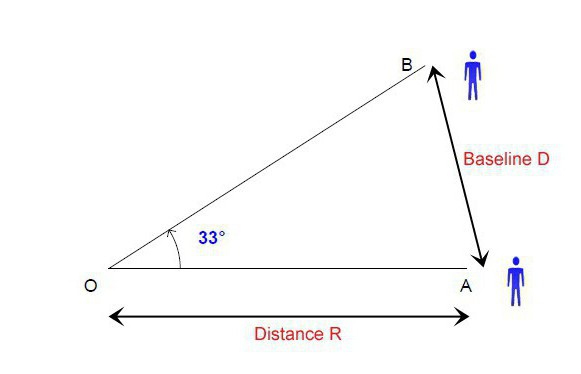
Ово је, као што смо већ сазнали, један од најједноставнијих и најефикаснијих метода за мерење међузвјезданих удаљености. Паралакса се заснива на промени положаја звезде у зависности од њене удаљености. На пример, мерењем угла привидне позиције звезде у једној тачки орбите, а затим директно од ње, добијамо троугао у коме је позната дужина једне стране (растојање између супротних тачака орбите) и два угла. Одавде ћемо моћи да пронађемо две преостале стране, од којих је свака једнака растојању од звезде до наше планете на различитим тачкама њене орбите. Ово је метод којим се може израчунати паралакса звезда. И не само звезде. Паралакс, чији је ефекат веома једноставан, упркос томе, користи се у многим његовим варијацијама у потпуно различитим областима.

У наредним одељцима детаљније ћемо размотрити опсег паралаксе.

Космос

О томе смо више пута разговарали, јер је паралакса изузетан изум астронома, дизајниран за мјерење удаљености до звијезда и других свемирских објеката. Међутим, то није тако једноставно. На крају крајева, паралакса је метода која има своје варијације. На пример, разликују се дневне, годишње и прастаре паралаксе. Може се претпоставити да се сви разликују у временском интервалу који пролази између корака мерења. Не може се рећи да повећање временског интервала повећава тачност мерења, јер циљеви сваког типа ове методе су различити, а тачност мерења зависи само од осетљивости опреме и одабране удаљености.

Даили параллак

Дневна паралакса, удаљеност којом се одређује кут између линија које иду до звијезде из двије различите точке: средиште Земље и одабрана точка на Земљи. Пошто знамо полупречник наше планете, није тешко, користећи угловну паралаксу, израчунати удаљеност до звезде, користећи математички метод који смо раније описали. У основи, дневна паралакса се користи за мерење близу објеката, као што је планете, патуљасти планети или астероиди. За већу употребу користите следећу методу.

Паралакса од годину дана

Једногодишња паралакса је још увијек иста метода мјерења удаљености с једином разликом што се фокусира на мјерење удаљености до звијезда. То је управо случај паралаксе који смо размотрили у горњем примјеру. Паралакса, одређивање удаљености до звезде чија помоћ може бити сасвим тачна, треба да има једну важну карактеристику: удаљеност од које се мери паралакса треба да буде већа, то боље. Једногодишња паралакса задовољава овај услов: ипак, растојање између екстремних тачака орбите је прилично велико.

Паралаксе, примјери метода које смо разматрали, свакако је важан дио астрономије и служи као незамјењив алат у мјерењу удаљености до звијезда. У ствари, данас се користи само једна година паралаксе, јер се дневна може заменити напреднијом и бржом ехолокацијом.

Само напред. Паралакс је још увек оптички феномен, и било би чудно да се његове особине користе само у астрономији. Постоји још једна област примене овог ефекта.

Пхотограпхи

Можда најпознатија врста фотографске паралаксе може бити бинокуларна паралакса. Вероватно сте то и сами приметили. Ако прстом доведете очи и затворите свако око, приметићете да се промени угао гледања објекта. Иста ствар се дешава када снимате блиске објекте. У објективу видимо слику из једног угла, али у ствари фотографија ће изаћи са мало другачијим углом, будући да постоји разлика у удаљености између сочива и тражила (рупа кроз коју гледамо фотографију).

Пре него што завршимо овај чланак - неколико речи о томе како таква појава као што је оптичка паралакса може бити корисна, и зашто бисте требали сазнати више о томе.

Зашто је то занимљиво?

За почетак, паралакса је јединствен физички феномен, који нам омогућава да научимо много о свету око нас, па чак ио томе шта је у стотинама лигхт иеарс од њега: након свега, уз помоћ овог феномена могуће је израчунати величине звијезда.

Као што смо већ видели, паралакса није толико удаљена појава од нас, она нас окружује свуда, и уз помоћ ње ми видимо како је. Ово је свакако занимљиво и узбудљиво, и зато треба обратити пажњу на метод паралаксе, макар само из радозналости. Знање никада није сувишно.

Закључак

Дакле, анализирали смо суштину паралаксе, зашто одредити удаљеност од звијезда није потребно имати сложену опрему, већ само телескоп и знање о геометрији, како се користи у нашем тијелу и зашто можемо бити толико важни у свакодневном животу. Надамо се да су вам информације биле корисне!