Волумен паралелепипеда: основне формуле и примјери задатака
Често се студенти огорчено питају: "Како то могу користити у животу?" О било којој теми сваког субјекта. Питање волумена паралелепипеда није изузетак. И овде можете само рећи: "То је корисно."
Како, на пример, сазнати да ли ће се пакет уклопити у поштанску кутију? Наравно, могуће је пробним и погрешним одабиром одговарајућег. А ако не постоји таква могућност? Онда ће доћи до спашавања. Знајући капацитет кутије, можете израчунати волумен пакета (барем приближно) и одговорити на постављено питање.
Параллелепипед и његови типови
Ако дословно преведете његово име са старогрчког, испада да је то фигура која се састоји од паралелних равни. Постоје такве еквивалентне дефиниције паралелепипеда:
- призма са базом у облику паралелограма;
- полиедар, од којих је свако лице паралелограм.
Њени типови се разликују у зависности од тога која фигура лежи у бази и како су бочне ивице усмерене. Генерално говоре о нагнутом паралелопипеду , чија је основа и сва лица паралелограми. Ако, у претходном приказу, бочна лица постану правоугаоници, онда ће то бити потребно назвати правим линијама . И правоугаона база такође има углове од 90º.
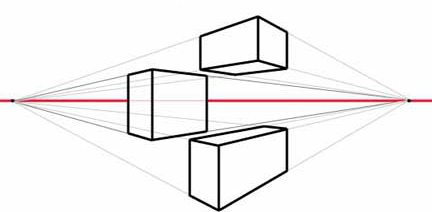
И други у геометрији покушавају да прикажу тако да је приметно да су све ивице паралелне. Овдје се, узгред, уочава главна разлика између математичара и умјетника. Најзад, важно је пренијети тијело уз поштивање закона о проспекту. У овом случају паралелност ребара је потпуно невидљива.
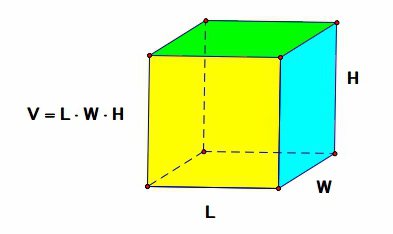
О унетој нотацији
У доњим формулама, нотација у табели је важећа.
| Магнитуде | Његова ознака |
| дужине основног руба | а |
| дужина бочног ребра | са |
| висина | н |
| основна област | С о |
| страна површине | С б |
| укупна површина | С п |
| основни периметар | Р о |
| волумен | В |
Формуле за косо паралелепипед
Први и други за простор:
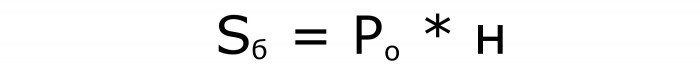
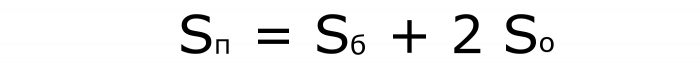
Трећи да би се израчунао обим паралелепипеда:

Будући да је база паралелограм, да бисте израчунали његову површину, морате користити одговарајуће изразе.
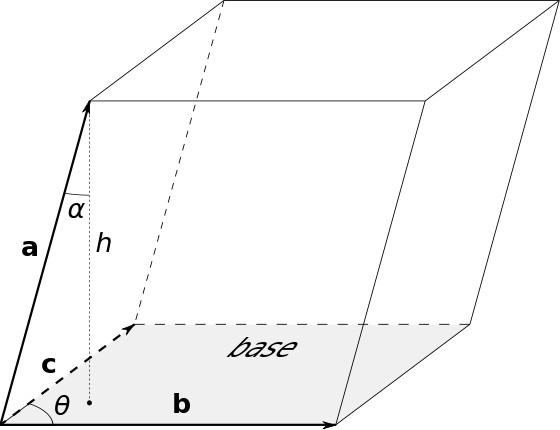
Формуле за правоугаони паралелепипед
Слично као и прва ставка - две формуле за области:
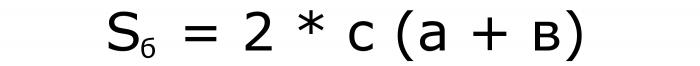
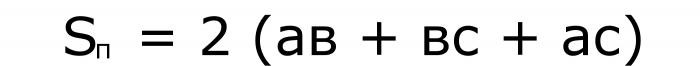
И још једна за волумен:

Први задатак
Цондитион Даје се правоугаони паралелепипед, чији волумен желите да пронађете. Позната дијагонала - 18 цм - и чињеница да формира углове од 30 и 45 степени са равнином бочне стране и бочне ивице, респективно.
Одлука. Да бисте одговорили на питање проблема, морате знати све стране у три ригхт трианглес. Они ће дати потребне вриједности рубова, које треба рачунати на волумен.
Прво треба да сазнате где је угао на 30º. Да бисте то урадили, морате нацртати дијагоналу бочне стране из истог врха из којег је извлачена главна дијагонала паралелограма. Угао између њих биће оно што је потребно.
Први троугао, који ће дати једну од вредности страна базе, биће следећи. Садржи жељену страну и два дијагонално постављена. Правоугаони је. Сада морате користити однос супротне стране (базне стране) и хипотенузе (дијагонално). Он је једнак синусу од 30º. То значи да ће непозната страна базе бити дефинисана као дијагонала помножена са синусом од 30º или ½. Нека буде означено словом “а”.
Лако се броји: а = 18 * ½ = 9 (цм).
Други ће бити троугао који садржи познату дијагоналу и ивицу са којом формира 45º. Такође је правоугаоног облика и можете поново користити однос ногу према хипотенузи. Другим речима, бочна ивица до дијагонале. Он је једнак косинусу од 45º. То јест, "ц" се рачуна као производ дијагонале од косинуса од 45º.
ц = 18 * 1 / =2 = 9 (2 (цм).
У истом троуглу потребно је пронаћи другу ногу. То је неопходно да би се треће непознато - "у" пребројило. Нека буде означено словом "к". Лако је израчунати по Питагориној теореми:
к = √ (18 2 - (9√2) 2 ) = 9√2 (цм).
Сада треба да размотримо други правоугаони троугао. Садржи већ познате стране "с", "к" и оне које требате рачунати, "ц":
ц = √ ((9√2) 2 - 9 2 = 9 (цм).
Све три количине су познате. Можете користити формулу за волумен и бројати је:
В = 9 * 9 * 9√2 = 729к2 (цм3).
Одговор: волумен паралелепипеда је 729к2 цм3.
Други задатак
Цондитион Потребно је наћи волумен паралелепипеда. Познате су стране паралелограма, који лежи на дну, 3 и 6 цм, као и његов оштар угао - 45º. Бочна ивица има нагиб до базе од 30º и износи 4 цм.
Одлука. Да бисте одговорили на питање проблема, морате узети формулу која је написана за волумен нагнутог паралелопипеда. Али у њему су обје количине непознате.
Подручје базе, тј. Паралелограм, одређује се по формули у којој морате помножити познате стране и синус акутног угла између њих.
С о = 3 * 6 син 45º = 18 * ()2) / 2 = 9 ( 2 (цм 2 ).
Друга непознаница је висина. Може се извући из било које од четири врха изнад базе. Налази се из правоугаоног троугла, у коме је висина нога, а бочна ивица је хипотенуза. Угао од 30º лежи насупрот непознатој висини. Дакле, можете користити став ногу према хипотенузи.
н = 4 * син 30º = 4 * 1/2 = 2.
Сада су све вриједности познате и можете израчунати волумен:
В = 9 *2 * 2 = 18 (2 (цм3).
Одговор: волумен је 18 × 2 цм3.
Трећи задатак
Цондитион Пронађите волумен паралелепипеда, ако знате да је раван. На бочним странама подножја формира се паралелограм, величине 2 и 3 цм, а акутни кут између њих је 60º. Мања дијагонала паралелепипеда једнака је већој дијагонали базе.
Одлука. Да бисмо сазнали обим паралелепипеда, користимо формулу са основном површином и висином. Обе количине су непознате, али их није тешко израчунати. Прва је висина.
Пошто се мања дијагонала паралелепипеда поклапа сизе витх веће основе, могу се означити једним словом д. Већи угао паралелограма је 120º, јер са 180º чини оштар. Нека друга дијагонала базе буде означена словом “к”. Сада се за двије основне дијагонале могу писати косинуске теореме :
д 2 = а 2 + у 2 - 2ав цос 120º,
к 2 = а 2 + у 2 - 2ав цос 60º.
Проналажење вредности без квадрата нема смисла, јер ће тада поново бити подигнуте на другу снагу. Након добијања супституције података:
д 2 = 2 2 + 3 2 - 2 * 2 * 3 цос 120º = 4 + 9 + 12 * ½ = 19,
к 2 = а 2 + у 2 - 2ав цос 60º = 4 + 9 - 12 * ½ = 7.
Сада ће висина, која је бочна ивица паралелепипеда, бити нога у троуглу. Хипотенуза ће бити позната дијагонала тела, а друга ће бити „к“. Можете написати Питагорову теорему:
н 2 = д 2 - к 2 = 19 - 7 = 12.
Одавде: н = =12 = 2√3 (цм).
Друга непозната количина је подручје базе. Може се рачунати помоћу формуле наведене у другом проблему.
С о = 2 * 3 син 60º = 6 * /3 / 2 = 3√3 (цм2).
Комбинујући све у формули волумена, добијамо:
В = 3√3 * 2√3 = 18 (цм3).
Одговор: В = 18 цм 3 .

Четврти задатак
Цондитион Потребно је знати волумен паралелопипеда који испуњава ове услове: база - квадрат са страном од 5 цм; бочне стране су ромб; један од врхова изнад базе једнако је удаљен од свих врхова у бази.
Одлука. Прво морате да се носите са тим стањем. Са првим параграфом о квадрату нема питања. Други, о ромбовима, јасно показује да је паралелепипед нагнут. Штавише, сви његови рубови су 5 цм, јер су стране ромба исте. И из трећег постаје јасно да су три дијагонале извучене из њега једнаке. Ово су две које леже на бочним странама, а друго је унутар паралелопипеда. И ове дијагонале су једнаке ивици, односно имају и дужину од 5 цм.
Да би се одредила запремина, потребна је формула написана за коси паралелопипед. Опет, не постоје познате вредности. Међутим, површина базе је лако израчунати јер је квадратна.
С о = 5 2 = 25 (цм2).
Мало теже је случај са висином. Биће то у три црте: паралелопипед, четверокутна пирамида и једнакокрачан троугао. Последња околност и потребно је искористити.
Пошто је висина, то је нога у правом троуглу. Хипотенуза у њој ће бити позната ивица, а друга нога је једнака половини дијагонале квадрата (висина је такође медијана). И дијагонала базе је лако пронаћи:
д = √ (2 * 5 2 ) = 5√2 (цм).
Потребно је бројати висину као разлику другог степена ивице и квадрата половине дијагонале и запамтити да је касније извадите. скуаре роот :
н = √ (5 2 - (5/2 * ) 2 ) 2 ) = √ (25 - 25/2) = √ (25/2) = 2,5 (2 (цм).
Остаје да се преброји гласноћа:
В = 25 * 2,5 =2 = 62,5 (2 (цм3).
Одговор: 62.5 (2 (цм3).