Поинцареова претпоставка: историја проблема, доказ, значење

У школи сви познају концепте теореме и хипотезе. По правилу, најједноставнији и нај примитивнији закони утичу на живот, док математичари праве веома сложене претпоставке и постављају занимљиве проблеме. Не увијек, они сами успијевају пронаћи рјешења и доказе, ау неким случајевима и њихови сљедбеници и праведне колеге се већ годинама боре.

Институт Цлаи је 2000. саставио листу од 7 такозваних Миленијумских изазова по аналогији са листом хипотеза из 1900. године. Готово сви ови задаци су сада ријешени, само је један од њих мигрирао на ажурирану верзију. Сада је листа проблема следећа:

• Ходге цоњецтуре;
• једнакост класа П и НП;
• Поинцаре цоњецтуре;
• Ианг-Миллсова теорија;
• Риеманнова хипотеза;
• постојање и глаткоћа решавања Навиер-Стокесових једначина;
• Бирцх-Свиннертон-Диер-ова претпоставка.

Сви они припадају различитим дисциплинама унутар математике и важни су. На пример, Навиер-Стокес-ове једначине се односе на хидродинамику, али у пракси оне могу описати понашање супстанце у земаљској магми или бити корисне у предвиђању времена. Али сви ти проблеми и даље траже свој доказ или порицање. Осим једног.

Поинцареова теорема

Тешко је једноставним ријечима објаснити у чему је проблем, али можете покушати. Замислите сферу, на пример, балон. Све тачке на његовој површини су једнако удаљене од његовог центра, које му не припадају. Али ово је дводимензионално тело, а хипотеза говори о тродимензионалном. Већ је немогуће замислити, али имамо теоријску математику. У овом случају, наравно, све тачке овог тела ће такође бити уклоњене из центра.

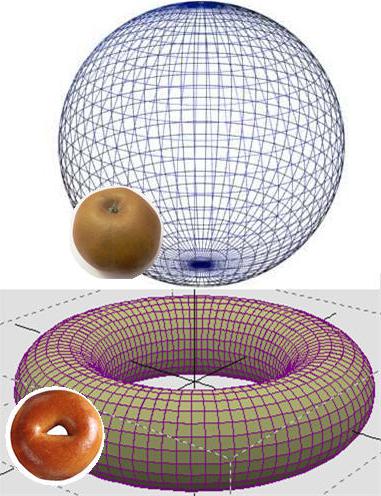
Овај проблем се односи на топологију - науку о својствима геометријских облика. Један од основних појмова у њему је хомеоморфизам, односно висок степен сличности. На пример, можете замислити лопту и торус. Једна фигура се не може добити од друге, избегавајући руптуре, али се конус, коцка или цилиндар из прве могу добити прилично лако. Ово је Поинцареова хипотеза и посвећена је овим метаморфозама са само једном разликом - говоримо о вишедимензионалном простору и телима.

Хистори оф

Френцх матхематициан Хенри Поинцаре студирао је различите области науке. О његовим достигнућима може се рећи, на примјер, чињеница да је он независно од Алберта Ајнштајна изнио главне одредбе посебна теорија релативности. Године 1904. покренуо је проблем да докаже да је свако тродимензионално тело, које поседује одређена својства кугле, управо до деформације. Касније је проширена и генерализована и постала је посебан случај Тхурстонове хипотезе формулисане 1982. године.

Текст

Поинцаре је у почетку оставио такву тврдњу: свако једноставно повезано компактно тродимензионално мноштво без границе је хомеоморфно тродимензионалној сфери. Касније је проширена и генерализована. Ипак, дуго времена је то био изворни задатак који је изазвао највише проблема, а ријешен је само 100 година након његовог појављивања.

Тумачење и значење

То је хомеоморфизам, о чему смо већ говорили. Сада је вредно говорити о компактности и сингуларности. Прво значи да сорта има ограничене величине, не може се непрекидно и бесконачно растезати.

Што се тиче јединствености, можете покушати дати једноставан примјер. Дводимензионална сфера - јабука - има једну занимљиву особину. Ако узмете уобичајену затворену гуму и причврстите је на површину, онда се глатка деформација може смањити на једну тачку. Ово је својство јединствености, али да га представимо у односу на тродимензионални простор прилично тешко.

Једноставно речено, проблематично је било доказати да је сингуларност јединствена својства за сферу. И ако, релативно говорећи, искуство са гуменом траком заврши са таквим резултатом, онда му је тело хомеоморфно. Што се тиче примене ове теорије у животу, Поинцаре је веровао да је Универзум у одређеном смислу тродимензионална сфера.

Прооф оф

Немојте мислити да од десетака математичара који су радили широм света, нико није напредовао ни једну јоту, решавајући овај проблем. Напротив, дошло је до напретка и на крају је довело до резултата. Поинцаре није имао времена да заврши посао, али његово истраживање је озбиљно проширило читаву топологију.

Током 1930-их, интерес за хипотезу се вратио. Пре свега, формулација је проширена на "н-димензионални простор", а онда је амерички Вајтхед пријавио успешне доказе, а касније их је напустио. У 60-70-им годинама, два математичара одједном - Смале и Сталлингс - готово истовремено, али на различите начине развијају рјешење за све н веће од 4.

Године 1982, и за 4, пронађени су докази, преостале су само 3. У истој години, Тхурстон је формулисао хипотезу о геометризацији, а Поинцареова теорија је постала њен посебан случај.

Тада је рад донекле застао - Американац Рицхард Хамилтон је предложио да се Рицци користи у решењу, али је наишао на потешкоће и није довршио истраживање.

За 20 година, Поинцаре хипотеза је као да је заборављена. Руски математичар Григориј Перелман је 2002. године представио решење у општим цртама, шест месеци касније доносећи неке допуне. Касније, ови докази су тестирани и доведени на "сјај" америчких и кинеских научника. И сам Перелман као да је изгубио сваки интерес за проблем, мада је решио општији проблем геометризације, за који је Поинцареова претпоставка само посебан случај.

Признавање и вредновање

Наравно, то је одмах постало сензација, јер се решење једног од Миленијумских проблема једноставно није могло занемарити. Још више изненађује чињеница да је Грегори Перелман одбио све награде и награде, рекавши да већ има диван живот. У умовима обичних људи одмах је постао пример тог полу-лудог генија који је заинтересован само за науку.

Све ово је изазвало доста дискусија у штампи и медијима, да је популарност математичара постала његова. У љето 2014. године, постојале су информације да је Перелман отишао на посао у Шведску, али се испоставило да је то само гласина, он још увијек живи скромно у Ст. Петерсбургу и једва комуницира са било ким. Међу наградама које су му додељене биле су не само Награда Института Цлаи, него и престижна Фиелдс медаља, али он је одбио све. Међутим, Хамилтон, који је, према Перелмановим проценама, дао мање важан допринос доказу, такође није заборављен. У 2009. и 2011. години освојио је и престижне награде и награде.

Цултурал рефлецтион

Упркос чињеници да за обичне грађане и изјава и решење овог проблема немају много смисла, докази су постали познати прилично брзо. Јапански редитељ Масахито Касуга је 2008. године снимио документарац "Документарац" Очаравање Поинцаре Хипотезе ", посвећен својим 100-годишњим покушајима да ријеши овај проблем.

Многи математичари који су били укључени у овај проблем учествовали су у пуцњави, али главни лик, Григориј Перелман, то није желио. Више или мање његових блиских пријатеља такође су учествовали у пуцњави. Документарни филм, који се појавио на екранима након јавног одјека о одбијању научника да прихвати награду, освојио је славу у одређеним круговима и добио неколико награда. Што се тиче масовна култура, Обични људи се још увек питају које аргументе је водио петербуршки математичар, одбијајући да узме новац када га може дати, на пример, у добротворне сврхе.