Ротациони покрет тела. Закон ротационог кретања
Овај чланак описује важан део физике - "Кинематика и динамика ротационог кретања".
Основни појмови кинематике ротационог кретања
Ротациона кретања материјална тачка око фиксне осе назива се такав покрет, чија је путања кружница која се налази у равни окомитој на осу, а њен центар лежи на оси ротације.
Ротационо кретање чврстог тела је кретање у којем се све тачке тела крећу дуж концентричних кругова (чији центри леже на истој оси) у складу са правилом ротационог кретања материјалне тачке.
Нека произвољно круто тијело Т ротира око О оси, која је окомита на равнину слике. На том телу одаберите тачку М. Током ротације ова тачка ће описати кружницу са радијусом р око О осе.
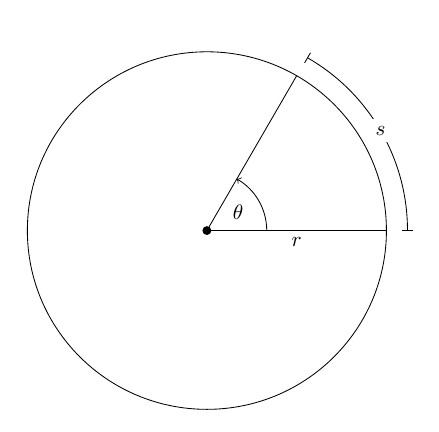
После извесног времена, радијус ће ротирати у односу на почетни положај за угао Δφ.
Смјер десног вијка (у смјеру казаљке на сату) узима се као позитиван смјер вртње. Промена угла ротације са временом се назива једначина ротационог кретања чврстог материјала:
φ = φ (т).
Ако се φ мери у радијанима (1 рад је угао који одговара луку дужине једнаке његовом радијусу), онда је дужина лука кружнице ΔС, коју ће материјална тачка М проћи у времену Δт, једнака:
ΔС = .φр.
Основни елементи кинематике униформног ротационог кретања
Мера кретања материјалне тачке у кратком временском периоду дт је елементарни ротациони вектор дφ .
Угаона брзина Материјална тачка или тело је физичка величина, која се одређује односом вектора елементарне ротације и трајања ове ротације. Правац вектора се може одредити правилом десног вијка дуж осе О. У скаларном облику:
ω = дφ / дт.
Ако је ω = дφ / дт = цонст, онда се такав покрет назива равномерним ротационим кретањем. Када је то угаона брзина се одређује по формули
ω = φ / т.
Према прелиминарној формули, димензија кутне брзине
[ω] = 1 рад / с.
Равномерно ротационо кретање тела може се описати периодом ротације. Период ротације Т је физичка величина која одређује време које је потребно да тело око осе ротације изведе једну потпуну револуцију ([Т] = 1 с). Ако у формули за угаону брзину узмемо т = Т, 2 = 2 π (пуни један заокрет радијуса р), онда
ω = 2π / Т,
стога се период ротације дефинише на следећи начин:
Т = 2π / ω.
Број обртаја које тело направи по јединици времена назива се фреквенција ротације ν, која је једнака:
ν = 1 / Т.
Фреквентне јединице: [ν] = 1 / ц = 1 с -1 = 1 Хз.
Поредећи формуле за брзину кретања и брзину ротације, добијамо израз који се односи на ове величине:
ω = 2πν.
Главни елементи кинематике неравномерног ротационог кретања
Неједнако ротационо кретање чврсте или материјалне тачке око фиксне осе карактерише њена угаона брзина, која се мења са временом.
Вектор ε , који карактерише брзину промене угаоне брзине, назива се вектор кутног убрзања:
ε = дω / дт.
Ако се тело окреће, убрзавајући, дакле дω / дт> 0 , вектор има правац дуж осе у истом правцу као ω.
Ако је ротациони покрет спор - дω / дт <0 , онда су вектори ε и ω супротно усмерени.
Ремарк Када дође до неуједначеног ротационог кретања, вектор ω може да се мења не само по величини, већ иу правцу (када се ротира оса ротације).
Однос величина које карактеришу транслационо и ротационо кретање
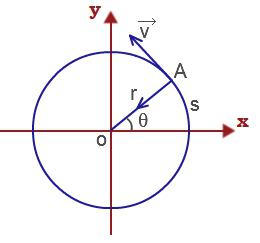
Познато је да је дужина лука са углом ротације радијуса и његова вредност повезана са
ΔС = Δφ р.
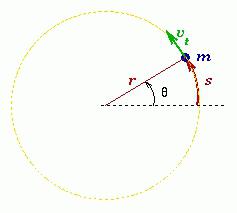
Тада се врши линеарна брзина материјалне тачке која врши ротационо кретање
υ = ΔС / Δт = Δφр / Δт = ωр.
Нормално убрзање материјалне тачке која се обавља ротационо кретање напред дефинишемо на следећи начин:
а = υ 2 / р = ω 2 р 2 / р.
Дакле, у скаларној форми
а = ω 2 р.
Тангенцијална убрзана материјална тачка која врши ротационо кретање
а = ε р.
Тренутак момента материјалне тачке
Векторски производ радијус-вектора путање материјалне тачке масе м и његовим моментом назива се угаони момент ове тачке у односу на ос ротације. Правац вектора може се одредити помоћу правила десног вијка.
Тренутак момента материјалне тачке ( Л и ) усмерен је окомито на равнину нацртану кроз р и и υ и формира десна три вектора са њима (то јест, када се креће од краја вектора р и до у и, десни вијак ће показати правац вектора Л и ).
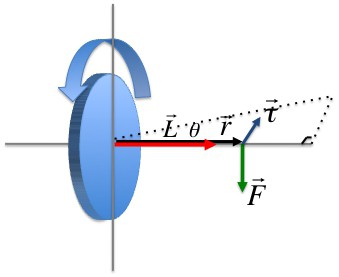
У скаларном облику
Л = м и υ и р и син (υ и , р и ).
Имајући у виду да се при кретању у круг, вектор полупречника и вектор линеарних брзина за и-ту тачку материјала међусобно перпендикуларни,
син (υ и , р и ) = 1.
Дакле, кутни момент материјалне тачке за ротационо кретање ће попримити облик
Л = м и υ и р и .
Тренутак силе који делује на и-тој материјалној тачки
Векторски производ радијуса-вектора, који се држи на месту примене силе, овом силом се назива моментом силе која делује на и-ту тацку материјала у односу на ос ротације.
У скаларном облику
М и = р и Ф и син (р и , Ф и ).
Под претпоставком да је р и синα = л и , Ми и = л и Ф и .
Вредност л и једнака дужини окомице која се спушта од тачке ротације ка смеру силе, назива се раме силе Ф и .
Ротациона динамика
Једнаџба динамике ротационог кретања је записана као:
М = дЛ / дт.
Текст закона је следећи: брзина промене угаоног момента тела, која се ротира око фиксне осе, једнака је резултујућем моменту око ове осе свих спољашњих сила примењених на тело.
Тренутак импулса и момент инерције
Познато је да је за и-ту материјалну тачку кутни момент у скаларном облику дат формулом
Л и = м и υ и р и .
Ако уместо линеарне брзине замени своју експресију преко угла:
υ и = ωр и ,
тада израз за кутни момент добија облик
Л и = м и р и 2 ω.
Количина И и = м и р и 2 се назива моментом инерције око осе и-те материјалне тачке апсолутно крутог тела које пролази кроз његов центар масе. Онда угаони момент материјалне тачке коју пишемо:
Л и = И и ω.
Тренутак импулса апсолутно крутог тела пише се као сума импулсних момента материјалних тачака које чине ово тело:
Л = Иω.
Тренутак силе и момент инерције
Закон ротационог кретања гласи:
М = дЛ / дт.
Познато је да представља тренутак боди импулсе могуће кроз тренутак инерције:
Л = Иω.
Онда
М = Идω / дт.
С обзиром да је кутно убрзање одређено изразом
ε = дω / дт,
добијамо формулу за тренутак силе који представља момент инерције:
М = Иε.
Ремарк Тренутак силе сматра се позитивним ако је кутно убрзање којим је проузроковано веће од нуле, и обрнуто.
Стеинер теорема. Закон додавања момената инерције
Ако оса ротације тела пролази центар масе не пролази, онда у односу на ову осу можете наћи њен моменат инерције према Стеинер-овој теореми:
И = И 0 + ма 2 ,
где је И 0 - почетни момент инерције тела; м је маса тела; а је удаљеност између оса.
Ако се систем, који се врти око фиксне осе, састоји од н тела, тада ће укупни моменат инерције овог типа система бити једнак збиру тренутака који га чине (закон додавања момената инерције).