Неке тачке о томе како се рјешава неједнакост
Једна од тема која захтијева максималну пажњу и истрајност од ученика је рјешавање неједнакости. Овако сличне једначине и истовремено се веома разликују од њих. Зато што њихово решење захтева посебан приступ.
Својства која ће бити потребна за проналажење одговора
Све се користе за замјену постојећег записа еквивалентним. Већина њих је слична оној у једнаџбама. Али постоје разлике.
- Функција која је дефинисана у ЛДУ, или било који број може се додати на обе стране оригиналне неједнакости.
- Слично томе, мултипликација је могућа, али само позитивном функцијом или бројем.
- Ако се ова радња изводи са негативном функцијом или бројем, онда се знак неједнакости мора замијенити супротним.
- Функције које нису негативне могу се подићи на позитивну снагу.
Понекад је решавање неједнакости праћено акцијама које дају вањске одговоре. Потребно их је елиминисати упоређивањем домена ДХС и разних решења.
Користећи метод размака
Његова суштина је да редукује неједнакост на једначину, у којој је на десној страни нула.
- Одредите област где се налазе валидне вредности варијабли, тј. ЛДЛ.
- Преобразите неједнакост уз помоћ математичких операција тако да у десном делу има нулу.
- Замените знак неједнакости са "=" и решите одговарајућу једначину.
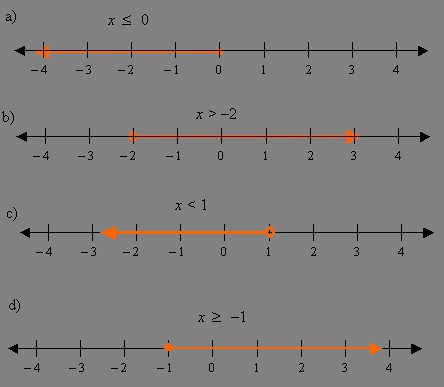
- На нумеричкој оси означите све одговоре који су се појавили током решења, као и ТЛД интервале. Са строгом неједнакошћу тачке коју треба да нацртате. Ако постоји знак једнакости, онда они треба да насликају.
- Одредите знак оригиналне функције на сваком интервалу који произлази из тачака ЛДД-а и поделите његове одговоре. Ако се при преласку кроз тачку знак функције не промијени, онда улази у одговор. Иначе - искључена.
- Граничне тачке за ТЛД треба додатно проверити и тек онда укључити или не у одговор.
- Одговор, који се добија, мора бити написан у облику уједињених скупова.
Мало о двоструким неједнакостима
Они користе два знака неједнакости у записнику. То значи да је нека функција ограничена условима одмах два пута. Такве неједнакости се решавају, као систем од два, када је оригинал подељен на делове. И у интервентној методи приказани су одговори из решења обеју једначина.
Да би их се решило, такође је дозвољено да се користе горе наведена својства. Уз њихову помоћ, погодно је да се неједнакост сведе на једнакост нула.

Каква је ситуација са неједнакостима у којима постоји модул?
У овом случају, решење неједнакости користи следеће особине, и оне су тачне за позитивну вредност "а".
Ако "к" узима алгебарски израз, онда су такве замене тачне:
- | к | <а до -а <к <а;
- | к | > а на к <-а или к> а.
Ако неједнакости нису стриктне, онда су и формуле тачне, само у њима, осим знака више или мање, појављује се "=".
Како ријешити систем неједнакости?
Ово знање ће бити потребно у случајевима када је такав задатак дат или постоји евиденција двоструке неједнакости или се модул појављује у запису. У таквој ситуацији, решење би биле вредности варијабли које би задовољиле све неједнакости у запису. Ако таквих бројева нема, систем нема рјешења.
План решења система неједнакости:
- ријешити сваку од њих посебно;
- нацртати све интервале на нумеричкој оси и одредити њихове пресеке;
- напишите одговор система, који ће бити спој онога што се десило у другом параграфу.
Како се носити са фракцијским неједнакостима?
Пошто је током њиховог решавања можда потребно да се промени знак неједнакости, потребно је пажљиво и пажљиво извршити све тачке плана. У супротном, може бити супротан одговор.
Рјешење фракцијских неједнакости такођер користи интервалну методу. А акциони план ће бити:
- Користећи описана својства, дајте фракцији такав изглед да остаје само нула десно од знака.
- Замените неједнакост са "=" и одредите тачке у којима ће функција бити једнака нули.
- Означите их на координатној оси. У овом случају, бројеви који су резултат калкулација у имениоцу ће увек бити пробушени. Сви остали - на основу услова неједнакости.
- Одредите интервале конзистентности.
- У одговору, напишите унију тих интервала, чији знак одговара ономе што је било у првобитној неједнакости.
Ситуације у којима се ирационалност појављује у неједнакости
Другим речима, постоји математички корен у запису. Пошто се у школском току алгебре највише бави задацима скуаре роот онда ће то бити размотрено.
Решење ирационалних неједнакости је да се добије систем од два или три, који ће бити еквивалент оригиналу.
| Оригинал неједнакост | стање | еквивалентни систем |
| (Н (к) <м (к) | м (к) је мањи или једнак 0 | но солутионс |
| м (к) већи од 0 | н (к) је већи или једнак 0 н (к) <(м (к)) 2 | |
| (Н (к)> м (к) | м (к) је већи или једнак 0 н (к)> (м (к)) 2 | |
или н (к) је већи или једнак 0 м (к) је мањи од 0 | ||
| (Н (к) ≤ м (к) | м (к) је мањи од 0 | но солутионс |
| м (к) је већи или једнак 0 | н (к) је већи или једнак 0 н (к) ≤ (м (к)) 2 | |
| (Н (к) ≥ м (к) | м (к) је већи или једнак 0 н (к) ≥ (м (к)) 2 | |
или н (к) је већи или једнак 0 м (к) је мањи од 0 | ||
| (Н (к) <(м (к) | н (к) је већи или једнак 0 н (к) је мања од м (к) | |
| (Н (к) * м (к) <0 | н (к) је већи од 0 м (к) је мањи од 0 | |
| (Н (к) * м (к)> 0 | н (к) је већи од 0 м (к) већи од 0 | |
| (Н (к) * м (к) ≤ 0 | н (к) је већи од 0 м (к) ≤0 | |
или н (к) је 0 м (к) - било који | ||
| (Н (к) * м (к) ≥ 0 | н (к) је већи од 0 м (к) ≥0 | |
или н (к) је 0 м (к) - било који |
Примери решавања различитих типова неједнакости
Да би се додала јасноћа у теорију решавања неједнакости, доле су примери.
Први примјер. 2к - 4> 1 + к
Решење: да би се одредио ТЛД, довољно је само пажљиво погледати неједнакост. Формира се из линеарних функција, па је дефинисана за све вредности променљиве.
Сада са обе стране неједнакости треба одузети (1 + к). Испоставља се: 2к - 4 - (1 + к)> 0. Након што су заграде отворене и дати такви термини, неједнакост поприма следећи облик: к - 5> 0.
Изједначавајући га са нулом, лако је пронаћи његово решење: к = 5.
Сада ову тачку са бројем 5, морате означити на координатном снопу. Затим проверите знакове оригиналне функције. У првом интервалу од минус бесконачности до 5, можете узети број 0 и заменити га неједнакост која је резултат трансформација. Након калкулација, испало је -7> 0. испод лука интервала морате потписати знак минус.
У следећем интервалу од 5 до бесконачности, можете изабрати број 6. Онда се испостави да је 1> 0. Под луком, знак “+” је потписан. Овај други интервал ће бити одговор на неједнакост.
Одговор: к лежи у интервалу (5; ∞).
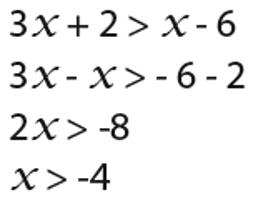
Други пример. Потребно је ријешити сустав од двије једнаџбе: 3к + 3 ≤ 2к + 1 и 3к - 2 ≤ 4к + 2.
Одлука. ЛДЛ ових неједнакости такође лежи у домену било ког броја, пошто су дате линеарне функције.
Онда морате да делујете у фазама. Прво претворите прву од неједнакости и изједначите је са нулом. 3к + 3 - 2к - 1 = 0. То је, к + 2 = 0. Дакле, к је -2.
Друга неједнакост ће имати облик такве једнаџбе: 3к - 2 - 4к - 2 = 0. Након трансформације: -к - 4 = 0. Она даје вредност за променљиву која је једнака -4.
Ова два броја треба да буду означена на оси, приказујући интервале. Пошто неједнакост није стриктна, све тачке морају бити обојене. Први интервал од минус бесконачности до -4. Нека број буде -5. Прва неједнакост ће дати вредност -3, а друга 1. Дакле, ова празнина не улази у одговор.
Други интервал је од -4 до -2. Можете одабрати број -3 и замијенити га у обје неједнакости. У првом и другом се добија вредност -1. Дакле, под луком "-".
У последњем интервалу од -2 до бесконачности, најбољи број је нула. Потребно га је заменити и пронаћи вредности неједнакости. У првом се добија позитиван број, а други је нула. Овај недостатак би такође требало да буде искључен из одговора.
Од три интервала, решење неједнакости је само једно.
Одговор: к припада [-4; -2].

Трећи пример. | 1 - к | > 2 | к - 1 |
Одлука. Први корак је одређивање тачака на којима функције нестају. За лијево овај број ће бити 2, за десну - 1. треба их означити на зраку и одредити интервале сталности знака.
У првом интервалу, од минус бесконачности до 1, функција са леве стране неједнакости има позитивне вредности, а са десне стране негативне вредности. Под луком, треба да запишете два знака "+" и "-" један поред другог.
Следећи интервал је од 1 до 2. На њему обе функције узимају позитивне вредности. Дакле, под луком, два плус.
Трећи интервал од 2 до бесконачности даје следећи резултат: лева функција је негативна, десна позитивна.
Узимајући у обзир добијене знакове, потребно је израчунати вриједности неједнакости за све интервале.
Прво, добијамо следећу неједнакост: 2 - к> - 2 (к - 1). Минус пре два у другој неједнакости је последица чињенице да је ова функција негативна.
Након трансформације, неједнакост изгледа овако: к> 0. Она одмах даје вредности варијабле. То значи да ће се из овог интервала вратити само интервал од 0 до 1.
На другом: 2 - к> 2 (к - 1). Конверзије ће дати следећу неједнакост: -3к + 4 више од нуле. Његова нула је к = 4/3. Узимајући у обзир знак неједнакости, испада да к мора бити мањи од тог броја. Дакле, овај интервал се своди на интервал од 1 до 4/3.
Ово последње даје следећи запис о неједнакости: - (2 - к)> 2 (к - 1). Његова трансформација доводи до следећег: к> 0. То значи да је једначина тачна за к мања од нуле. То значи да у траженој празнини неједнакост не даје рјешења.
У прва два интервала, граница се показала као број 1. Потребно је да се провери одвојено. То значи, замијенити изворну неједнакост. Испада: | 2 - 1 | > 2 | 1 - 1 | Израчун даје да је 1 већи од 0. Ово је валидна изјава, тако да је један укључен у одговор.
Одговор: к лежи у интервалу (0; 4/3).