Шта је конус? Концепт и фотографија
Стереометрија је важан део геометрије, чији су предмет истраживања особине и карактеристике фигура у тродимензионалном простору. У овом чланку ћемо размотрити једну од таквих волуметријских цифара. Хајде да се упознамо са питањем шта је конус.
Цоне фигуре
Дајемо најопћенитију дефиницију конуса. Под овом сликом разумемо површину која се формира као резултат повезивања правих сегмената одређене тачке у простору са свим тачкама дате криве. У овом случају, одређена тачка у простору не би требало да буде у равни криве. На пример, ако крива има облик параболе, онда ће се цифра добијена описаним методом назвати параболични конус, ако је крива елипса, конус ће бити елиптичан, и тако даље.
Ad
После давања геометријске дефиниције шта је конус, представљамо фотографију која приказује визуелно могуће облике ове фигуре.

Гледајући ову фотографију, многи су у њој видјели облик дјечје шешире, коју је носио Буратино, чашу за вафл од сладоледа у облику рога или упозорење наранчасти и црни пругасти пут.

Стожац геометријских елемената
Да би боље разумели питање шта је конус, треба навести геометријска имена елемената ове просторне фигуре.
Конус је омеђен са две површине. Први се зове база. То је равнина која је ограничена горе наведеном кривуљом. На пример, то може бити круг или елипса. Друга површина је страна облика и назива се конична. Не лежи у истој равни, већ се може претворити у равну слику, као што ће бити објашњено у наставку.
Ad
Један од важних елемената конуса је његов врх. Ова тачка ограничава конусну површину. На њега су повезане све тачке основне кривуље.
Сегмент који повезује врх базе, назива се генератрик, или формира конус. Заузврат, кривуља која граничи са базом названа је директном линијом, или водичем.
Подручја коничне површине и базе чине укупну површину конуса. Запремина простора коју ова два подручја ограничавају је запремина конуса.
Округли равни конус и његове линеарне карактеристике
Изнад је дата општа дефиниција шта је конус. Ипак, често у пракси иу геометријским проблемима постоји специфичан облик ове фигуре - раван кружни конус. То је приказано испод.
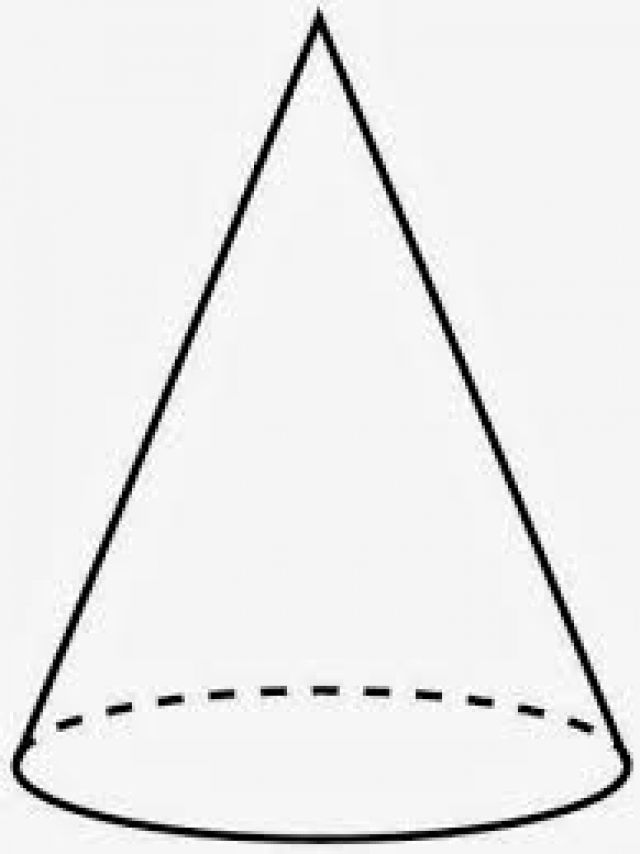
Основа ове фигуре је круг. То се назива правим јер окомица која је пала на своју основу са висине ће сећи у круг у његовом тачном центру. Ако овај услов није задовољен, онда можемо говорити о нагнутом конусу.
Линија која повезује врх са средиштем круга назива се оса слике. То је и ос ротације конуса. Заиста, ако узмете прави троугао и почнете га ротирати око једне од ногу, тада ће резултат бити раван конус са округлом базом. Овај метод добијања конуса је схематски приказан испод.
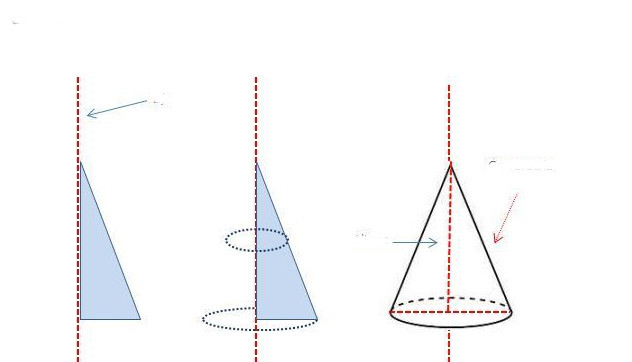
Може се видети да ће генератор бити једнак дужини хипотенузе троугла. Нога, око које је извршена ротација, постаће висина тродимензионалне фигуре, а друга нога ће бити једнака радијусу конуса (радијус кружне базе).
Једна од важних карактеристика дотичне фигуре је да су дужине свих генератора за њу једнаке једна другој. Ова чињеница нам омогућава, користећи Питагорину теорему, да напишемо математичку везу између три главна линеарна параметра облика:
Ad
г 2 = р 2 + х 2
Квадрат генератора правог кружног конуса је једнак збиру квадрата његовог радијуса р и висине х.
Испитујући питање шта је конус равна линија са кружном базом, покажимо како је њена површина и волумен могући.
Одређивање површине
Као што је већ напоменуто, површина фигуре је обликована коничном површином и равном базом. Која је њихова област? Са самопоуздањем можете одговорити на ово питање ако погледате раван скен кружног конуса. Резањем базе са бочне површине, и резањем потоње уздуж генератора, добијамо следећи резултат.
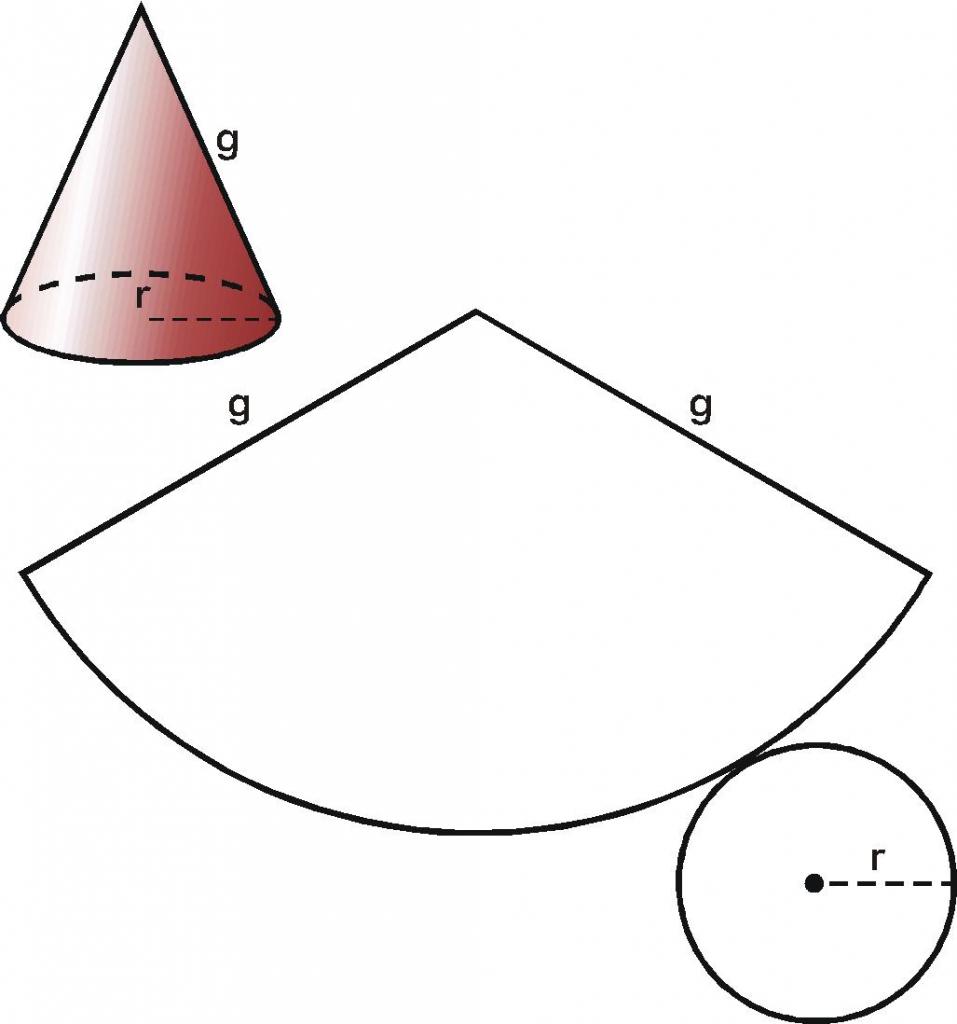
Нема проблема са одређивањем површине круга. Формула за њено подручје је позната сваком студенту. Запишите:
С о = пи * р 2
Симбол С о је подручје базе слике.
Бочна површина конуса на равном скенирању представљена је кружним сектором, чији је полупречник једнак дужини генератора, а дужина лука на којој се сектор налази једнака је дужини обима базе. Ови подаци нам омогућују да једнозначно одредимо подручје сектора. Нећемо давати интервентне прорачуне за добијање формуле за квадрат С б бочне површине конуса. Пишемо коначни резултат:
Ad
С б = пи * г * р
Пошто је генерица г увек већа од радијуса р, површина бочне површине фигуре ће, за било које параметре, бити већа од површине базе.
Формула за укупну површину има облик:
С = С о + С б = пи * р * (р + г)
Одређивање обима слике
Читаоци су можда приметили да облик конуса подсећа на неку пирамиду, само је њена бочна површина глатка и не ребраста, као пирамида. Ова аналогија има геометријско оправдање, пошто се повећање броја бочних страна пирамиде у бесконачност преводи у конус. Ова чињеница дозвољава да се за запремину стошца запише тачно иста формула као и за волумен пирамиде. Имамо:
В = 1/3 * х * С о
Треба имати у виду да није битно која је затворена крива основа конуса, такође није битно да ли је фигура равна или коса, формула ће бити валидна у свим овим случајевима.
За конус круга, израз за В поприма посебан облик:
В = 1/3 * пи * р 2 * х
Задатак одређивања површине конуса кроз његов волумен
Показујемо како да користимо писане формуле.
Претпоставимо да је волумен округлог конуса 50 цм3. Потребно је израчунати његову површину ако је радијус р три пута мањи од висине х.
Пишемо формулу за волумен и однос висине х са радијусом р у складу са условима проблема:
В = 1/3 * пи * р 2 * х;
х = 3 * р.
Из ових једначина добијамо:
В = 1/3 * пи * р 2 * 3 * р =>
р = (В / пи) ≈ 2.516 цм;
х = 3 * ∛ (В / пи) ≈ 7.547 цм.
Добијене вредности нам омогућавају да израчунамо дужину генералног генератора конуса:
г = √ (х 2 + р 2 ) = 7,955 цм.
Формула за површину слике је:
С = пи * р * (р + г)
Утврдили смо све потребне количине (р и г). Замењујући њихове нумеричке вредности у једнакост, добијамо одговор: С = 82,72 цм2.