Који је тренутак инерције: формуле за штап и точак

Свако кретање тела у простору, чија је путања круг, подразумева познавање не само угаоне брзине, већ и момента инерције за опис овог кретања. Који је тренутак инерције, као и оно што је једнако за штап и точак, овај чланак ће одговорити.

Ротација и момент инерције

Физичка величина, која се назива момент инерције, означена је, по правилу, словом И и појављује се у физици када се разматра угаони момент материјалне тачке, која се ротира око осе. Кутни момент Л у скаларној форми пише се следећим изразом:

Л = р * м * в

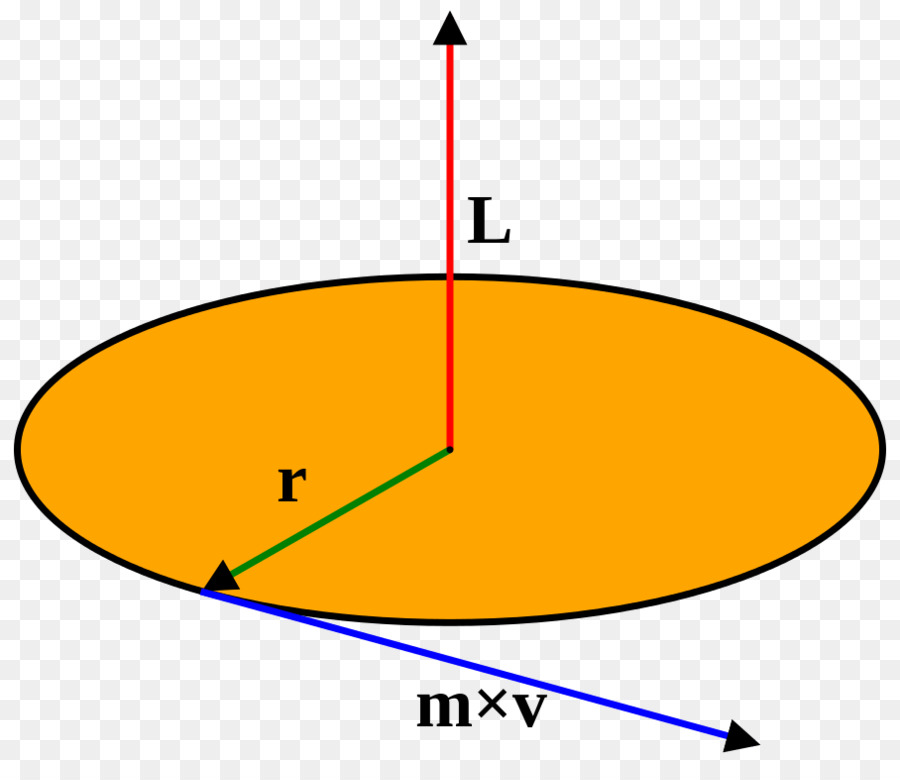
Овде је р удаљеност до оси материјалне тачке, м је њена маса, в је линеарна брзина. Користећи однос последњег са углом брзине ω, добијамо израз:

Л = р ² * м * ω, где ω = в / р

Одговарајући на питање шта је момент инерције, треба рећи да је то вредност И = р ² * м. То јест, зависи од масе ротирајућег објекта, брзо расте са растућим растојањем до осе и мери се у кг * м ² .

Општи израз за момент инерције

Формула која је представљена у претходном параграфу за вредност И је валидна ако су димензије објекта занемариве у односу на удаљеност од р оси (Земља се ротира око наше звезде). Ако линеарне димензије објекта постану упоредиве са удаљеностима р, онда је потребно израчунати И да користимо општу формулу, која је дата у наставку:

И = ( _м (р ² * дм)

То показује да је интегранд момент момента инерције материјалне тачке. Збир свих момената из тачака са масом дм је укупан момент инерције И за цело тело.

Ова формула је моћно средство за одређивање И тијела апсолутно било којег облика. Према формули, вредност И је адитивна, то јест, омогућава вам да поделите тело на одвојене делове, израчунате њихове моменте инерције, а затим додате резултате да бисте добили вредност тела И.

Физичко значење И

Знајући шта је момент инерције, потребно је рећи неколико речи о томе како његова вредност утиче на понашање и карактеристике ротације реалних објеката.

Велика вредност И доводи до чињенице да се тело тешко окреће око осе. Да бисте то урадили, морате обавити значајан посао и уложити значајне напоре. Пример тела са великим И је замашњак за кола - тешки метални диск који је чврсто постављен на радилицу мотора. Напротив, ако је вредност система И мала, онда се она може брзо одмотати и исто тако брзо и лако зауставити. Пример за то је алуминијумски наплатак бициклистичког точка.

Горе наведена дискусија сугерише да је момент инерције окарактерисан инерцијом процеса ротације, тј. Он има исту улогу као и маса тела када се на њу примени сила да би се убрзало.

Разлика између масе и момента инерције лежи не само у мерним јединицама, већ иу чињеници да је ово функција функције ротационог система, а не само геометрија тела и његове масе.

Тренутак инерције око осе ротације која се сијече центар масе шипке

Размотримо пример коришћења интегралне формуле за решавање стварних проблема. Пре свега, решавамо једноставан проблем: постоји танак штап дужине л и масе м. Оса се ротира окомито на овај штап кроз центар масе објекта. Потребно је одредити вредност И за овај систем.

Пишемо општу формулу за инерцију момента штапа око осе, имамо:

И = ( _м (р ² * дм)

Пошто је оса окомита на предметно тело, а сама шипка је бесконачно мале дебљине, могуће ју је ментално пресећи у танке слојеве са равнима паралелним са осом. У овом случају, налазимо да се елемент масе дм може представити следећом једначином:

дм = ρ * с * др

Овде је р густина материјала, С је попречни пресек, који је константан и тежи нули (штап је бесконачно танак). Замените овај израз општој формули:

И = ρ * С * ∫ ^{+ л / 2} _{-л / 2} (р ² * др)

Треба напоменути да замењене интеграционе границе за р одговарају стању проблема (оса дели штап на два једнака дела). Обављајући интеграцију, добијамо:

И = ρ * С * (р 3/3) | ^{+ л / 2} _{-л / 2} = м * л 2/12, где је м = ρ * С * л

Тако је момент инерције танке шипке, када оса пролази кроз центар масе, 12 пута мањи од оног за материјалну тачку исте масе која се налази на удаљености л од осе.

Вредност И за шипку са осом ротације на крају објекта

Размотрите шта је тренутак инерције у нешто другачијој ситуацији. Имамо исти објекат (танки штап), али сада оса пролази кроз крај. Како ће се у овом случају промијенити тренутак инерције? Користећи исту методу раздвајања штапа и накнадну интеграцију, као у претходном параграфу, добијамо:

И = ρ * С * ∫ ^л ₀ (р ² * др)

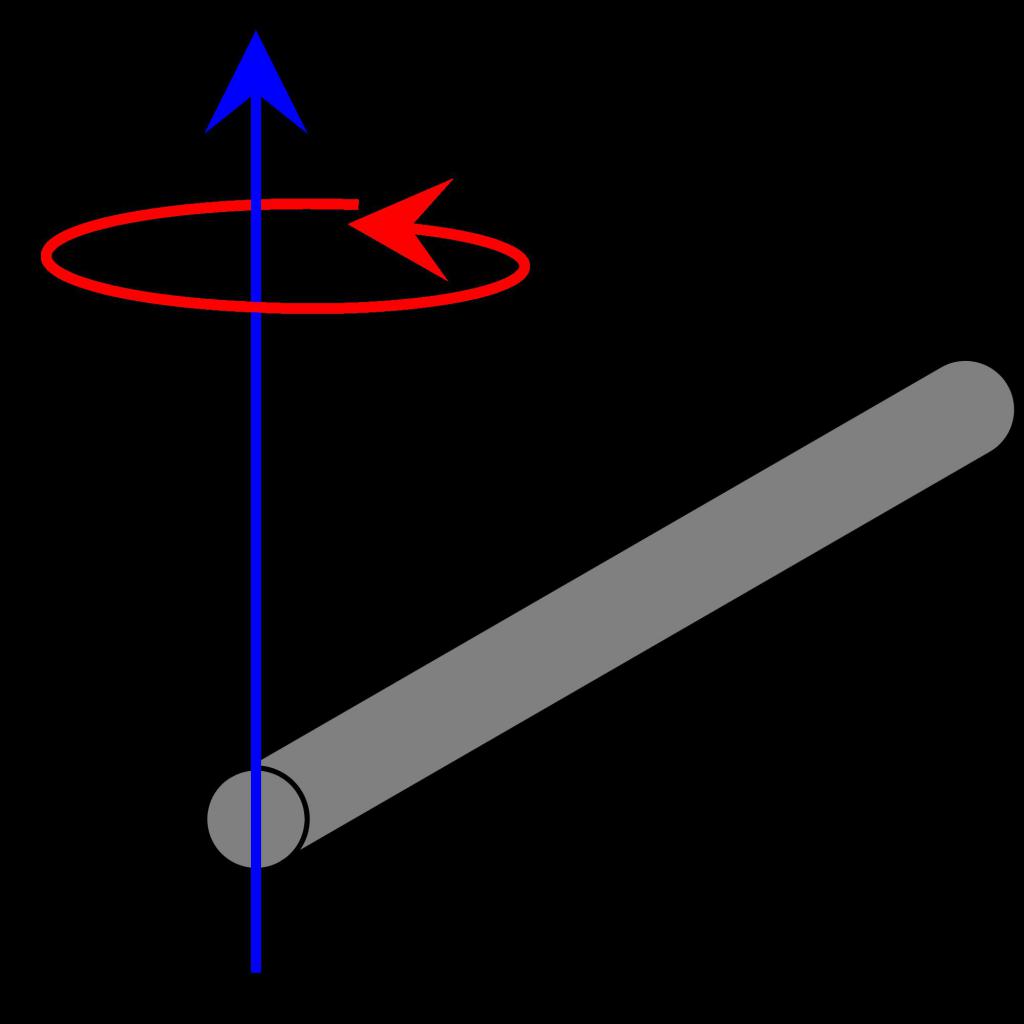
Имајте на уму да су се само границе интеграције промениле. Рјешење је сљедећа једнакост:

И = м * л 2/3

Израз показује да ће исти штап имати 4 пута већи момент инерције (теже се окретати) ако се ос ротације помјери од центра до руба.

Узимајући у обзир решење ова два проблема, важан је закључак: при израчунавању вредности И, немогуће је смањити целу масу објекта до његовог центра и извршити прорачун као за материјалну тачку. Прорачун треба извршити само помоћу интегралног израза.

Вредност за точак

Тренутак инерције точка може се одредити употребом својства адитивности разматране количине. Да бисте то урадили, ментално раставите точак у одвојеним деловима, који представљају жбице и обод. Будући да је игла танак штап, а његова ос ротације пролази кроз крај, тада је формула за њу добивена у претходном параграфу.

Што се тиче наплатка, његов момент инерције сличан је моменту за материјалну тачку која се налази на растојању од радијуса точка и има масу обода.

Додајући моменте инерције свих елемената, добијамо:

И = н * м _ц * р 2/3 + м _о * р ²

Овде су м _ц и м _о жбице и маса обода, респективно, н је број жбица. Ако све жбице теже много мање од обода, онда ће инерција точкова бити једнака:

И = м _о * р ² ако је н * м _ц < о

Познавање вредности И за точак је важно при израчунавању угаоне брзине и угаоног момента ротације точкова било ког возила (аутомобила, бицикла).