Каква је моћ абецеде

Абецеда у рачунарству је знакски систем, којим можете послати информативну поруку. Да бисмо разумели суштину ове дефиниције, ево неколико додатних теоријских чињеница:

1. Свака порука се састоји од абецеде. На пример, овај чланак је порука. Затим се састоји од знакова руске абецеде.
2. Под симболом можемо разумети минималну значајну честицу абецеде. И недељиве честице се називају атоми. Знакови у руском писму су "а", затим "б", "ц", и тако даље.
3. У теорији, абецеда не мора да буде кодирана на било који начин. На пример, у штампаној књизи, симболи алфабета значе сами себе, што значи да немају никакво кодирање.

Али у пракси имамо следеће: рачунар не разуме која су слова. Стога, да би се послала информативна порука, она мора прво бити кодирана на језику разумљивом компјутеру. Да би наставили даље, потребно је увести додатне термине.

Каква је моћ абецеде

Под јачином абецеде подразумевамо укупан број знакова у њему. Да бисте сазнали која је снага абецеде, треба да бројите број знакова у њој. Хајде да схватимо. За руску абецеду, снага абецеде је 33 или 32 знака, ако не користите "е".

Претпоставимо да се сви карактери наше абецеде сусрећу са једнаком вероватноћом. Ова претпоставка се може схватити на следећи начин: претпоставимо да имамо торбу са потписаним коцкама. Број коцки у њему је бесконачан и сваки је потписан са само једним симболом. Затим, уз равномјерну расподјелу, без обзира колико коцки изашли из вреће, број коцки са различитим симболима ће бити исти, или ће тежити томе са повећањем броја коцки које извучемо из торбе.

Процена тежине информативних порука

Пре скоро стотину година, амерички инжењер Ралпх Хартлеи је извео формулу са којом можете да процените количина информација у поруци. Његова формула ради за једнако могуће догађаје и изгледа овако:

и = лог ₂ М

Где је "и" број недељивих информационих атома (битова) у поруци, "М" је снага абецеде. Пратимо. Помоћу математичких трансформација можемо утврдити да се снага абецеде може израчунати на следећи начин:

М = 2 ^и

Ова формула у општој форми поставља везу између броја једнако вероватних догађаја "М" и количине информација "и".

Израчунај снагу

Вероватно већ знате из курса рачунара у школи да се у модерним рачунарским системима који су изграђени на вон Неуманновој архитектури користи бинарни систем кодирања информација. Овако се кодирају и програми и подаци.

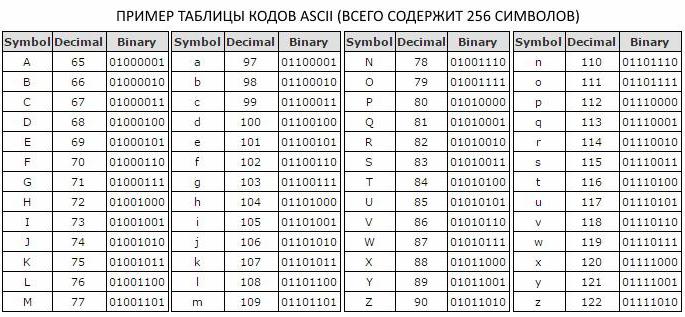
Да бисте приказали текст у рачунарском систему, користите јединствени код од осам битова. Шифра се сматра униформном јер садржи фиксни скуп елемената - 0 и 1. Вриједности у таквом коду су специфициране специфичним редослиједом ових елемената. Уз помоћ осмобитног кода, можемо кодирати поруке тежине 256 бита, јер по Хартлевој формули: М ₈ = 2 ⁸ = 256 бита информација.

Ова ситуација са кодирањем знакова у бинарном коду развила се историјски. Али теоретски бисмо могли користити друге алфабете за представљање података. Тако, на пример, у абецеди од четири слова, сваки знак би имао тежину не једног, већ два бита, у абецеди од осам карактера - 3 бита, и тако даље. Ово се израчунава помоћу бинарног логаритма датог горе ( и = лог ₂ М ).

Пошто се у алфабету са капацитетом од 256 бита, додељује осам бинарних цифара за означавање једног карактера, одлучено је да се уведе додатна мера информација - бајтова. Један бајт садржи један знак АСЦИИ шифре и садржи осам битова.

Како мјерити информације

в прописном и строчном варианте, цифры, символы знаков препинания и другие базовые символы. Осам-битно кодирање текстуалних порука, које се користи у АСЦИИ шифри, омогућава вам да уклопите основни скуп латиничних и ћириличних знакова у велика и мала слова, бројеве, знакове интерпункције и друге основне знакове.

Да бисте измерили веће количине података, користите посебне префиксе за речи бајт и бит. Такви прилози су приказани у табели испод:

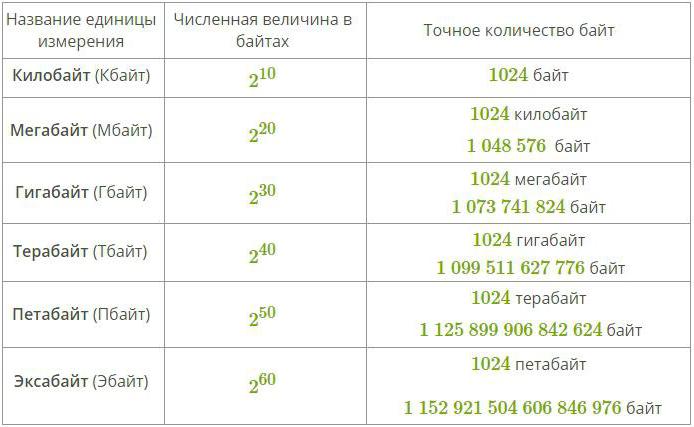
Многи људи који су проучавали физику ће тврдити да би било рационално користити класичне префиксе за означавање јединица информација (као што су кило и мега), али у ствари то није сасвим тачно, јер такви префикси за вредности означавају множење за један или други степен од десет. када се бинарни систем мерења користи свуда у рачунарству.

Исправите имена јединица података

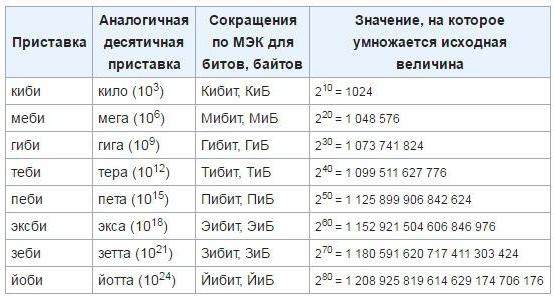
У циљу отклањања нетачности и непогодности, у марту 1999. године, Међународна комисија за електротехнику одобрила је нове јединице јединицама, које се користе за одређивање количине информација у електронској рачунарској технологији. Такви префикси су "меби", "киби", "гиби", "теби", "ексби", "петит". До сада се ове јединице још нису укоријениле, тако да је највјероватније потребно вријеме за увођење овог стандарда и почетак широке употребе. Како направити прелаз са класичних јединица на ново одобрене, можете одредити следећу табелу:

Претпоставимо да имамо текст који садржи К знакова. Затим, користећи абецедни приступ, можете израчунати количину информације В која садржи. Он ће бити једнак производу снаге абецеде према тежини информација једног карактера у њој.

По Хартлијевој формули, знамо како израчунати количину информација кроз бинарни логаритам. Под претпоставком да је број знакова абецеде једнак Н и да је број знакова у запису информативне поруке једнак К, добијамо сљедећу формулу за израчунавање волумена информације поруке:

В = К ₂ лог ₂ Н

Абецедни приступ указује да ће волумен информација зависити само од моћи абецеде и величине порука (то јест, броја знакова у њој), али ни на који начин неће бити повезан са семантичким садржајем за особу.

Примјери израчунавања снаге

У учионици информатика често даје задатак проналажења моћи абецеде, дужине поруке или обима информација. Ево једног од следећих задатака:

"Текстуална датотека заузима 11 КБ простора на диску и садржи 11264 карактера. Одредите снагу абецеде ове текстуалне датотеке."

Шта ће бити решење, можете видети на слици испод.

Тако абецеда са капацитетом од 256 карактера носи само 8 битова информација, што се у информатичкој науци назива један бајт. Бајт описује 1 карактер АСЦИИ табеле, која, ако размислите о томе, уопште није пуно.

Да ли је један бајт много или мало?

Модерна складишта података као што су дата центри Гоогле-а и Фацебоок-а садрже не мање од десетине петабајта информација. Тачна количина података, међутим, биће тешко израчунати чак и сама, јер ћете онда морати да зауставите све процесе на серверима и блиске кориснике приступа снимању и уређивању њихових личних података.

Али, да би се замислиле такве непојмљиве количине података, потребно је јасно схватити да се све састоји од ситних детаља. Потребно је разумети шта је снага абецеде (256) и колико битова садржи 1 бајт информација (као што се сећате, 8).