Аритметичка прогресија - нумеричка секвенца
Неко је опрезан са речју "прогресија" као веома компликован термин из делова више математике. У међувремену, најједноставнија аритметичка прогресија је рад такси шалтера (где и даље остају). А разумевање суштине (иу математици не постоји ништа важније од „разумети суштину“) аритметичке секвенце није тако тешко, схватајући неколико основних појмова.
Математичка секвенца бројева
Бројчани низ се обично назива низом бројева, од којих сваки има свој број.
и 1 - први члан секвенце;
и 2 - други члан секвенце;
...
и 7 - седми члан секвенце;
...
и н је н-ти члан секвенце;
Међутим, не занима нас било који произвољни скуп бројева и бројева. Наша пажња ће бити усмерена на нумеричку секвенцу, у којој је вредност н-тог термина везана за њен редни број односом који се може јасно изразити математички. Другим речима: нумеричка вредност н-тог броја је функција н.
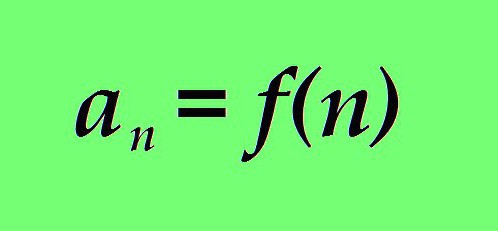
где:
а је вредност члана нумеричке секвенце;
н је његов редни број;
ф (н) је функција, где је редни број у нумеричкој секвенци н аргумент.
Дефиниција
Аритметичка прогресија се назива нумеричка секвенца у којој је сваки наредни термин више (мањи) од претходног по истом броју. Формула за н-ти термин аритметичке секвенце је следећа:
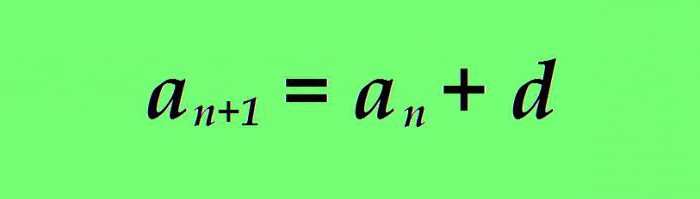
где
а н - вредност тренутног члана аритметичке прогресије;
а н + 1 је формула за следећи број;
д - разлика (одређени број).
Лако је одредити да ако је разлика позитивна (д> 0), онда ће сваки наредни члан серије која се разматра бити већи од претходног и таква аритметичка прогресија ће се повећавати.
Пример:
а 1 = 5
д = 3
онда
број члана - н | 1 | 2 | 3 | 4 | 5 | 6 |
вредност члана - а н | 5 | 8 | 11 | 14 | 17 | 20 |
У графикону испод, није тешко пратити зашто се нумерички низ назива "повећање".
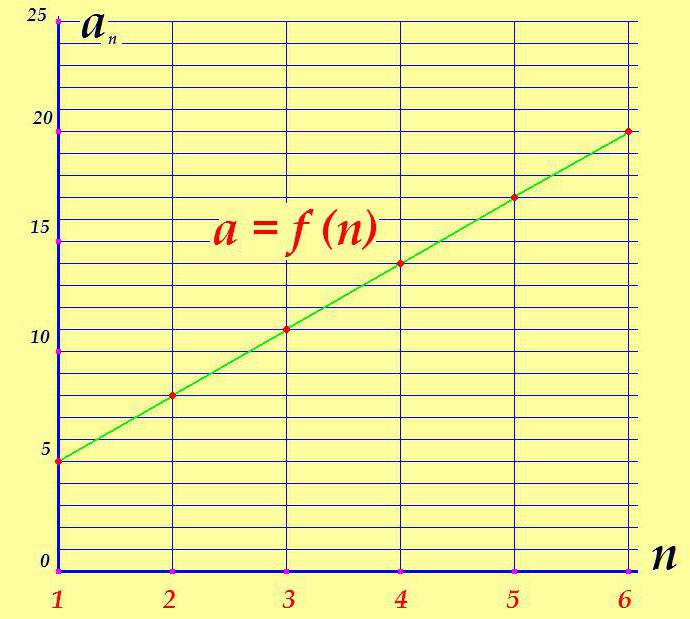
У случајевима када је разлика негативна (д <0), сваки наредни члан ће, из очигледних разлога, бити мањи од претходног, графикон прогресије ће се „спустити“, а аритметичка прогресија ће се означити као опадајући.
Вредност наведеног члана
Понекад је неопходно одредити вредност било ког произвољног термина а н аритметичке прогресије. То можете урадити тако што ћете узастопно израчунати вредности свих чланова аритметичке прогресије, од првог до жељеног. Међутим, такав пут није увијек прихватљив ако је, на примјер, потребно пронаћи вриједност пет-тисућитог или осаммилионитог члана. Традиционална калкулација ће потрајати дуго. Међутим, специфична аритметичка прогресија се може истражити помоћу одређених формула. Постоји и формула за н-ти термин: вредност било ког члана аритметичке прогресије може се одредити као сума првог термина прогресије са разликом прогресије помноженим са бројем члана који се налази, умањен за један.
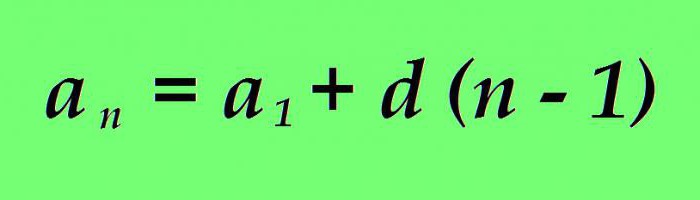
Формула је универзална за напредовање узлазно и силазно.
Пример израчунавања вредности датог члана
Решавамо следећи проблем проналажења вредности н-тог рока аритметичке прогресије.
Услов: постоји аритметичка прогресија са параметрима:
- први рок секвенце је 3;
- разлика броја бројева је 1.2.
Задатак: потребно је пронаћи вриједност од 214 чланова
Решење: да бисмо одредили вредност датог члана, користимо формулу:
а (н) = а1 + д (н-1)
Замењујући у изразу податке из услова проблема имамо:
а (214) = а1 + д (н-1)
а (214) = 3 + 1,2 (214-1) = 258,6
Одговор: 214. члан секвенце је једнак 258.6.
Предности овог метода рачунања су очигледне - целокупно решење не захтева више од 2 линије.
Износ одређеног броја чланова
Веома често, у датој аритметичкој серији, потребно је одредити суму вредности неког сегмента. За ово, такође, нема потребе да се израчунавају вредности сваког члана и онда сумира. Овај метод је примјењив ако је број чланова чија је сума мала. У другим случајевима, погодније је користити следећу формулу.
Збир чланова аритметичке прогресије од 1 до н једнак је збиру првог и н-тог члана помножен бројем члана н и подељен на два. Ако је у формули вриједност н-тог члана замијењена изразом из претходног ставка чланка, добијамо:
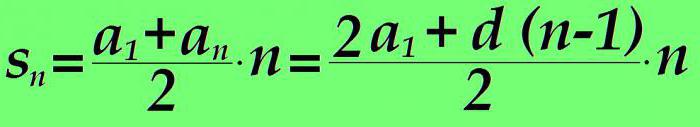
Пример израчунавања
На пример, решите проблем са следећим условима:
- први термин секвенце је нула;
- разлика је 0,5.
Задатак је да се одреди сума чланова серије од 56. до 101. године.
Одлука. Користимо формулу за одређивање количине прогресије:
с (н) = (2 1 а1 + д ∙ (н-1)) / н / 2
Прво, дефинишемо суму вредности 101 члана прогресије, замењујући у формули податке о њиховим условима нашег задатка:
с 101 = (2 + 0 + 0,5 101 (101-1)) /2 101/2 = 2 525
Очигледно, да би се сазнала сума чланова прогресије од 56. до 101., потребно је одузети С 55 од С 101 .
с 55 = (2 + 0 + 0,5 55 (55-1)) /2 55/2 = 742,5
Дакле, сума аритметичке прогресије за овај пример:
с 101 - с 55 = 2 525 - 742,5 = 1 782,5
Пример практичне примене аритметичке прогресије
На крају чланка враћамо се на пример аритметичког низа датог у првом параграфу - таксиметра (бројач такси аутомобила). Размотрите овај пример.
Слетање у таксију (који укључује 3 километра) кошта 50 рубаља. Сваки наредни километар се плаћа по стопи од 22 рубље / км. Удаљеност за путовање је 30 км. Израчунајте трошкове пута.
1. Одбацити прва 3 км, чија је цијена укључена у цијену слијетања.
30 - 3 = 27 км.
2. Даље израчунавање није ништа друго него анализа аритметичких серија бројева.
Број чланова је број пређених километара (минус прва три).
Вредност члана је сума.
Први термин у овом проблему биће једнак а 1 = 50 п.
Разлика прогресије д = 22 п.
број интересовања је вриједност (27 + 1) -ог члана аритметичке прогресије - очитања бројила на крају 27. километра - 27,999 ... = 28 км.
а 28 = 50 + 22 ∙ (28 - 1) = 644
Формуле које описују одређене нумеричке секвенце користе се за израчунавање календарских података за произвољно дуго раздобље. У астрономији, дужина орбите је у геометријској зависности од удаљености небеског тела од звезде. Поред тога, различите нумеричке серије се успјешно примјењују у статистици и другим примијењеним гранама математике.
Други тип броја је геометријски.
Геометријску прогресију карактерише велика, у поређењу са аритметиком, брзина промене. Није случајно да се у политици, социологији и медицини често каже да се процес развија експоненцијално како би се показала висока стопа пропагације феномена, на примјер, болести у епидемији.
Н-ти појам геометријских серија бројева разликује се од претходног по томе што се множи са фиксним бројем - именилац, на пример, први термин је 1, а именилац је 2, редом:
н = 1: 1 = 2 = 2
н = 2: 2 = 2 = 4
н = 3: 4 = 2 = 8
н = 4: 8 = 2 = 16
н = 5: 16 = 2 = 32,
н = 6: 32 = 2 = 64 и тако даље ...
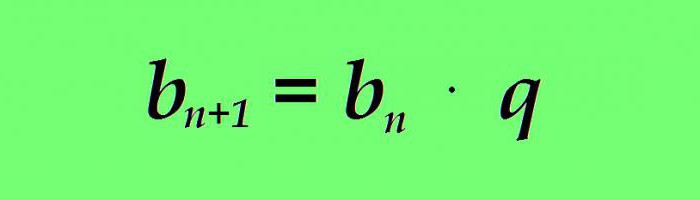
где:
б н - вредност текућег термина геометријске прогресије;
б н + 1 - формула за наредни термин геометријске прогресије;
к је именитељ геометријске прогресије (константни број).
Ако је граф аритметичке прогресије равна линија, онда геометријска црта нешто другачију слику:
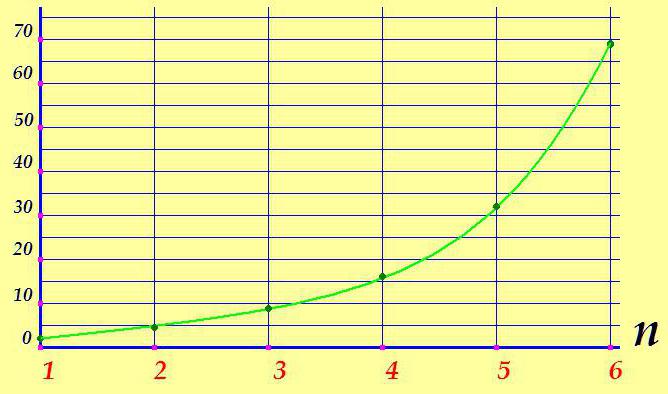
Као иу случају аритметике, геометријска прогресија има формулу за вредност произвољног термина. Сваки н-ти термин геометријске прогресије једнак је производу првог термина имениоцем прогресије до степена н редукованог за један:
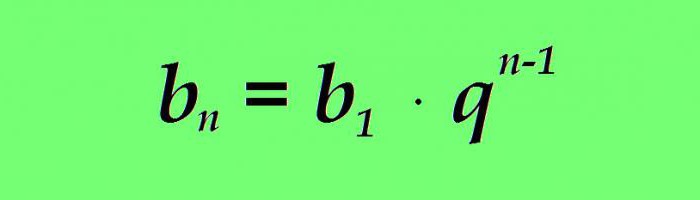
Пример. Имамо геометријску прогресију са првим изразом једнаким 3, а именилац прогресије једнак 1,5. Пронађите 5. члана прогресије
б 5 = б 1 ( к (5-1) = 3 4 1.5 4 = 15.1875
Збир датог броја чланова израчунава се и помоћу посебне формуле. Збир н првих термина геометријске прогресије једнак је разлици производа н-тог термина прогресије по њеном имениоцу, а први термин прогресије подељен имениоцем смањен за један
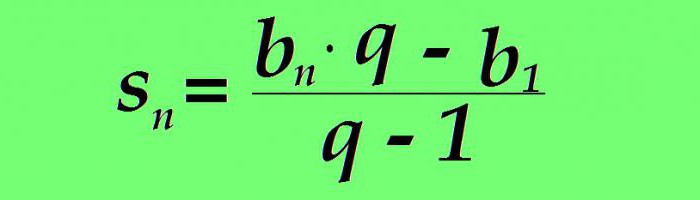
Ако је б н замењен користећи горе наведену формулу, вредност сума н првих чланова разматране серије бројева има облик:
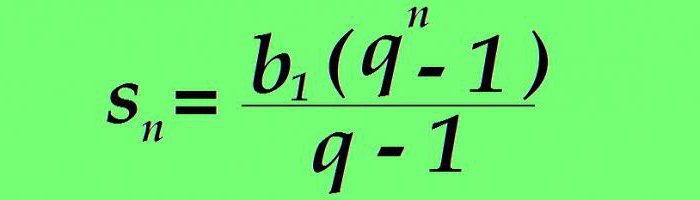
Пример. Геометриц Прогрессион почиње са првим термином једнаким 1. Деноминатор је постављен на 3. Нађи суму првих осам чланова.
с8 = 1 ∙ (3 8 -1) / (3-1) = 3 280