Блок дијаграм: примери, елементи, конструкција. Фловцхартс

Овај чланак ће се бавити примерима дијаграма тока које можете наићи у уџбеницима о рачунарству и другој литератури. Дијаграм тока је алгоритам који рјешава сваки задатак који је додијељен програмеру. Прво треба да одговорите на питање шта је алгоритам, како је он графички представљен, и што је најважније, како га решити, знајући одређене параметре. Треба одмах приметити да постоји неколико типова алгоритама.

Шта је алгоритам?

Ову реч је употребио математичар Мухамед ал-Хорезми, који је живео у периоду од 763-850. Он је особа која је креирала правила за обављање аритметичких операција (њих је само четири). Али ГОСТ из 1974. године, који каже:

Алгоритам је тачан рецепт који дефинише рачунски процес. Штавише, постоји неколико варијабли са датим вредностима које воде до израчунавања до жељеног резултата.

Алгоритам вам омогућава да јасно одредите извођача да обавља стриктно низ акција решити проблем и добити резултат. Развој алгоритма је разбијање једног великог задатка у одређени низ корака. Штавише, програмер алгоритма мора знати све карактеристике и правила за његово креирање.

Алгоритхм феатурес

Укупно, постоји осам карактеристика алгоритма (без обзира на његов тип):

1. Постоји функција за унос почетних података.
2. Постоји закључак одређеног резултата након завршетка алгоритма. Мора се имати на уму да је алгоритам потребан да би се постигао одређени циљ, наиме, да се добије резултат који је директно повезан са изворним подацима.
3. Алгоритам мора имати дискретну структуру типа. Треба да буде представљен у секвенцијалним корацима. Штавише, сваки наредни корак може почети тек након завршетка претходног.
4. Алгоритам мора бити једнозначан. Сваки корак је јасно дефинисан и не дозвољава произвољно тумачење.
5. Алгоритам мора бити коначан - потребно је извршити га у строго одређеном броју корака.
6. Алгоритам мора бити тачан - тражити само право рјешење проблема.
7. Заједница (или масовни карактер) - треба да ради са различитим изворним подацима.
8. Време дато за решавање алгоритма требало би да буде минимално. То одређује ефикасност задатка.

А сада, знајући који алгоритам постоји, можете почети да размишљате како да их напишете. И то није много.

Вербал рецорд

Овај образац се обично користи када се описује поступак за особу: „Иди тамо, не знам где. Донеси нешто, не знам шта.

Наравно, ово је комична форма, али суштина је јасна. На пример, на пример, уобичајена евиденција на прозорима аутобуса: „У случају несреће, извуците кабл, истисните стакло“.

Овде је јасно постављен услов под којим се морају извршити две акције у стриктном редоследу. Али то су најједноставнији алгоритми, постоје и сложенији. Понекад се користе формуле, посебне ознаке, али уз обавезни услов - извођач мора све разумети.

Дозвољено је променити редослед акција ако је потребно да се врати, на пример, на претходну операцију, или да се заобиђе нека наредба под одређеним условима. Истовремено, пожељно је бројати тимове и назначити команду којој се одвија прелазак: „Након што сте завршили све манипулације, поновите тачке од 3 до 5“.

Снимање у графичком облику

Овај унос укључује елементе дијаграма тока. Сви елементи су стандардизовани, сваки тим има одређени графички запис. Посебна наредба мора бити забиљежена унутар сваког блока у обичном језику или математичким формулама. Сви блокови морају бити повезани линијама - они показују тачно који редослед у извршеним наредбама. Заправо, овај тип алгоритма је погоднији за употребу у програмском коду, а не у вербалном.

Писање у програмским језицима

У том случају, ако је алгоритам неопходан да би се задатак ријешио програмом инсталираним на ПЦ-ју, онда га морате написати посебним кодом. За то постоје многи програмски језици. Алгоритам се у овом случају назива програм.

Фловцхартс

Блок дијаграм представља приказ алгоритма у графичком облику. Сви тимови и акције су представљени геометријским облицима (блоковима). Унутар сваке слике се налазе све информације о акцијама које треба извршити. Везе су приказане као нормалне линије са стрелицама (ако је потребно).

За дизајн дијаграма тока алгоритама постоји ГОСТ 19.701-90. Описује поступак и правила за њихово креирање у графичкој форми, као и основне методе рјешавања. Овај чланак представља главне елементе дијаграма тока који се користе у решавању проблема, на пример, у рачунарству. А сада размотримо правила изградње.

Основна правила за креирање дијаграма тока

Постоје такве функције које сваки дијаграм тока треба да има:

1. Мора постојати два блока - "Старт" и "Енд". И у једној копији.
2. Од почетног блока до последње везе треба нацртати.
3. Од свих блокова, осим последњег, линије протока би требале да се угасе.
4. Мора постојати нумерација свих блокова: од врха до дна, с лева на десно. Редни број треба да се стави у горњи леви угао, чиме се прекида ознака.
5. Сви блокови морају бити међусобно повезани линијама. Они треба да одреде редослед којим се акције изводе. Ако се ток креће горе или десно (другим речима, обрнутим редоследом), стрелице се извлаче.
6. Линије су подељене на одлазне и долазне. Треба напоменути да је једна линија за један блок, а за други један.
7. Из почетног блока у шеми, линија протока одлази само зато што је прва.
8. Али коначни блок има само улаз. Ово је јасно приказано у примјерима дијаграма тока који су доступни у чланку.
9. Да би било лакше читати дијаграме тока, долазне линије се извлаче одозго и одлазе одоздо.
10. Присуство празнина у линијама протока. Они су обавезно означени специјалним конекторима.
11. Да би се олакшао дијаграм тока, дозвољено је да се све напомене пишу у коментарима.

Графички елементи дијаграма тока за рјешавање алгоритама приказани су у табели:

Линеарни тип алгоритама

Ово је најједноставнији облик, који се састоји од специфичног низа акција, не зависи од тога који се подаци уносе у почетку. Постоји неколико команди које се извршавају једном и само након што је претходни завршен. Линеарни блок дијаграм изгледа овако:

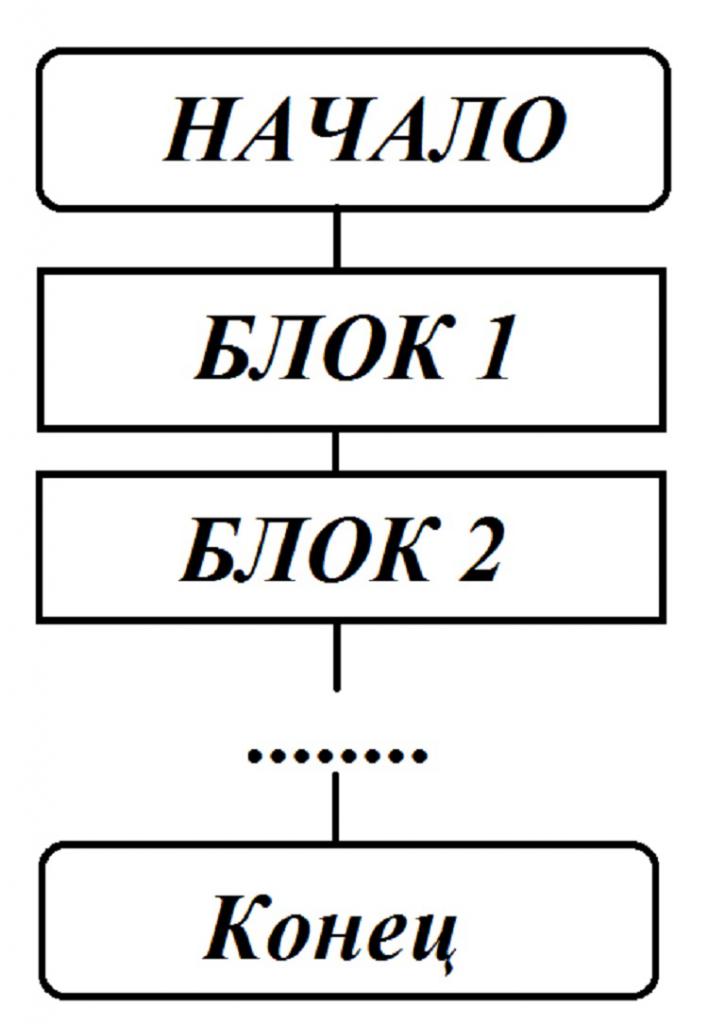
Штавише, везе могу ићи одозго према доле и са лева на десно. Такав дијаграм тока користи се за писање алгоритама за израчунавање помоћу једноставних формула, које немају ограничења на вредности варијабли укључених у формуле за прорачун. Линеарни алгоритам је саставни дио сложених рачунских процеса.

Алгоритми гранања

Дијаграми тока засновани на таквим алгоритмима су сложенији од линеарних. Али суштина се не мења. Алгоритам гранања је процес у којем даљње дјеловање овиси о томе како је увјет испуњен и које је рјешење добивено. Свака линија акције је грана.

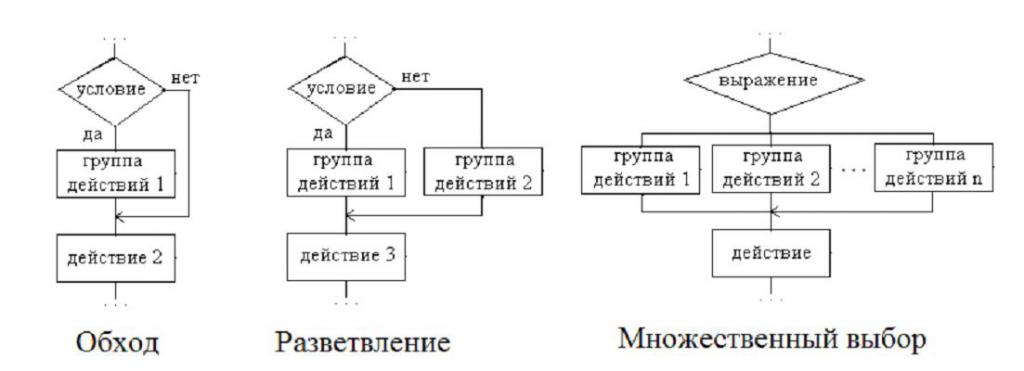
Дијаграми приказују блокове који се називају "Решење". Има два излаза, а унутра је записано логичко стање. Од тога како ће се извршити даље зависи даље кретање у шеми алгоритма. Можете подијелити алгоритме гранања на три групе:

1. "Обилазница" - док једна од филијала нема оператера. Другим ријечима, заобилази се неколико акција друге гране.
2. "Гранање" - свака грана има одређени низ изведених акција.
3. "Вишеструки избор" је вилица у којој постоји неколико грана и свака садржи одређени скуп акција које треба извршити. Постоји једна особина - избор правца директно зависи од тога које вредности су дате за изразе укључене у алгоритам.

То су једноставни алгоритми који се решавају врло једноставно. Пређимо сада на сложеније.

Циклични алгоритам

Све је овде врло јасно - циклични блок дијаграм представља алгоритам у којем се хомогени прорачуни понављају много пута. По дефиницији, циклус је специфична секвенца свих акција које се изводе више пута (више пута). Постоји неколико типова циклуса:

1. Ко зна број понављања акција (они се називају и циклуси са бројачем).
2. У којем је број понављања непознат - са пост-условом и предусловом.

Без обзира на то који тип циклуса се користи за рјешавање алгоритма, он мора имати варијаблу с којом се излаз појављује. Одређује број понављања циклуса. Радни део (тело) циклуса је специфична секвенца акција која се изводи на сваком кораку. Сада ћемо поближе размотрити све типове циклуса који се могу појавити при изради алгоритама и рјешавању проблема рачунарске науке.

Цоунтер Цицлес

На слици је приказан једноставан блок дијаграм у којем постоји циклус са бројачем. Овај тип алгоритма показује да је број понављања датог циклуса унапријед познат. И овај број је фиксиран. У овом случају, варијабла која броји број корака (понављања) се назива бројач. Понекад се у уџбеницима могу наћи и друге дефиниције - параметар циклуса, контролна варијабла.

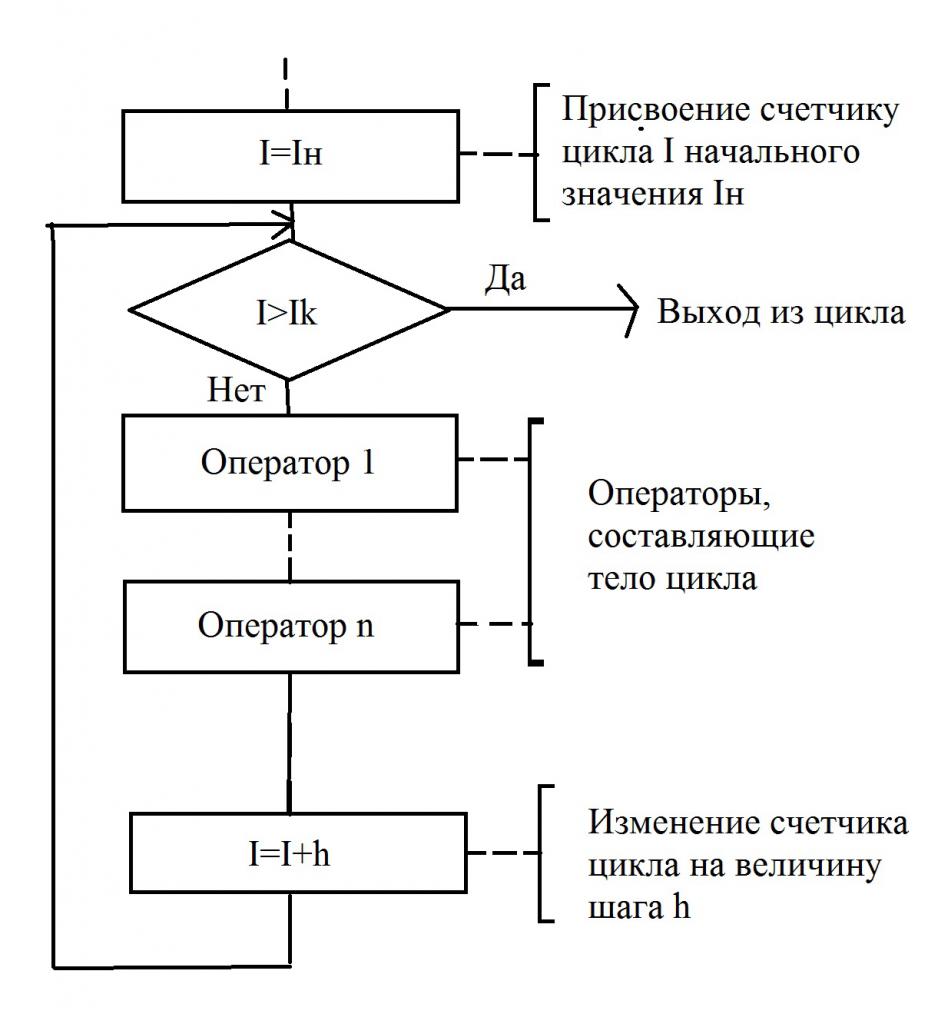
Блок дијаграм врло јасно илуструје како петља ради са бројачем. Пре него што наставите са првим кораком, морате доделити почетну вредност бројачу - то може бити било који број, то зависи од специфичног алгоритма. У случају када је коначна вриједност мања од вриједности бројача, извршит ће се одређена група наредби које чине тијело петље.

Након што је тело извршено, бројач се мења по вредности инкремента бројача, означеног словом х. У случају да је добијена вредност мања од коначне, циклус ће се наставити. И завршиће се само када је коначна вредност мања од бројача петље. Само у овом случају ће се извршити акција која слиједи циклус.

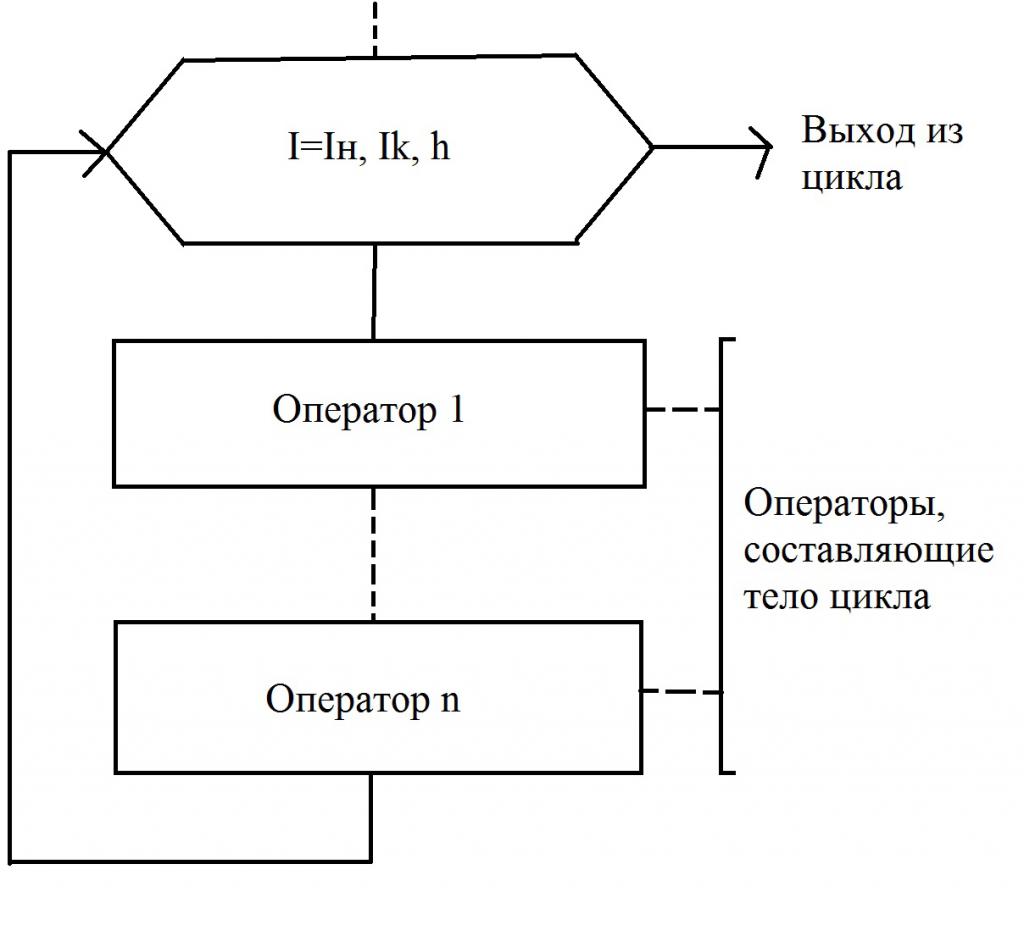
Обично се у нотацији блок дијаграма користи блок који се назива “Припрема”. То се пише у бројачу, а затим се приказују следећи подаци: почетна и коначна вредност, корак промене. У блок дијаграму, то су параметри И н, Ик и х. У случају када је х = 1, величина корака није снимљена. У другим случајевима, то се мора урадити. Неопходно је придржавати се једноставног правила - улазна линија треба да улази одозго. А линија која иде испод (или десно, у зависности од специфичног алгоритма) треба да покаже прелазак на следећег оператера.

Сада сте у потпуности проучили опис дијаграма тока који је приказан на слици. Можете наставити са даљим проучавањем. Када се користи циклус са бројачем, морају бити испуњени одређени услови:

1. Тело не сме да промени (присилно) вредност бројача.
2. Забрањено је преносити контролу извана на оператера тела. Другим речима, у циклус се може ући само од самог почетка.

Предуслови циклуса

Овај тип циклуса се користи у случајевима када број понављања није познат унапријед. Циклус са предусловом је тип алгоритма у коме, непосредно пре него што тело почне да ради, проверава услов под којим је дозвољен прелаз на следећу акцију. Обратите пажњу на то како су приказани елементи блок дијаграма.

У случају када је услов задовољен (изјава је тачна), долази до преласка на почетак тела циклуса. Он директно мења вредност најмање једне променљиве која утиче на вредност скупа услова. Ако се не придржавате овог правила, добићемо "петљу". У случају да се након сљедеће провјере стања извршења тијела петље, испостави да је лажна, тада долази до излаза.

У дијаграмима тока алгоритама, дозвољено је да се не проверава истина, већ лажност почетног стања. У овом случају, циклус ће изаћи само ако је вредност услова тачна. Обе опције су тачне, њихова употреба зависи од тога шта је конкретно погодније користити за решавање одређеног проблема. Овај тип циклуса има једну особину - тело се не може извршити када је услов погрешан или тачан (зависно од варијанте која се користи за решавање алгоритма).

Испод је дијаграм тока који описује све ове радње:

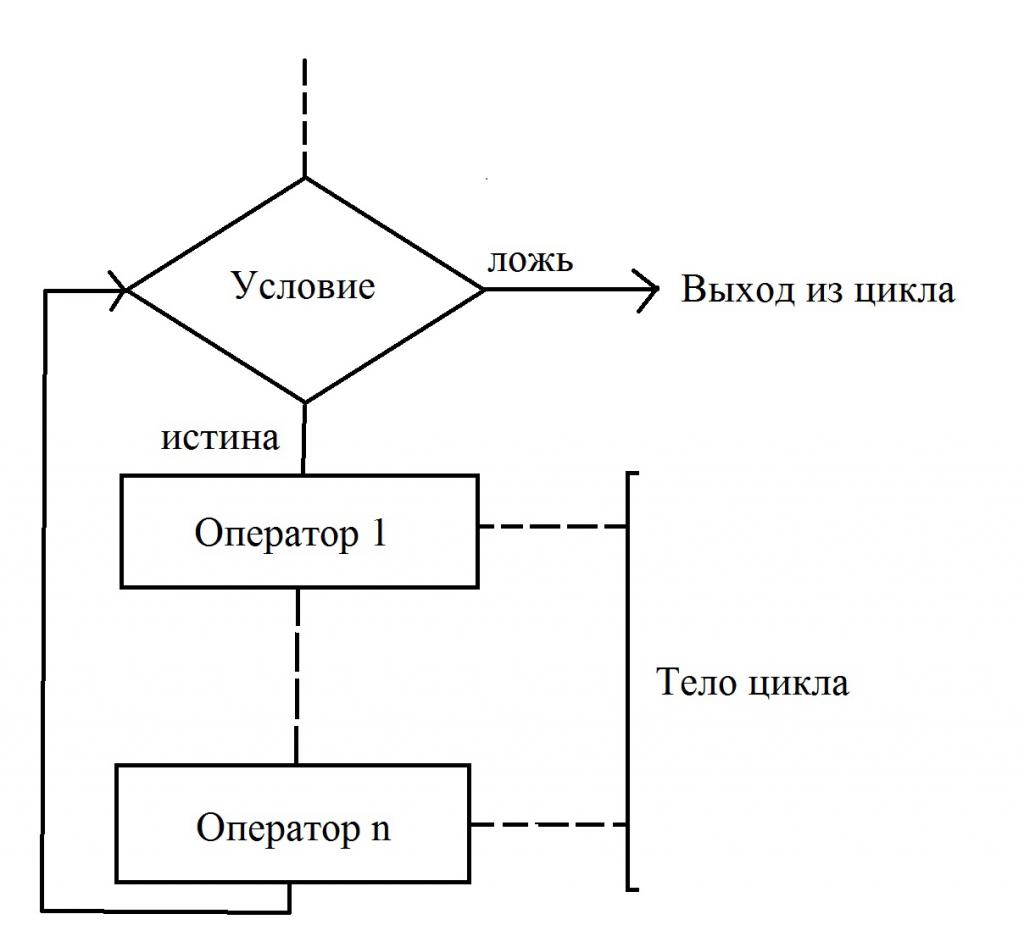
Шта је циклус? са пост-условом?

Ако боље погледате, онда је ова врста циклуса донекле слична претходној. Покушаћемо сами да направимо дијаграм тока који описује овај циклус. Посебност је да број понављања није унапријед познат. А стање се поставља након повлачења из тела. То показује да ће тијело, без обзира на одлуку, бити извршено најмање једном. Ради јасноће, погледајте дијаграм тока који описује стање и изјаве:

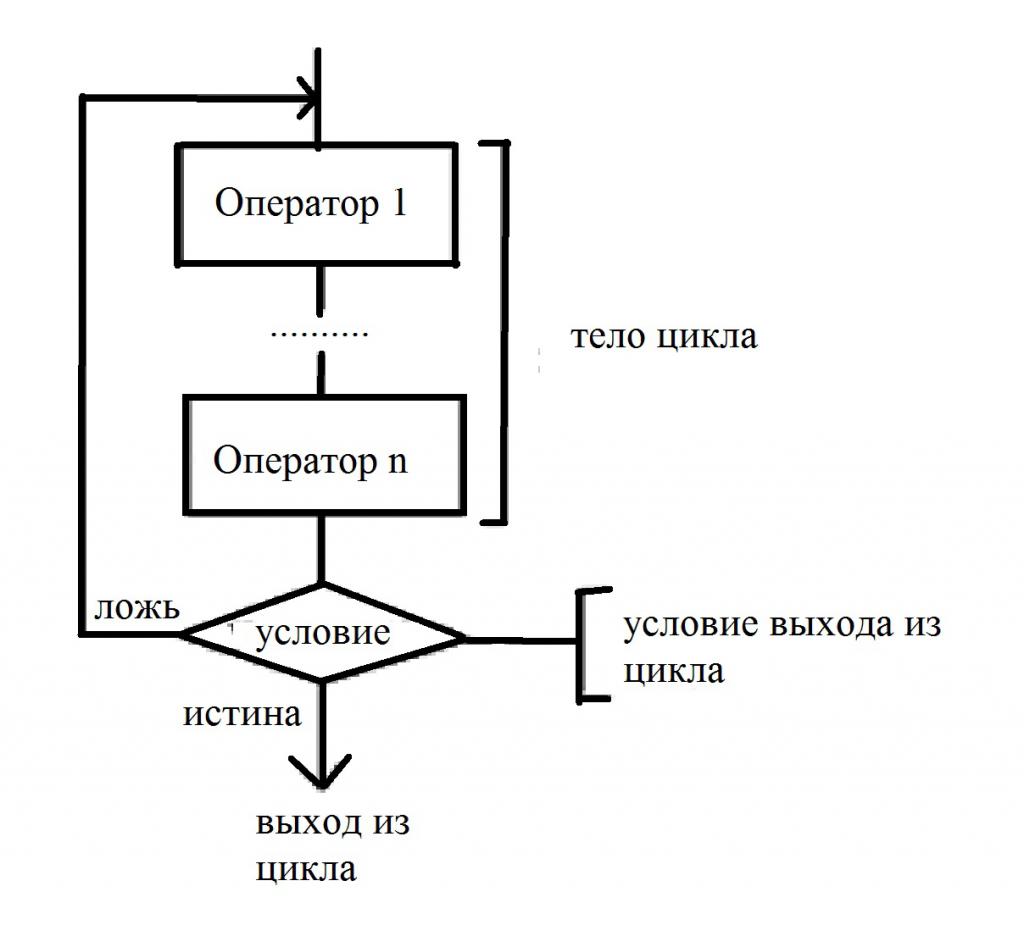
Нема ништа тешко у конструкцији алгоритама са циклусима, довољно је да их разумемо само једном. А сада се окрећемо сложенијим структурама.

Комплексни циклуси

Комплексне су оне конструкције унутар којих постоји један или више једноставних циклуса. Понекад се називају угњежденим. Истовремено, оне структуре које покривају друге циклусе називају се „спољним“. И они који су укључени у дизајн спољашње - унутрашње. Када се изврши сваки корак спољашње петље, унутрашња петља се потпуно помера, као што је приказано на слици:

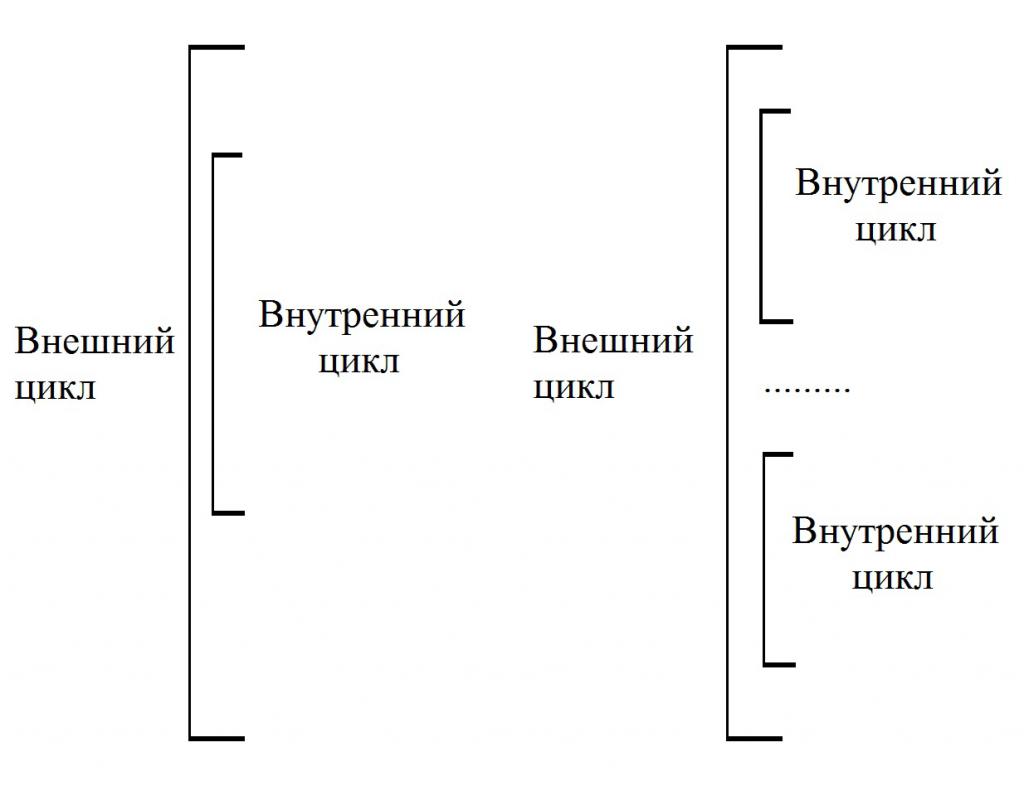
То је све, ви сте прегледали главне карактеристике конструкције дијаграма тока за решавање алгоритама, знате принципе и правила. Сада можете размотрити конкретне примере дијаграма тока из живота. На пример, у психологији, такве конструкције се користе како би особа одлучила питање:

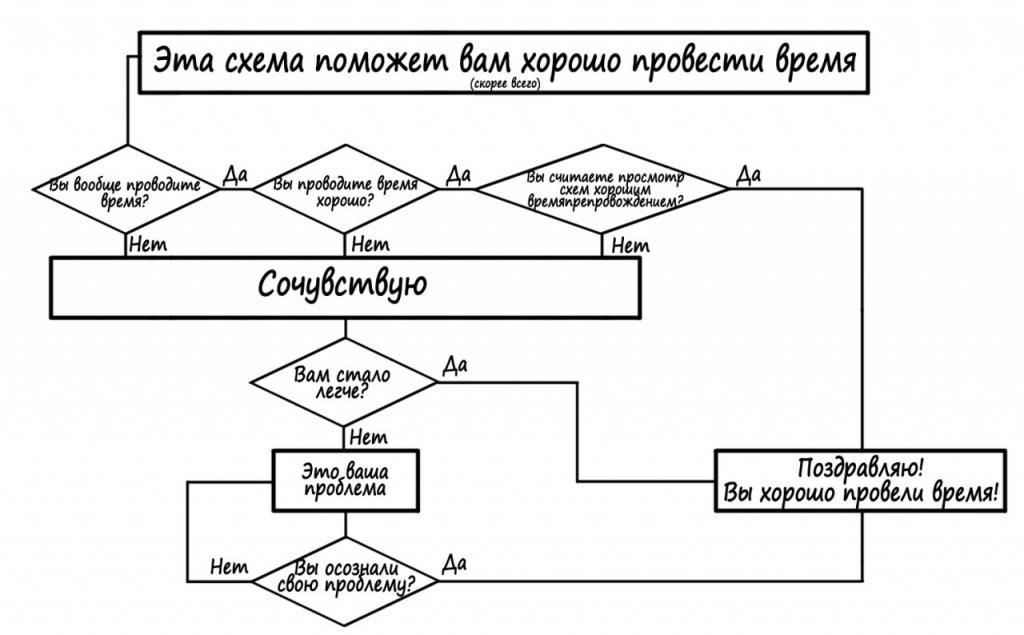
Или примјер из биологије за рјешавање проблема:

Решавање проблема са дијаграмима тока

Сада ћемо погледати примере проблема са дијаграмима тока који се могу наћи у уџбеницима информатике. На пример, дат је блок дијаграм, према којем је решен неки алгоритам:

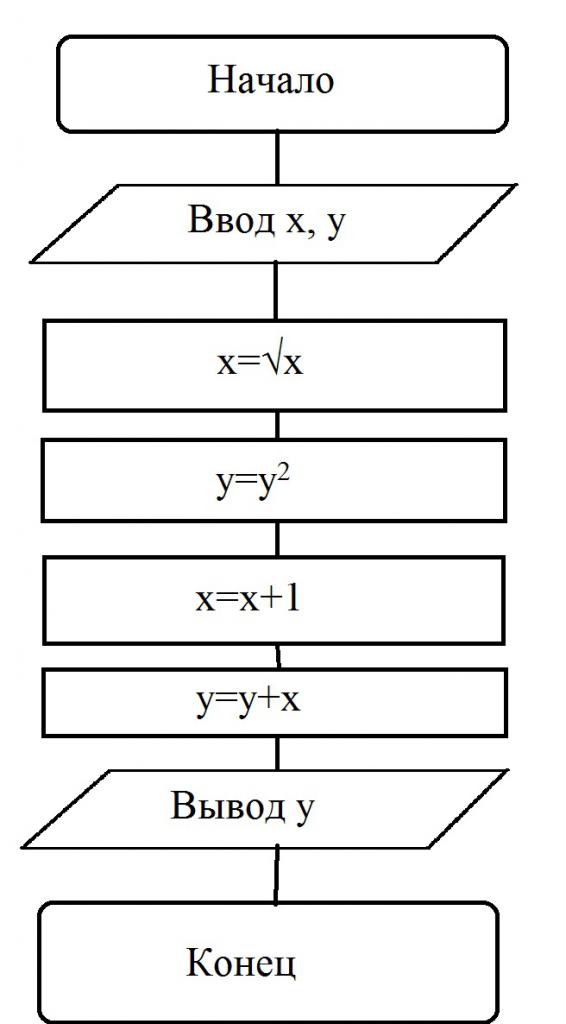
У овом случају, корисник самостално уноси вриједности варијабли. Претпоставимо да је к = 16, а и = 2. Поступак:

1. Унете су вредности к и и.
2. Операција конверзије се изводи: к = =16 = 4.
3. Услов је испуњен: и = и ² = 4.
4. Израчун се врши: к = (к + 1) = (4 + 1) = 5.
5. Следећа варијабла се даље израчунава: и = (и + к) = (5 + 4) = 9.
6. Приказано је решење: и = 9.

У овом примеру, дијаграми тока за рачунарске науке јасно показују како је алгоритам решен. Морате обратити пажњу на чињеницу да су вредности к и и постављене у почетној фази и да могу бити било шта.