Импулс тела: Дефиниција и својства

У свакодневном животу, епитет “импулзиван” се понекад користи за описивање особе која чини спонтане радње. Међутим, неки људи се чак и не сјећају, а значајан дио не зна ни за коју физичку количину се ова ријеч повезује. Шта је скривено под појмом "телесног импулса" и која својства има? Одговоре на ова питања тражили су велики научници као што су Рене Десцартес и Исаац Невтон.

Импулс тела: дефиниција

Као и свака знаност, физика ради са јасно дефинисаним концептима. Тренутно се усваја следећа дефиниција за количину која носи назив телесног импулса: то је векторска величина која је мера (количина) механичког кретања тела.

Претпоставимо да се питање разматра у оквиру класичне механике, тј. Сматра се да се тело креће нормално пре него релативистичком брзином, што значи да је најмање реда величине мања од брзине светлости у вакууму. Тада се импулсни модул тијела израчунава по формули 1 (види слику испод).

Дакле, по дефиницији, ова вредност је једнака производу телесне масе и њеној брзини, са којом је њен вектор ко-усмјерен.

Јединица за мерење импулса у СИ (међународни систем јединица) је 1 кг / м / с.

Одакле долази појам "импулс"?

Неколико векова пре појављивања квантитета у физици механичко кретање тело, сматрало се да је узрок сваког кретања у простору посебна сила - импеус.

Жан Буридан је у 14. веку увео амандмане на овај концепт. Он је предложио да летећа калдрма има подстицај који је директно пропорционалан брзини, која би била непромењена ако не би било отпора ваздуху. У исто време, по мишљењу овог филозофа, тела са већом тежином имала су способност да „задрже“ више такве покретачке силе.

Даљи развој концепта, касније назван импулс, дао је Ренеу Десцартесу, који га је означио ријечима "количина покрета". Међутим, он није узео у обзир да брзина има правац. Зато је теорија коју је он изнио у неким случајевима била у супротности са искуством и није нашла признање.

Чињеницу да количина кретања мора да има и правац, први је нагађао енглески научник Џон Волис. То се догодило 1668. године. Међутим, требало му је још неколико година да формулише чувени закон о очувању импулса. Теоретски доказ ове чињенице, емпиријски установљен, дао је Исак Њутн, који је користио трећи и други закон класичне механике који је он открио, назван по њему.

Импулс система материјалних тачака

Размотримо прво случај када су у питању брзине које су много ниже од брзину светлости. Затим, према законима класичне механике, тотални импулс система материјалне тачке представља векторску количину. Она је једнака суми производа њихових маса при брзини (види формулу 2 на слици горе).

Истовремено, за импулс једне материјалне тачке, они узимају векторску величину (формула 3), која је ко-усмјерена са брзином честице.

Ако говоримо о телу коначне величине, онда је испрва ментално разбијено на мале делове. Дакле, систем материјалних тачака се поново разматра, међутим, његов импулс се израчунава не обичном сумацијом, већ интеграцијом (види формулу 4).

Као што видимо, не постоји временска овисност, стога импулс система, на који не утјечу вањске силе (или је њихов утјецај међусобно компензиран), остаје непромијењен у времену.

Доказ закона о заштити

И даље сматрамо да је тело коначних величина систем материјалних тачака. За сваку од њих, Невтонов други закон је формулисан према формули 5.

Обратите пажњу на чињеницу да је систем затворен. Затим, сумирајући све тачке и примењујући Њутнов Трећи закон, добијамо израз 6.

Дакле, замах затвореног система је константан.

Закон конзервације важи иу оним случајевима када је укупна сума сила које дјелују на систем извана нула. Одавде слиједи једна важна посебна изјава. Наводи да је импулс тијела константан ако нема вањског утјецаја или се компензира утјецај више сила. На примјер, у одсуству трења након штрајка штапом, пак мора одржавати свој замах. Ова ситуација ће се посматрати иако је ово тело погођено гравитација и реакције подршке (леда), будући да су, иако су једнаке величине, усмјерене у супротним смјеровима, тј. међусобно се компензирају.

Пропертиес

Импулс тела или материјалне тачке је адитивна количина. Шта то значи? Све је једноставно: импулс механичког система материјалних тачака састоји се од импулса свих материјалних тачака укључених у систем.

Друго својство ове количине је да остаје непромењено током интеракција које мењају само механичке карактеристике система.

Поред тога, импулс је инваријантан у односу на било коју ротацију референтног система.

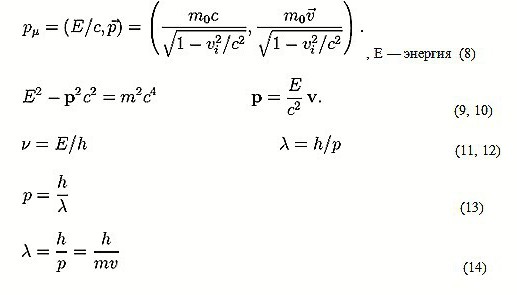
Релативистички случај

Претпоставимо да говоримо о неинтерактирајућим материјалним тачкама које имају брзине од 10 до 8 снаге или нешто мање у СИ систему. Тродимензионални импулс се израчунава по формули 7, при чему под ц значи брзину светлости у вакууму.

У случају када је затворен, закон конзервације момента је истинит. Истовремено, тродимензионални момент није релативистички инваријантна величина, јер је присутна његова зависност од референтног система. Ту је и четвородимензионална опција. За једну материјалну тачку одређује се формулом 8.

Импулс и енергија

Ове количине, као и маса, блиско су повезане једна са другом. У практичним проблемима обично се користе односи (9) и (10).

Одређивање кроз де Броглиеве таласе

1924. године постављена је хипотеза да не само фотони, већ и било које друге честице (протони, електрони, атоми) имају дуалност таласних честица. Његов аутор је био француски научник Лоуис де Броглие. Ако ову хипотезу преведемо на језик математике, онда се може тврдити да је свака честица са енергијом и моментом повезана са таласом фреквенције и дужине изражене формулама 11 и 12, респективно (х је Планкова константа).

Из последње релације, налазимо да је модул импулса и таласна дужина, означена словом „ламбда“, обрнуто пропорционални један другом (13).

Ако се разматра честица са релативно ниском енергијом, која се креће брзином која је несамерљива са брзином светлости, тада се модул импулса израчунава на исти начин као у класичној механици (види формулу 1). Сходно томе, таласна дужина се израчунава према изразу 14. Другим речима, она је обрнуто пропорционална производу масе и брзине честице, односно њеног момента.

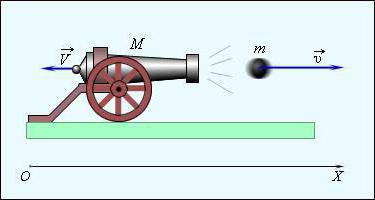
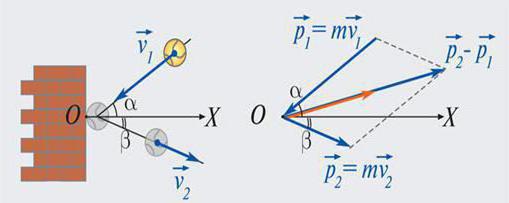
Сада знате да је импулс тела мера механичког кретања и ви сте се упознали са његовим особинама. Међу њима, у практичном смислу, посебно је важно очување права. Чак и људи далеко од физике га посматрају у свакодневном животу. На пример, сви знамо да ватрено оружје и артиљерија дају повратну информацију када се пуца. Закон о очувању импулса јасно показује игру билијара. Помоћу њега можете предвидети правац ширења лопти након штрајка.

Закон је нашао примену у прорачунима неопходним за проучавање утицаја могућих експлозија, у области стварања млазних апарата, у дизајнирању ватреног оружја иу многим другим областима живота.