Круг и његова својства. Цирцумференце ленгтх

Околност у математици је једна од најважнијих и најважнијих фигура. Неопходно је за разне калкулације. Познавање својстава ове фигуре из школског програма свакако ће бити корисно у животу. Обим је потребан за израчунавање великог броја материјала са округлим попречним пресеком. Направите цртеже, направите ограду у близини цвећа - то ће захтевати знање геометријски облик и његова својства.

Концепт круга и његови главни елементи

Слика на равни која се састоји од бројних тачака које се налазе на једнакој удаљености од централне, назива се круг. Сегмент који напушта центар и повезује га са једном од тачака које формирају круг назива се радијус. Акорд је сегмент који повезује пар тачака које се налазе дуж обима круга, између себе. Ако је постављен тако да пролази кроз централну тачку, онда је то и пречник.

Дужина радијуса круга једнака је дужини пречника, преполовљена. Пар неусклађених тачака које се налазе на кругу, деле га на два лука. Ако сегмент са крајевима у овим тачкама пролази кроз централну тачку (тако да је пречник), онда ће формирани лукови бити полукругови.

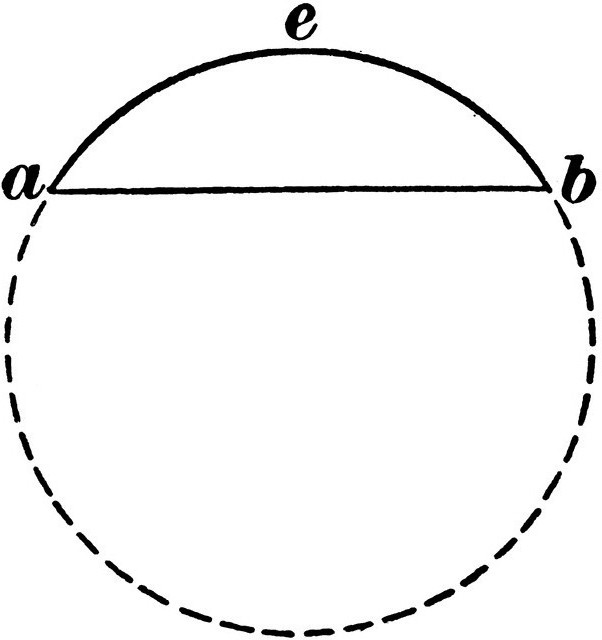
Цирцумференце

Израчун периметра круга се одређује на неколико начина: кроз пречник или кроз радијус. У пракси је утврђено да дужина круга (л) када је подијељена његовим промјером (д) увијек даје један број. Овај број π, који је једнак 3.141692666 ... Израчун се врши по формули: π = л / д. Трансформацијом се добија дужина круга. Формула је следећа: л = πд.

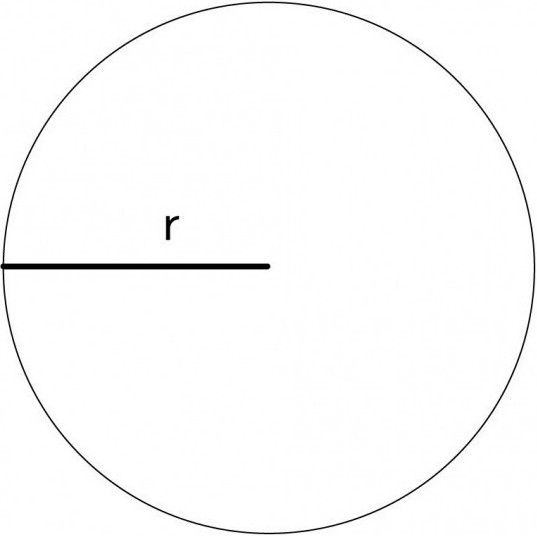
Да бисте пронашли полупречник, примените следећу формулу: д = 2р. Ово је омогућено поделом. На крају крајева, радијус је пола пречника. Када добијемо горе наведене вредности, можемо израчунати дужину круга користећи следећу формулу: л = 2πр.

Основна својства

Подручје круга је увијек веће када се упореди са подручјима других затворених кривуља. Тангента је линија која додирује круг на само једној тачки. Ако га линија пресеца на два места, онда је она секантна. Тачка у којој су два различита круга у контакту један са другим је увек на правој линији која пролази кроз њихове централне тачке. Пресијецање на равнини су такви кругови који имају 2 заједничке точке. Угао између њих се израчунава као угао који тангенте формирају на тачке додира.

Ако кроз тачку која није тачка круга, нацртамо две равне линије које се раздвајају на њу, онда ће угао који они формирају бити једнак разлици у дужинама лукова, преполовљен. Ово правило важи иу супротном случају када су у питању два акорда. Два укрштена акорда формирају угао једнак збиру дужина лукова, преполовљених. У овом углу се бирају лукови у таквој ситуацији и угао насупрот. Оптичко својство круга гласи како слиједи: зраке свјетлости које се рефлектују од зрцала постављених око обода круга, враћају се у његов центар. У том случају, извор светла мора бити инсталиран на централној тачки круга.