Коефицијент корелације и узрочни однос: формуле и њихова интерпретација

Коефицијент корелације је степен повезаности две варијабле. Његов израчун даје идеју о томе да ли постоји зависност између два низа података. За разлику од регресије, корелација не дозвољава предвиђање вриједности величина. Међутим, израчунавање коефицијента је важан корак у прелиминарној статистичкој анализи. На пример, утврдили смо да је коефицијент корелације између нивоа страних директних инвестиција и стопе раста БДП-а висок. То нам даје идеју да је за осигурање добробити неопходно створити повољну климу за стране предузетнике. Не тако очигледан закључак на први поглед!

Корелација и узрочност

Можда не постоји ни једна област статистике која би била тако чврсто утемељена у нашем животу. Коефицијент корелације се користи у свим областима јавног знања. Главна опасност лежи у чињеници да се његове високе вриједности често спекулишу како би се људи увјерили и увјерили у неке закључке. Међутим, у ствари, јака корелација уопште не указује на узрочну везу између количина.

Коефицијент корелације: Пеарсон и Спеарманова формула

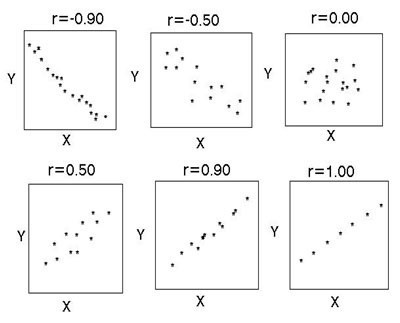
Постоји неколико кључних показатеља који карактеришу однос између двије варијабле. Историјски, први је Пеарсонов коефицијент линеарне корелације. Још је у школи. Развили су га Ц. Пеарсон и Ј. Иул на основу дјела Фр. Галтон. Овај коефицијент вам омогућава да видите однос између рационалних бројева који се рационално мењају. Увек је већи од -1 и мањи од 1. Негативан број означава обрнуто пропорционалну зависност. Ако је коефицијент нула, онда не постоји веза између варијабли. Једнако позитивном броју - постоји пропорционална веза између проучаваних величина. Спеарманов коефицијент корелације ранга вам омогућава да поједноставите израчунавање изградњом хијерархије варијабилних вредности.

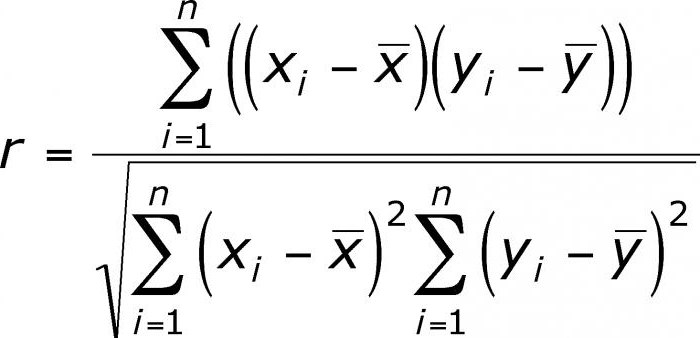
Однос између варијабли

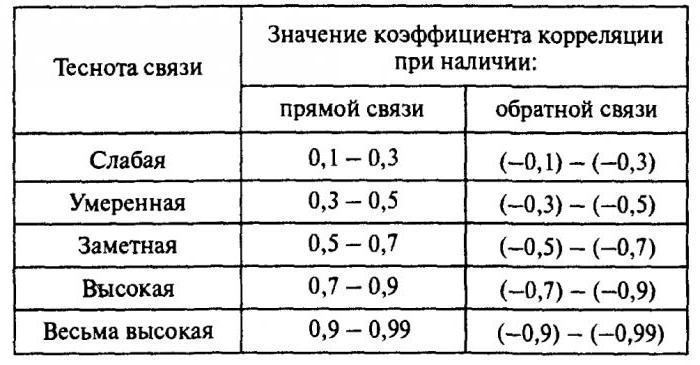
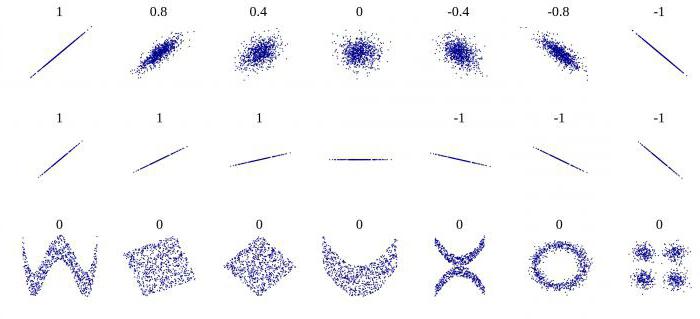
Корелација помаже да се одговори на два питања. Прво, да ли је однос између варијабли позитиван или негативан. Друго, колико је јака овисност. Корелациона анализа је моћан алат помоћу којег можете добити ову важну информацију. Лако је видети да породични приходи и расходи падају и расте пропорционално. Овај однос се сматра позитивним. Напротив, са растом цијена роба, потражња за њом опада. Таква веза се назива негативна. Вриједности коефицијента корелације су у распону од -1 до 1. Нула значи да не постоји веза између вриједности које се истражују. Што је индикатор ближи екстремним вриједностима, јача је веза (негативна или позитивна). Одсуство зависности је назначено коефицијентом од -0,1 до 0,1. Потребно је разумети да таква вредност указује само на одсуство линеарне везе.

Функције апликације

Употреба оба показатеља подложна је одређеним претпоставкама. Прво, присуство јаке везе не имплицира чињеницу да једна количина одређује другу. Можда постоји и трећа количина која дефинише сваку од њих. Друго, високи Пеарсонов коефицијент корелације не указује на узрочну везу између испитиваних варијабли. Треће, показује само линеарну зависност. Корелација се може користити за процену значајних квантитативних података (на пример, атмосферског притиска, температуре ваздуха), а не категорија као што су пол или омиљена боја.

Коефицијент вишеструке корелације

Пирсон и Спеарман су истраживали однос између ове две варијабле. Али како поступити у случају да постоје три или чак више. То је мјесто гдје вишеструки коефицијент корелације долази у помоћ. На пример, на бруто национални производ не утичу само директни стране инвестиције али и монетарне и фискална политика као и ниво извоза. Стопа раста и обим БДП-а резултат су интеракције низа фактора. Међутим, треба разумети да је модел вишеструке корелације заснован на бројним поједностављењима и претпоставкама. Прво, искључена је мултиколинеарност између количина. Друго, претпоставља се да је однос између зависних и варијабли које утичу на њега линеаран.

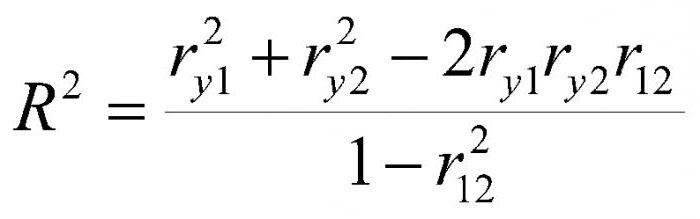
Области коришћења корелационе и регресионе анализе

Овај метод проналажења односа између величина се широко користи у статистици. Најчешће се користи у три главна случаја:

1. Тестирати узрочну везу између вриједности двије варијабле. Као резултат тога, истраживач се нада да ће пронаћи линеарну везу и извући формулу која описује ове односе између величина. Јединице њихових мерења могу бити различите.
2. Да бисте проверили везу између вредности. У овом случају, нико не одређује која је варијабла зависна. Може се испоставити да вриједност обје количине узрокује неки други фактор.
3. Да изведемо једначину. У овом случају, можете једноставно заменити бројеве у њему и сазнати вредности непознате варијабле.

Човек који тражи узрочност

Свест је уређена на такав начин да дефинитивно треба да објаснимо догађаје који се дешавају около. Особа увијек тражи везу између слике свијета у којем живи и информације коју прима. Често мозак ствара ред из хаоса. Он лако може да види узрочну везу тамо где је нема. Научници морају посебно научити да превазиђу овај тренд. Способност процјене односа података је објективно потребна у академској каријери.

Пристрасност медија

Размотрите како се погрешно може тумачити присуство корелацијске везе. Група британских ученика са лошим понашањем је питана да ли њихови родитељи пуше. Тада је тест објављен у новинама. Резултат је показао јаку корелацију између пушења родитеља и прекршаја њихове дјеце. Професор који је водио ову студију чак је предложио да се упозори на пакете цигарета. Међутим, постоји низ проблема са овим закључком. Прво, корелација не показује која је од количина независна. Дакле, може се претпоставити да је зависност родитеља узрокована непослушношћу дјеце. Друго, немогуће је са сигурношћу рећи да се оба проблема нису појавила због неког трећег фактора. На пример, породице са ниским примањима. Треба нагласити емоционални аспект почетних налаза професора који је спровео студију. Био је горљиви противник пушења. Стога не чуди што је резултате свог истраживања интерпретирао на овај начин.

Закључци

Погрешно тумачење корелације као узрочне везе између две варијабле може изазвати срамотне грешке у истраживању. Проблем је у томе што лежи у самој сржи људске свести. Многи маркетиншки трикови су изграђени на овој посебној функцији. Разумевање разлике између узрочности и корелације омогућава рационално анализирање информација како у свакодневном животу тако иу професионалној каријери.