Декомпозиција квадратних тродимената на факторе: примјере и формуле

Декомпозиција квадратних триместера на факторе односи се на школске задатке са којима се сви сусрећу прије или касније. Како то учинити? Која је формула за декомпозицију квадратних фактора? Корак по корак ћемо разумети примјерима.

Општа формула

Декомпозиција квадратних тродимензионалних фактора врши се решавањем квадратне једначине. Ово је једноставан задатак који се може ријешити с неколико метода - проналажење дискриминантног, користећи Виета теорему, постоји и графичко рјешење. Прве две методе проучавају се у средњој школи.

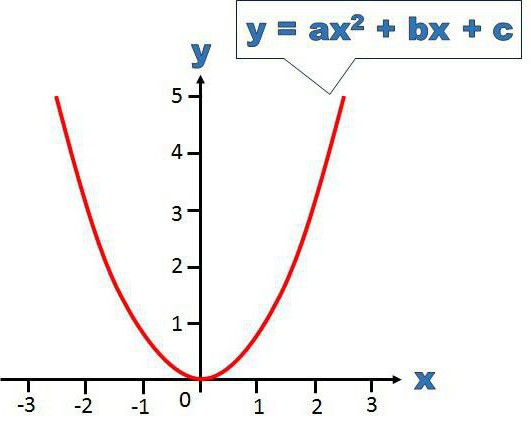
lx ² +kx+n=l(xx ₁ )(xx ₂ ) (1) Општа формула је следећа: лк ² + кк + н = л (кк ₁ ) (кк ₂ ) (1)

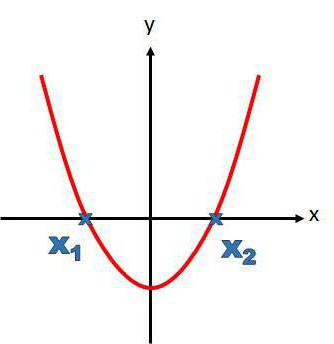
Алгоритам извршења задатка

Да би се извршила факторизација квадратних триномија, потребно је знати Витов теорем, имати рјешење при руци, бити у могућности да нађемо рјешење графички или тражимо корене једнаџбе другог ступња кроз дискриминантну формулу. Ако је дат квадрат триномијума и треба га факторизовати, редослед акција је следећи:

1) Изједначите оригинални израз са нулом да бисте добили једнаџбу.

2) Донесите такве услове (ако постоји таква потреба).

3) Пронађите корење на било који познати начин. Графички метод се најбоље користи ако се унапред зна да су корени цели бројеви и мали бројеви. Мора се имати на уму да је број корена једнак максималном степену једнаџбе, тј. квадратна једначина два корена.

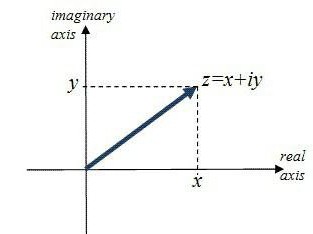
4) Замените вредност к у изразу (1).

5) Запишите декомпозицију квадратних фактора.

Примери

Најзад схватите како се тај задатак обавља, дозвољава праксу. Илустровати факторисање квадратних тродимензионалних примера:

Потребно је проширити израз:

к ² -17к = -32

Приближимо се нашем алгоритму:

1) к ² -17к + 32 = 0

2) смањени су слични термини

3) према формули Виет, тешко је пронаћи корене за овај примјер, јер је боље користити израз за дискриминанту:

Д = 289-128 = 161 = (12.69) ²

к ₁ = 2,155

к ₂ = 14,845

4) Заменити корене које смо нашли у основној формули за разлагање:

(к-2.155) _* (к-14.845)

5) Онда ће одговор бити:

к ² -17к + 32 = (к-2.155) (к-14.845)

Проверите да ли решења пронађена од стране дискриминанта одговарају Виет формулама:

2.155 + 14.845 = 17

14,845 ^. 2,155 = 32

За ове корене се примењује Виет-ова теорема, они су тачно пронађени, што значи да је добијена факторизација такође тачна.

Слично се декомпонује 12к2 + 7к-6.

12к ² + 7к-6 = 0

Д = 337

к ₁ = -7 + (337) ^1/2

к ₂ = -7- (337) ^1/2

У претходном случају, решења су била не-целобројна, али реални бројеви, које је лако пронаћи, пред вама је калкулатор. Сада размотрите сложенији пример у коме ће корени бити комплексни: факторинг к ² + 4к + 9. Према формули за Виета, корени се не могу наћи, а дискриминант је негативан. Коријени ће бити на сложеном плану.

Д = -20

Полазећи од тога, добијамо занимљиве корене -4 + 2и * 5 ^1/2 и -4-2и _* 5 ^1/2 , јер (-20) ^1/2 = 2и * 5 ^1/2 .

Добијамо жељену декомпозицију, замењујући корене у општој формули.

Још један пример: потребно је истаћи израз 23к ² -14к + 7.

=0 Имамо једнаџбу 23к2 -14к + 7 = 0

Д = -448

То значи да су корени 14 + 21,166и и 14-21,166и. Одговор ће бити:

23к2 -14к + 7 = 23 (к-14-21,166и) * (к-14 + 21,166и).

Дајемо примјер, који се може ријешити без помоћи дискриминанта.

Претпоставимо да је потребно проширити квадратну једнаџбу к 2 -32к + 255. Очигледно, може се ријешити дискриминантом, али у овом случају брже је покупити коријене.

к 1 = 15

к 2 = 17

Дакле к 2 -32к + 255 = (к-15) (к-17).