Дијагонална коцка: шта је то и како је пронаћи?

Дијагонала коцке је један од елемената које ћете морати да знате при решавању проблема у стереометрији током завршетка завршног рада из математике за курс основне школе.

Нека теорија коцака

Овај полиедар се директно односи на равне паралелопипеде и призме. Он је посебан случај обоје. У подножју коцке лежи квадрат, а његове бочне ивице су једнаке страни датог квадрата. Тако све три димензије имају исте вриједности.

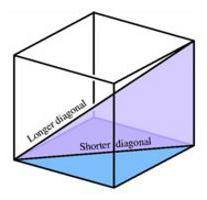
Свих шест лица коцке су квадрати. Дужина сваке од 12 ивица је иста.

У сваком од лица можете нацртати дијагоналу, чију дужину је лако пронаћи помоћу Питагорине формуле. Осим тога, сама коцка има дијагоналу. Има их само четири. Дијагонала коцке је нацртана тако да почиње од врха доње базе. Крај овог сегмента је на врху горње базе, али да се не поклапа са дијагоналом квадрата.

Важне формуле

Они ће морати да унесу исту ознаку. Најчешће је слово "а" страна коцке. "В" је у запремини. "С" и "д" означавају област и дијагоналу. "Р" и "р" радијуси описаних и уписаних сфера.

В = а³ (# 1) се користи за проналажење волумена;

С = а² (# 2) формула за подручје лица;

С = 6а² (№3) је неопходно за израчунавање површине целе површине коцке;

ако желите да знате дијагоналу коцке, формула ће бити таква д = а (3 (# 4);

корисно за тражење радијуса: Р = (а / 2) * √3 и р = а / 2 (бр. 5) и (бр. 6) .

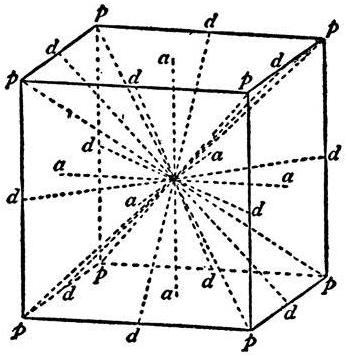
Неколико речи о симетрији коцке

Ово геометријско тело има два типа симетрије: у односу на тачку и ос. Да бисте пронашли прву, морате нацртати дијагоналу коцке, а затим другу да бисте пронашли тачку њиховог пресека. Она ће бити центар симетрије.

Све линије које пролазе кроз ову тачку и које су окомите на лица су оси симетрије.

Примери задатака са испита

Користе се у Делу Б, тј. Тамо где је потребно извршити детаљно решење задатака. Само изаберите одговор овде неће успети. Стога је потребно знати формуле и моћи их примијенити у различитим ситуацијама.

Прва група задатака. Познаје дужину дијагонале коцке. Потребно је израчунати волумен или открити површину.

На пример, позната вредност може бити једнака једној. Затим, да бисте сазнали обим и област, морате користити формуле бр. 1 и 3. Али они говоре о ивици и дају дијагоналу. Мораћете да напишете још једну формулу.

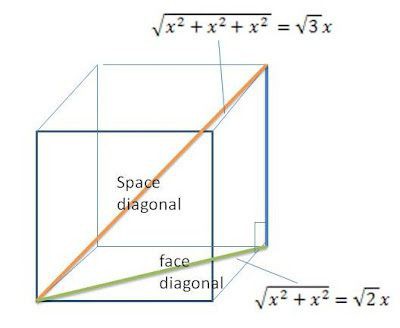
Ако погледате цртеж коцке и дијагоналу нацртану у њему, можете видети које форме правоугаони троугао. Једна од његових ногу се поклапа са ивицом, друга са дијагоналом лица, а дијагонала коцке је хипотенуза.

Тада можемо написати Питагорову теорему: квадрат хипотенузе (д2) је једнак квадрату прве ноге (а ² ), савијеног са квадратом другог (а√2) ² . Након извршених трансформација, испада да је ивица коцке тако повезана са дијагоналом, која је једнака д подељена са квадратним кореном од 3.

Сада можете почети да проналазите ивицу, а затим израчунати волумен и област. У специфичном проблему, а = 1 / =3 = (√3) / 3. Тада је запремина једнака ()3) / 9. Подручје је два.

Друга група задатака. Инверзна претходна, када је подручје или волумен познато, и потребно је израчунати вредност дијагонале коцке.

Примјер је проблем у којем је површина површине позната и једнака је 8. Бит ће потребно користити формулу бр.

Прво морате знати дужину ивице. Она је једнака скуаре роот од парцијалне С до 6. Након замене познате величине, а = √ (8/6) = √ (4/3). Сада остаје да се израчуна дијагонала коцке, квадрирање овог броја и множење на 3. Испада 2.

Трећа група задатака садржи податке о дијагонали лица коцке. Потребно је да препознају волумен или подручје тела. Такође је могућа опција у којој треба да израчунате дијагоналу коцке. У таквим проблемима, расуђивање слиједи исти пут који је разматран у претходним случајевима.