Дискриминантни: примери решења. Како решавати квадратне једначине кроз дискриминацију
Квадратне једначине често се појављују током решавања различитих проблема физике и математике. У овом чланку размотрићемо како да решимо ове једнакости на универзалан начин "кроз дискриминацију". У чланку су наведени и примери коришћења стеченог знања.
О којим једначинама говоримо?
Слика испод приказује формулу у којој је к непозната варијабла, а латински знакови а, б, ц су неки познати бројеви.
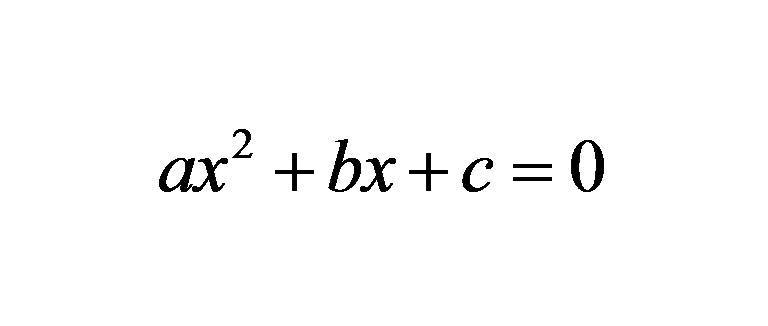
Сваки од ових симбола се назива коефицијент. Као што видите, број "а" стоји испред варијабле к на квадрат. Ово је максимални заступљени израз, тако да се назива квадратна једнаџба. Други назив се често користи: једначина другог реда. Вредност самог себе је квадратни коефицијент (стоји са квадратом променљиве), б је линеарни коефицијент (налази се поред променљиве подигнуте на прву снагу), и коначно, број ц је слободан термин.
Имајте на уму да је тип једначине, који је приказан на слици горе, уобичајен класични квадратни израз. Поред тога, постоје и друге једначине другог реда у којима коефицијенти б, ц могу бити нула.
Када је задатак ријешити разматрану једнакост, то значи да је потребно пронаћи такве вриједности варијабле к које би је задовољиле. Овде прво треба да запамтите следеће: пошто је максимални степен Кс 2, овај тип израза не може имати више од 2 решења. То значи да ако се при решавању једначине нађу 2 вредности к које задовољавају, онда можете бити сигурни да не постоји трећи број, који би заменио са к, једнакост би била истинита. Једначине решења у математици називају га коренима.
Начини решавања једначина другог реда
Решавање ових једначина захтева познавање неких теорија о њима. У школском току алгебре се разматрају 4 различите методе решења. Ми их наводимо:
- усинг фацторизатион;
- користећи формулу за пуни квадрат;
- примену графа одговарајуће квадратне функције;
- помоћу дискриминантне једначине.
Плус, први метод је његова једноставност, али се не може применити на све једначине. Други метод је универзалан, али донекле тежак. Трећи метод се истиче својом јасноћом, али није увек згодан и примјењив. И на крају, употреба дискриминационе једначине је универзалан и прилично једноставан начин да се пронађу корени апсолутно било које једначине другог реда. Према томе, у тексту ћемо га разматрати само.
Формула за добијање корена једначине
Обратимо се општем облику квадратне једначине. Записујемо: а * к² + б * к + ц = 0. Пре коришћења методе решавања "кроз дискриминанта", неопходно је увек свести једнакост на снимљени облик. То јест, мора се састојати од три термина (или мање ако је б или ц 0).
На пример, ако постоји израз: к²-9 * к + 8 = -5 * к + 7 * к², онда бисте прво требали пренети све његове чланове на исту страну једначине и додати изразе који садрже променљиву к у једнаким моћима.
У овом случају, ова операција ће резултирати следећим изразом: -6 * к²-4 * к + 8 = 0, што је еквивалентно једнаџби 6 * к² + 4 * к-8 = 0 (овде смо помножили леву и десну страну једнакости са -1) .
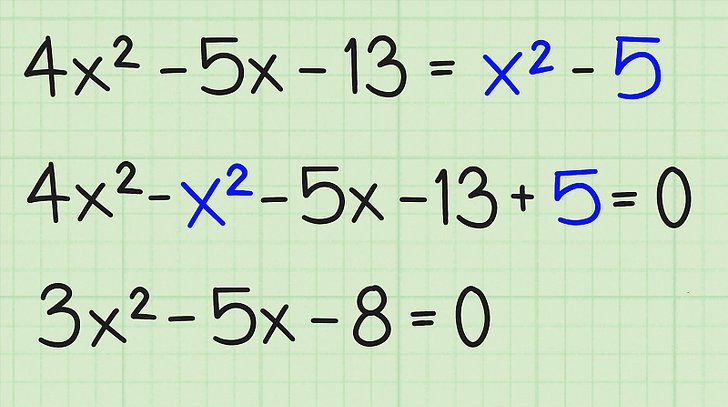
Када се претходни корак научи, онда треба научити да разликујете коефицијенте. Овде је све једноставно: када је к² увек а, када је к 1 б, слободан појам ц је број који није везан за к.
У горњем примеру, а = 6, б = 4, ц = -8. Треба приметити да се сви чланови једнакости који се разматрају увек сабирају међусобно, стога, ако се појави знак "-", то значи да је одговарајући коефицијент негативан, као у овом случају.
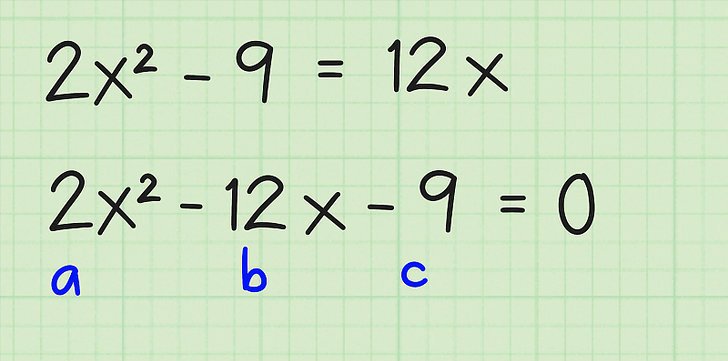
Анализирајући овај тренутак, сада се окрећемо самој формули, која омогућава да се добију коријени квадратне једнаџбе. Изгледа да је то приказано на слици испод.
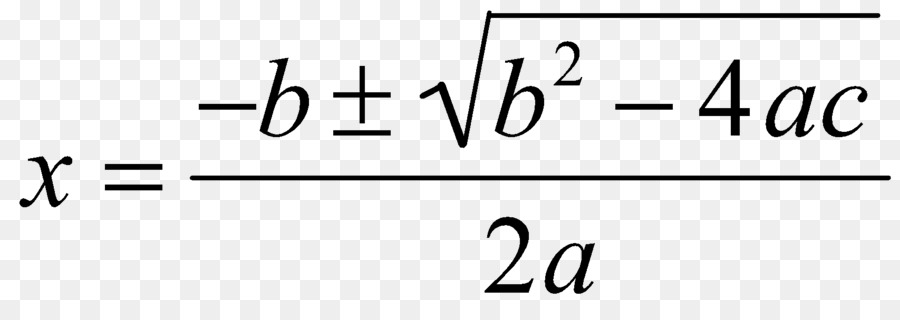
Као што се може видети из овог израза, омогућава вам да добијете два корена (обратите пажњу на знак "±"). Да би се то урадило, довољно је да се замене коефицијенти б, ц и а.
Појам дискриминације
У претходном параграфу дата је формула која вам омогућава да брзо решите било коју једначину другог реда. У њему се израз корена назива дискриминантни, то јест, Д = б²-4 * а * ц.
Зашто је овај дио формуле изолиран, а има чак и своје име? Чињеница је да дискриминант повезује сва три коефицијента једначине у један израз. Потоња чињеница значи да у потпуности носи информације о коренима, што се може изразити на следећој листи:
- Д> 0: једнакост има 2 различита рјешења, оба су реални бројеви.
- Д <0: добијају се и два корена, али оба су комплексна. Овај тип изражавања научио се решавати тек у ренесанси, када су математичари новог времена увели појам "имагинарне јединице".
- Д = 0: једначина има само један корен и прави је број.
У чланку се даље наводе примери дискриминантних квадратних једначина и њихово решење.
Задатак утврђивања дискриминанта
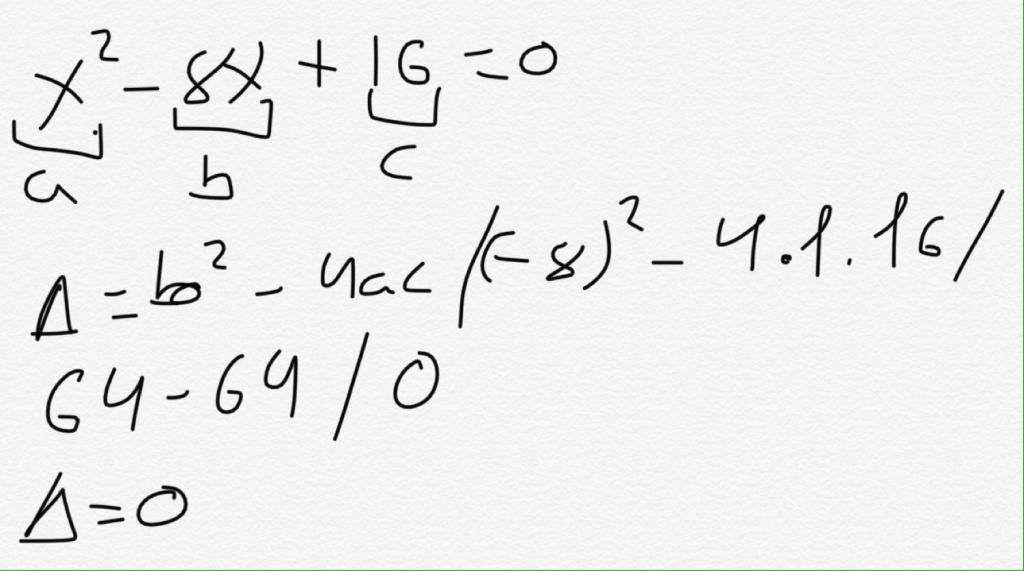
Дајемо једноставан пример како пронаћи дискриминанта. Нека је дата следећа једнакост: 2 * к² - 4 + 5 * к-9 * к² = 3 * к-5 * к² + 7.
Доносимо га у стандардни облик, добијамо: (2 * к²-9 * к² + 5 * к²) + (5 * к-3 * к) + (- 4-7) = 0, одакле стижемо до једнакости: -2 * к² + 2 * к-11 = 0. Ту је а = -2, б = 2, ц = -11.
Сада можете користити формулу за дискриминантну: Д = 2² - 4 * (- 2) * (- 11) = -84. Добијени број је одговор на задатак. Пошто је у примеру дискриминант мање од нуле, можемо рећи да ова квадратна једначина нема правих корена. Његова одлука ће бити само бројеви комплексног типа.
Пример неједнакости кроз дискриминацију
Рјешавамо проблеме нешто другачијег типа: дана је једнакост -3 * к²-6 * к + ц = 0. Потребно је пронаћи вриједности ц за које је Д> 0.
У овом случају, позната су само 2 од 3 коефицијента, стога се не може израчунати тачна вриједност дискриминанта, али се зна да је она позитивна. Потоња чињеница се користи у конструкцији неједнакости: Д = (-6) ²-4 * (- 3) * ц> 0 => 36 + 12 * ц> 0. Рјешење резултирајуће неједнакости води до резултата: ц> -3.
Проверите добијени број. Да бисмо то урадили, израчунали смо Д за 2 случаја: ц = -2 и ц = -4. Број -2 задовољава добивени резултат (-2> -3), одговарајући дискриминант ће имати вриједност: Д = 12> 0. Заузврат, број -4 не задовољава неједнакост (-4 <-3), израчунавамо дискриминант: Д = -12 <0, што је у супротности са стањем проблема.
Дакле, било који бројеви ц већи од -3 задовољавају услов.
Пример решавања једначине
Представљамо проблем, који се не састоји само од проналажења дискриминантног, већ и од решавања једначине. Потребно је пронаћи корене за једнакост -2 * к² + 7-9 * к = 0.
У овом примеру, дискриминант је једнак следећој вредности: Д = 81-4 * (- 2) * 7 = 137. Тада су корени једначине дефинисани као: к = (9 ± √137) / (- 4). То су тачне вредности корена, ако израчунамо корен приближно, онда добијемо бројеве: к = -5,176 и к = 0,676.
Геометријски проблем
Решићемо проблем који ће захтевати не само способност израчунавања дискриминанта, већ и примену вештина апстрактног размишљања и знања, како направити квадратне једначине.
Боб је имао поплун димензија 5 к 4 метра. Дечак је желео да му се шије по ободу од чврсте траке лепе тканине. Колико ће ова трака бити дебела ако се зна да Боб има 10 м² тканине.

Нека трака има дебљину од к м, тада ће површина тканине дуж дуге стране покривача бити (5 + 2 * к) * к, а како су дуге стране 2, имамо: 2 * к * (5 + 2 * к). На краткој страни, површина шивене тканине ће бити 4 * к, пошто су ове стране 2, добијамо вредност 8 * к. Имајте на уму да је вредност 2 к к додата на дугу страну, јер је дужина покривача повећана за овај број. Укупна површина тканине ушивена на деку је 10 м². Дакле, добијамо једнакост: 2 * к * (5 + 2 * к) + 8 * к = 10 => 4 * к² + 18 * к-10 = 0.
За овај пример, дискриминант је: Д = 18²-4 * 4 * (- 10) = 484. Његов корен је 22. Користећи формулу, налазимо жељене корене: к = (-18 ± 22) / (2 * 4) = (- 5; Очигледно, од два корена, само је број 0.5 погодан за стање проблема.
Тако ће трака тканине коју Боб шије за своје ћебе бити широка 50 цм.