Стање равнотеже полуге. Правило тренутака. Једноставни механизми. Задаци и решења
Од памтивијека, човечанство је користило различите механизме који су дизајнирани да олакшају физички рад. Један од њих је полуга. Шта је то, каква је идеја његове употребе, а какво је стање равнотеже полуге, овај чланак је посвећен разматрању свих ових питања.
Када је човечанство почело да примењује принцип полуге?

Тешко је тачно одговорити на ово питање, јер су древни Египћани и становници Мезопотамије већ познавали једноставне механизме још три хиљаде година пре нове ере.
Један од тих механизама је тзв. Полуга-дизалица. Представљао је дугачак ступ, који се налазио на ослонцу. Потоњи је био постављен ближе једном крају пола. Пред крај, који је био даље од референтне тачке, везали су посуду, ас друге су ставили неки противтег, на пример, камен. Систем је подешен тако да је посуда напуњена на пола водила до хоризонталног положаја пола.
Дизалица је служила да подигне воду из бунара, реке или друге депресије до нивоа на коме је особа била. Примјеном мале силе на пловило, особа је спустила на извор воде, посуда је била напуњена течношћу, а затим је, примјењујући малу силу на други крај ступа са противтегом, било могуће подићи назначену посуду.
Легенда о Архимеду и Броду
Сви познају старогрчког филозофа из града Сиракузе, Архимеда, који је у својим списима не само описао принцип рада једноставних механизама (полуга, нагнута даска), већ је резултирао и одговарајућим математичким формулама. До данас, његова фраза остаје позната:
Дај ми ослонац и ја ћу покренути овај свет!

Као што знате, нико му није пружио такву подршку, а Земља је остала на свом мјесту. Међутим, оно што је Архимед могао стварно да помери био је брод. Једна од легенди о Плутарху (дело "Паралелни живот") каже следеће: Архимед у писму свом пријатељу, краљу Хијерону из Сиракузе, рекао је да се може кретати самовољно велика тежина, под одређеним условима. Хиерон је био изненађен таквом изјавом филозофа и замолио га да покаже о чему говори. Архимед се сложио. Једног дана, брод Хиерона, у доку, био је натоварен људима и бачвама испуњеним водом. Филозоф, седећи на удаљености од брода, могао је да га подигне изнад воде, повлачећи конопце, уз мало труда.
Компоненте полуге
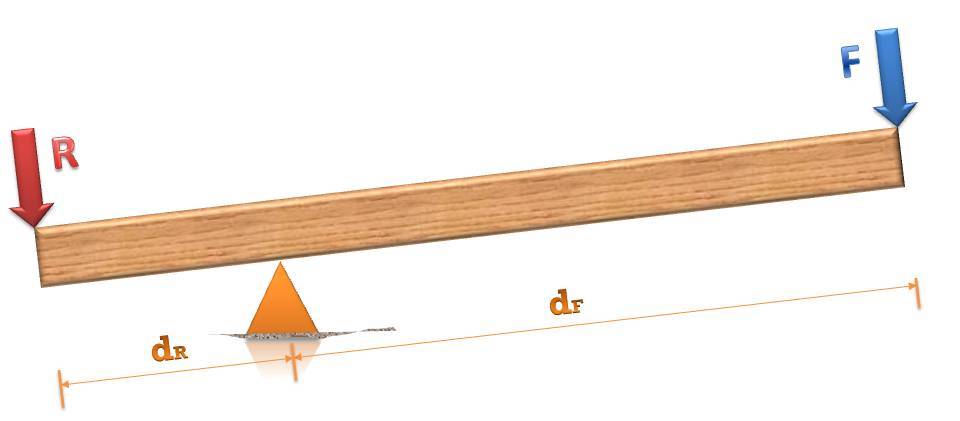
Упркос чињеници да говоримо о прилично једноставном механизму, он још увијек има одређени уређај. Физички, састоји се од два главна дијела: пола или греде и носача. При разматрању истих задатака, пол се сматра предметом који се састоји од два (или једног) крака. Плећка је део пола, који је у односу на ослонац на једној страни. Велику улогу у принципу рада механизма који се разматра управо је дужина рамена.
Када разматрамо полугу у раду, онда постоје два додатна елемента: примењена сила и снага за супротстављање. Први настоји да покрене предмет који ствара силу опозиције.
Стање равнотеже полуге у физици
Упознајући се са уређајем овог механизма, представљамо математичку формулу, помоћу које можемо рећи која рука полуге ће се померати у ком правцу или, обрнуто, цео уређај ће бити у мировању. Формула има форму:
Ф 1 * л 1 = Ф 2 * л 2 ,
где су Ф1 и Ф2 силе деловања и реакције, односно, л1 и л2 су дужине кракова на које се те силе примењују.
Овај израз вам омогућава да истражите услове равнотеже полуге која има ос ротације. Дакле, ако је раме л 1 веће од л 2 , онда је за балансирање силе Ф 2 потребна мања вредност Ф 1 . Напротив, ако је л 2 > л 1 , онда да би се супротставила сила Ф 2 , мораћете да причврстите велики Ф1. Ови закључци се могу добити поновним писањем горе наведеног израза у следећем облику:
Ф 1 / Ф 2 = л 2 / л 1 .
Као што се може видети, силе укључене у процес формирања равнотеже су инверзно повезане са дужином кракова полуге.
Који је добитак и губитак када се користи полуга?
Важан закључак произилази из горњих формула: уз помоћ дуге руке и малог напора, предмети са великом масом могу се померати. То је истина, и многи могу помислити да употреба полуге доводи до добитка у раду. Али није. Рад је количина енергије која се не може створити из ничега.
Анализирамо рад једноставне полуге која има два стврдњавања л 1 и л 2 . Претпоставимо да на крају рамена л 2 постоји тежина тежине П (Ф2 = П). На крају другог рамена, особа примењује силу Ф 1 и подиже то оптерећење на висину х. Сада, израчунајмо рад сваке силе и изједначимо добијене резултате. Добијамо:
Ф 1 к = Ф 2 * х.
Сила Ф 2 је деловала дуж вертикалне путање дужине х, а Ф 1 је такође деловала дуж вертикале, али је већ била причвршћена за другу руку, чији се крај померао непознатом величином к. Да би га пронашли, потребно је у последњем изразу заменити формулу везе између сила и кракова полуге. Изражавајући к, имамо:
к = Ф 2 * х / Ф 1 = л 1 * х / л 2 .
Ова једнакост показује да ли л 1 > л 2 , затим Ф 2 > Ф 1 и к> х, тј. Примењујући малу силу, можете подићи терет са великом тежином, али морате померити одговарајућу полугу (л 1 ) на већу. удаљености. Напротив, ако је л 1 <л 2 , онда Ф 2 <Ф 1 и к <х, то јест, тежина одређене тежине може се подићи на већу висину х померањем рамена л 1 на мању амплитуду, али морате применити довољно велику силу Ф 1 . У првом случају добија се појачање снаге, у другом на начин или брзином.
Дакле, полуга не користи у раду, већ омогућава само редистрибуцију у корист мање примењене силе, или у корист веће амплитуде кретања објекта. Општи филозофски принцип функционише у предмету физике о којој се расправља: сваки добитак се компензира одређеним губитком.
Врсте полуга
У зависности од тачака примене силе и позиције носача, разликују се следећи типови овог механизма:
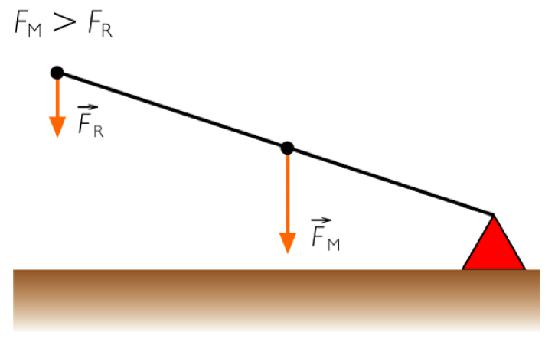
- Прва врста: упориште је између двије силе Ф 1 и Ф 2 , дакле, дужина руку ће одредити што даје такву предност. Пример су обичне маказе.
- Друга врста. Овде се сила против које се обавља посао налази између подршке и примењене силе. Овакав тип конструкције значи да ће увек давати добитак у снази и губитак путовања и брзине. Његов пример је баштенски аутомобил.
- Трећа врста. Последња опција, која остаје да се оствари у овом једноставном дизајну, је положај примењене силе између ослонца и силе отпора. У овом случају, добитак на путу, али губитак је на снази. Један примјер би био пинцета.

Концепт тренутка силе
Разматрање било каквих проблема у механици, који укључују концепте оси или тачке вешања, врши се коришћењем правила момента силе. Пошто је ослонац полуге такође осовина (тачка) око које се систем ротира, момент силе се такође користи за процену равнотеже овог механизма. Под овим се подразумева количина у физици, једнака производу рамена и делујуће силе, односно:
М = л * Ф.
С обзиром на ову дефиницију, стање равнотеже полуге може се преписати на следећи начин:
М 1 = М 2 , где М 1 = л 1 * Ф 1 и М 2 = л 2 * Ф 2 .
Тренутак М је адитиван, што значи да се укупни моменат силе за дотични систем може добити уобичајеним додавањем свих тренутака М и који дјелују на њега. Међутим, треба узети у обзир њихов знак (сила која узрокује да се систем окрене у смјеру супротном од казаљке на сату ствара позитиван тренутак + М, и обрнуто). Са тим речима, правило момената за полугу која је у равнотежи ће изгледати овако:
М 1 - М 2 = 0.
Полуга губи равнотежу када М 1 = М 2 .
Где се користи принцип левериџа?
Већ смо навели неке примјере употребе овог једноставног и добро познатог механизма из античких времена. Ево само неколико додатних примјера:
- Клијешта: полуга 1. врсте, која вам омогућава да направите огромне напоре због мале дужине рамена л 2 на којима се налазе зуби алата.
- Поклопци отварача лименке и боце: то је полуга 2. врсте, тако да увек даје добитак у напору.
- Шипка за риболов: полуга 3. врсте, која вам омогућава да помичете крај штапа за риболов са плутачем, сјенилом и куком за велике амплитуде. Губитак у овом случају се осјећа када рибар тешко може извући рибу из воде, чак и ако њена тежина не прелази 0,5 кг.

Човек сам са својим зглобовима, мишићима, костима и тетивама је живописан пример система са много различитих полуга.
Решавање проблема
Стање равнотеже полуге о којој се говори у чланку користи се за решавање једноставног проблема. Неопходно је израчунати приближну дужину полуге, примјењујући напор до краја којег је Архимед могао да подигне брод, како га Плутарх описује.

Да бисмо то решили, уводимо следеће претпоставке: узмемо у обзир грчку трирему од 90 тона са помаком и претпоставимо да је подршка полуге била 1 метар од центра масе. Како је Арцхимедес, према легенди, лако могао да подигне брод, претпоставићемо да је у ту сврху применио силу која је износила половину његове тежине, односно око 400 Н (за масу од 82 кг). Затим, примењујући стање равнотеже полуге, добијамо:
Ф 1 * л 1 = Ф 2 * л 2 => л 1 = Ф 2 * л 2 / Ф 1 = м * г * л 2 / Ф 1 = 90000 * 9,81 * 1/400 ≈ 2,2 км.
Чак и ако повећамо силу која се примењује на вредност тежине самог Архимеда и доносимо подршку још два пута, онда ће дужина рамена бити око 500 метара, што је такође велика вредност. Највероватније, легенда о Плутарху је претеривање да би се показала ефикасност полуге, а Архимед није заправо подигао брод изнад воде.