Теорија графова: Основне дефиниције

Теорија графова је грана математике која се користи у рачунарству и програмирању, економији, логистици и хемији.

Шта је граф

Графички системи се често користе за описивање структуре система. Елементи у њима су представљени круговима, тачкама, квадратима, итд., А везе између елемената су линије или стрелице. Истовремено, није важно ни како су елементи приказани, ни дужина или облик линија важни - само који су елементи повезани. Граф је, дакле, пар облика (А, М), где је А коначан скуп врхова, а М је скуп ивица - линија које повезују неке врхове.

Основни концепти теорије графова

За усмерени график или диграф (види слику испод), ивице су оријентисане, називају се луковима и приказане су стрелицама. Лук се може означити уређеним паром врхова које повезује - почетни и коначни.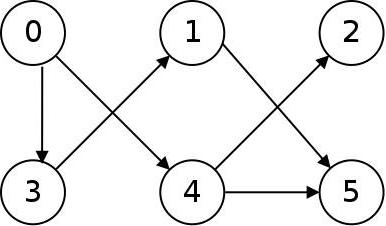

За неусмерени график (види слику испод), ивице су представљене линијама без оријентације. У складу с тим, пар врхова који се повезује је неуређен. Оба ова врха су крајеви ивице.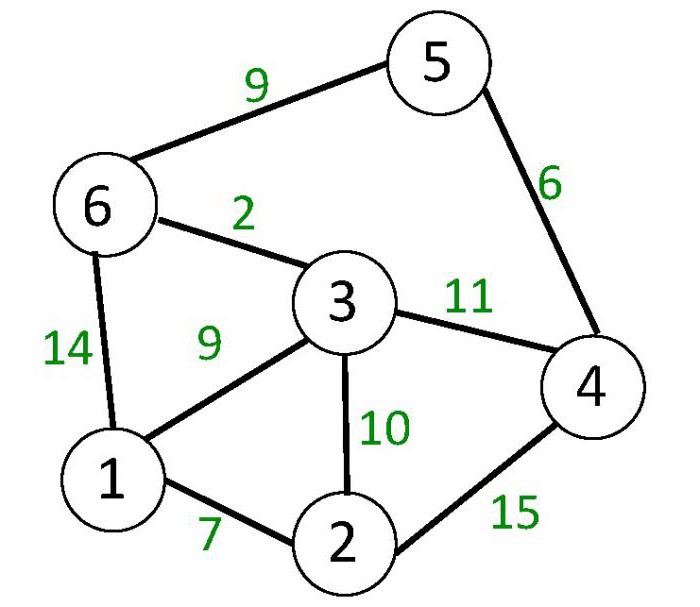

Ако су тацке а и б крајеви ивице (или поцетка и краја лука) графа, онда цемо реци да су врхови а и б упадљиви на ову ивицу (лук), а и ивица (лук) је инцидент у врховима а и б. Ако су врхови а и б крајеви ивице, онда се они (а и б) називају сусједни.

Најчешће разматрају графиконе чији су рубови истог типа - оријентисани или не.

Ако рубови имају исти почетак и крај, онда се они називају вишеструким ивицама, а граф у којем су присутни назива се мултиграф.

Теорија графова такође користи концепт "петље" - ивице која иде и поставља се на исти врх. Граф у коме се налазе петље се назива псеудограф.

Најчешћи не-оријентисани графови који немају више ивица и немају петље. Такви графикони се зову обични. Они немају вишеструке ивице, тако да можете идентификовати ивицу и одговарајући пар врхова.

Сваки врх диграфа се карактерише:

• Неразвијеност. Ово је број лукова који излазе из њега.
• Неразвијеност. Ово је број лукова који улазе у дату тачку.

Збир полу-степени уноса диграфа, као и сума полу-степени исхода, једнаки су укупном броју лукова графа.

У неусмереном графу, сваки врх је окарактерисан степеном његовог врха. Ово је број ивица које су инцидентне на врху. Укупна сума степени у врховима графикона је број ивица помножен са два: свака ивица ће дати допринос који је једнак два.

Врх са степеном 0 се назива изолован.

Висећи врх је врх са степеном 1.

Теорија графова назива празан графикон у коме нема ниједне ивице. Комплетан граф је обични графикон у којем су 2 врха суседна.

Вагани графикони су графикони, којима су одмах додељени врхови или ивице (лукови) или оба врха и ивице (лукови), неки бројеви. Називају се теговима. Друга слика приказује неусмерени графикон чије су ивице пондерисане.

Цоунтс: исоморпхисм

Појам изоморфизма користи се у математици. Конкретно, теорија графова дефинише је на следећи начин: два графика У и В су изоморфна ако постоји бијекција између скупова њихових врхова у овим графиконима: свака два врха у графикону У су повезана ивицом ако и само ако је иста у графу В вертицес (које се могу називати другачије). На доњој слици приказана су два изоморфна графика, у којима се између вертикала обојених у истим бојама у првом и другом графикону налази горе описана бијекција.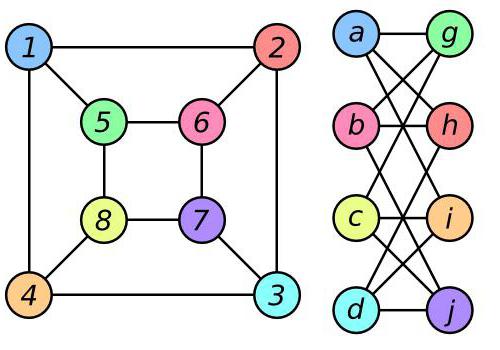

Путеви и циклуси

Пут у неусмереном или оријентисаном графу је низ ивица, где свака следећа почиње на врху у коме се завршава претходни. Једноставна стаза је она у којој су сви врхови, искључујући, можда, почетни и коначни, и ивице различити. Циклус у диграфу је путања чији се почетни и коначни врхови поклапају и која укључује најмање једну ивицу. Циклус у неусмереном графу је путања која садржи најмање три различите ивице. У другој слици, циклус је, на пример, путања (3, 1), (6, 3), (1, 6).

Теорија графова у програмирању користи се за конструкцију граф-шема алгоритама.