Како направити графикон линеарних функција. Примери
Да би се схватило како исцртати линеарну функцију, важно је разумети саму суштину функције. Функција је модел зависности промена једног параметра од другог.
Тема функционалних зависности традиционално се отвара линеарном функционалном зависношћу. Линеарна је најједноставнија зависност. Граф линеарне функције је раван.
Живот и функција
У животу, линеарне зависности се обично налазе у идеалним вештачким процесима, промене у којима се претпоставља да су трајне. На пример, када особа иде негде са константном брзином.
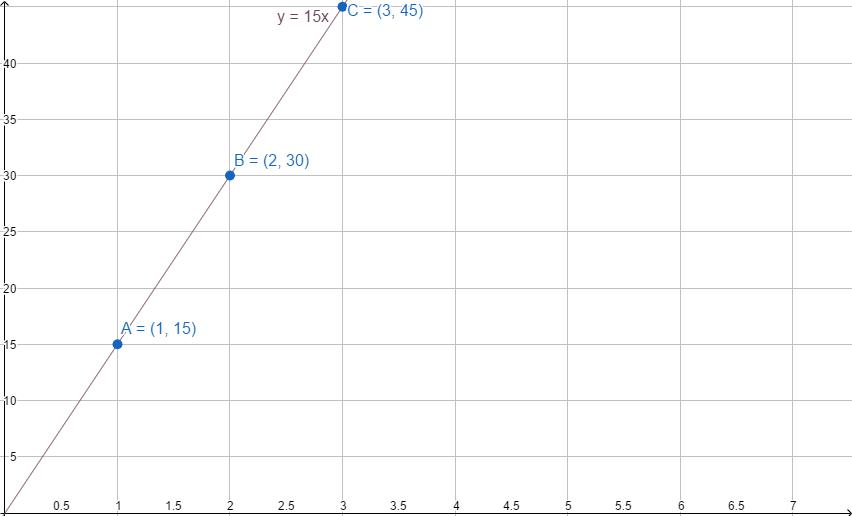
Удаљеност коју ће особа возити бициклом варираће линеарно у зависности од броја сати путовања. Ако вози 15 километара за сат времена (тачка А), онда ће за два сата возити 30 километара (тачка Б), за три сата - 45 (тачка Ц).
Зависност је описана једнаџбом и = 15к. Како исцртати линеарну функцију у овом случају?
- пронаћи координате тачака које су решење једначине;
- гради их на координатној равни;
- повежите ове тачке са линијом.
Опис алгоритма
Тражење координата тачака које су решења једначине своди се на проналажење две тачке које јединствено дефинишу линију. Иако је довољно изабрати двије различите вриједности к и пронаћи одговарајуће вриједности и, могу се наћи три пара вриједности за самоконтролу. То ће вам омогућити да брзо утврдите могућу грешку у прорачуну. Често је прва вредност к изабрана да буде нула.
| и = 15к | (0, 0) | (1, 15) |
| к = 0 | к = 1 | |
| и = 15 × 0 | и = 15 × 1 | |
| и = 0 | и = 15 |
Друга вредност к за велики к је боље изабрати поред прве. У супротном, биће присутан јак расипање вредности и и к, на пример, код к = 4 у разматраној једначини, и = 60. У сваком случају, пре цртања линеарне функције на пронађеним тачкама, бира се скала.
| и = 25 к | (0, 0) | (1, 25) |
| к = 0 | к = 1 | |
| и = 25 × 0 | и = 25 × 1 | |
| и = 0 | и = 25 |
Коефицијент за к
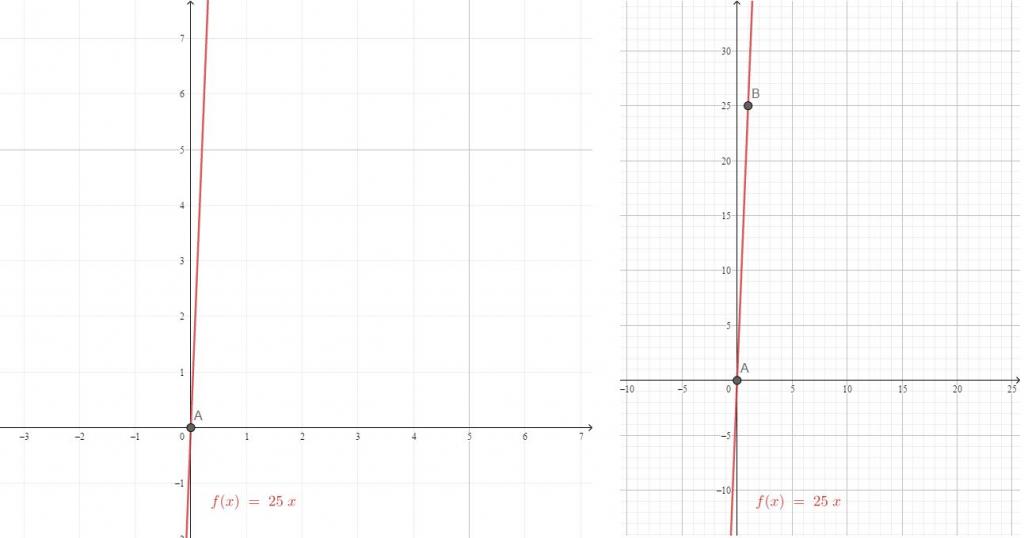
Једнаџба линеарне функције је облика и = кк + б. У зависности од промене коефицијента за непознато, природа графа линеарне функције и = кк такође се мења.
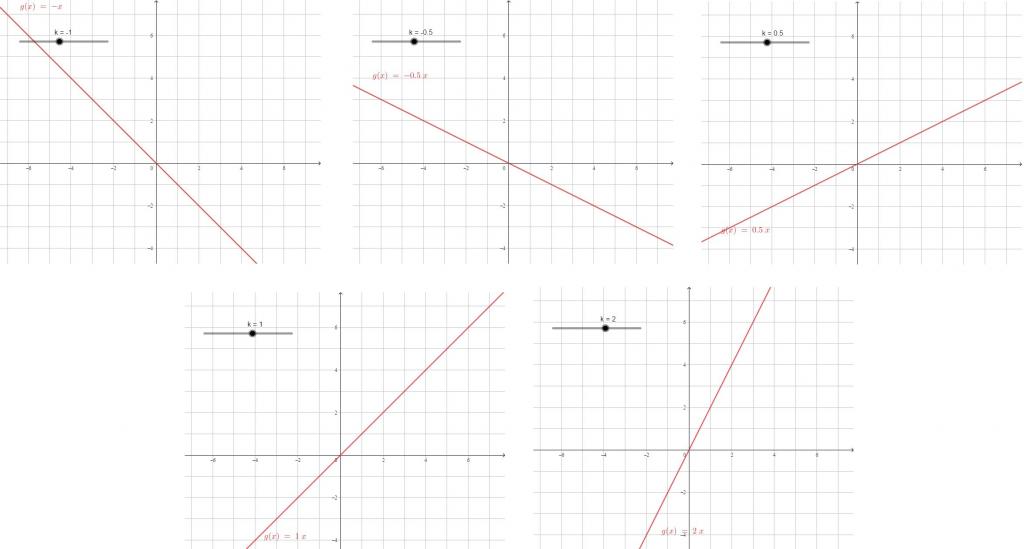
Што је већи коефицијент модула, то је већа стрмина праве линије, то је за исту промјену вриједности к јача вриједност промјене и. Коефицијент к је коефицијент пропорционалности.
Фрее ратио
Слободни коефицијент је константа која не зависи од промена вредности к. То показује где се линија укршта са ОИ.
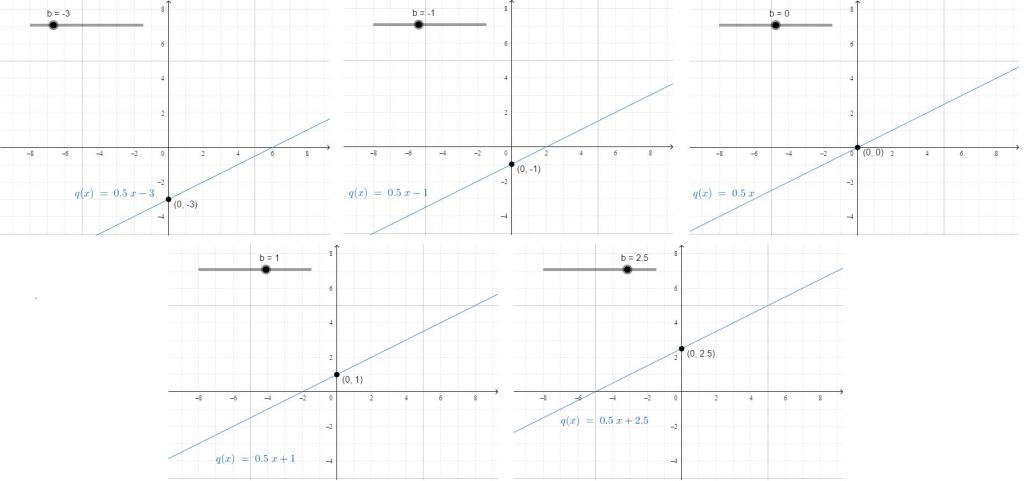
На пример, особа је ходала 10 километара од јутра до 12 сати поподне, а затим је возила бицикл три сата. Онда је удаљеност коју је прекривао за дан: и = 15 × 3 + 10. Ако желите да извучете формулу за израчунавање удаљености на крају сваког сата од три које је јахао на бициклу, можете користити: и = 15к + 10. У један сат дан када је возио 15 × 1 и још 10 прошао, у два је возио 15 × 2, али је свеједно прошао 10.
Граф линеарне функције и = кк + б описује линију која има нагиб к и пресеца ОИ у тачки са координатама (0, б). Анализа једначине често вам омогућава да решите проблеме без прављења графикона. Али да би радили у уму, акције морају бити добро везане за визуелни материјал.
На пример, задатак је да се нађу тачке пресека и = - к 2 и и = 0.5к + 5. Прва функција се смањује, друга се повећава, прва је испод друге, јер су гране параболе доље, а њен врх је на почетку. Линеарна функција би морала имати много већи кут нагиба да би била стрмија и прелазила једну од грана параболе. Према томе, могуће је недвосмислено одредити да нема тачака пресека без конструкције графикона и без прављења супституција.
Посебни случајеви
- Када нема слободног коефицијента, он је (у ствари) једнак нули, што значи да правац сека ОИ на нули.
- Када нема непознатих к или и, и и к су независни један од другог. На пример, и = 5. Без обзира на вредност к, и ће увек бити 5. Графички, ово се може представити као правац паралелан са ОКС.
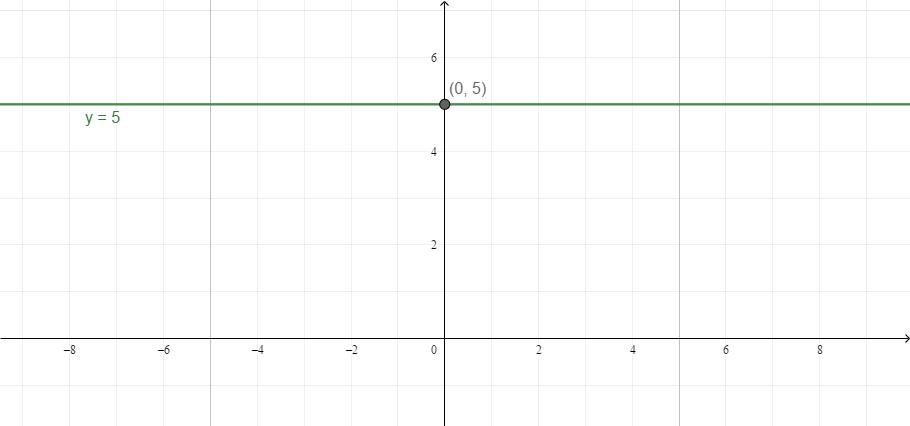
- Исто важи и за случај када је варијабла к једнака броју: варијабла к има константну вриједност.
Анализирајући једнаџбу прије цртања линеарне функције, можете сазнати њезину приближну локацију на ОИ и кут нагиба, а тиме и нагиб. Ово помаже не само да се пронађе права скала и изгради граф, већ и да се реше неки проблеми у уму.