Како пронаћи дужину лука кружнице

Формула за проналажење дужине лука кружнице је прилично једноставна, а врло често на важним испитивањима као што је обједињени државни испит постоје такви проблеми који се не могу ријешити без његове примјене. Потребно је да то знате и за полагање међународних стандардизованих тестова, као што су САТ и други.

Колика је дужина лука кружнице?

Формула је следећа:

л = πр / 180 °

Шта је сваки од елемената формуле:

• л је дужина лука кружнице;
• π је број пи (константна вредност једнака ≈ 3.14);
• р је полупречник датог круга;
• α је вредност угла на којем лежи лук (централно, а не уписано).

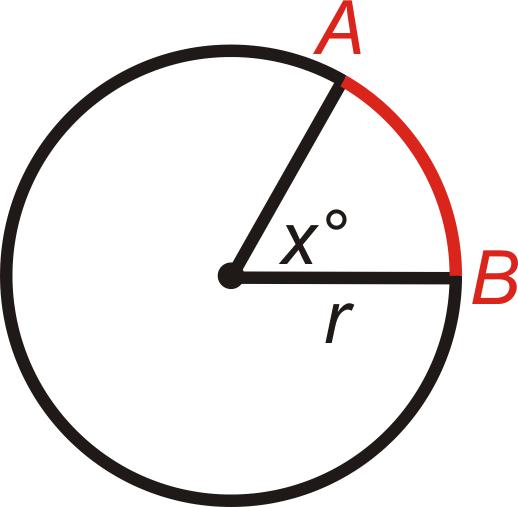
Као што можете видјети, за рјешавање проблема, увјет мора садржавати р и α. Без ове две вредности, дужина лука се не може наћи.

Како је ова формула изведена и зашто изгледа овако?

Све је изузетно лако. Постаће много јасније ако ставите 360 ° у именитељ, и додајте двојку у бројнику испред. Такођер можете а не оставити у дјелићу, повући га и написати знаком множења. Сасвим је могуће приуштити, пошто је овај елемент у нумератору. Тада ће општи приказ бити:

л = (2πр / 360 °) × α

Само због удобности, смањена за 2 и 360 °. А сада, ако пажљиво погледате, можете приметити веома познату формулу за дужину читавог круга, наиме, 2πр. Цијели круг се састоји од 360 °, јер мјеру добијамо на 360 дијелова. Затим се помножимо са бројем α, тј. Са бројем "комада торте" који нам је потребан. Али сви сигурно знају да се број (дакле, дужина читавог круга) не може поделити по степенима. Шта учинити у овом случају? Обично се, по правилу, степен редукује са степеном централног угла, тј. Са α. Уосталом, остају само бројеви, а резултат је коначан одговор.

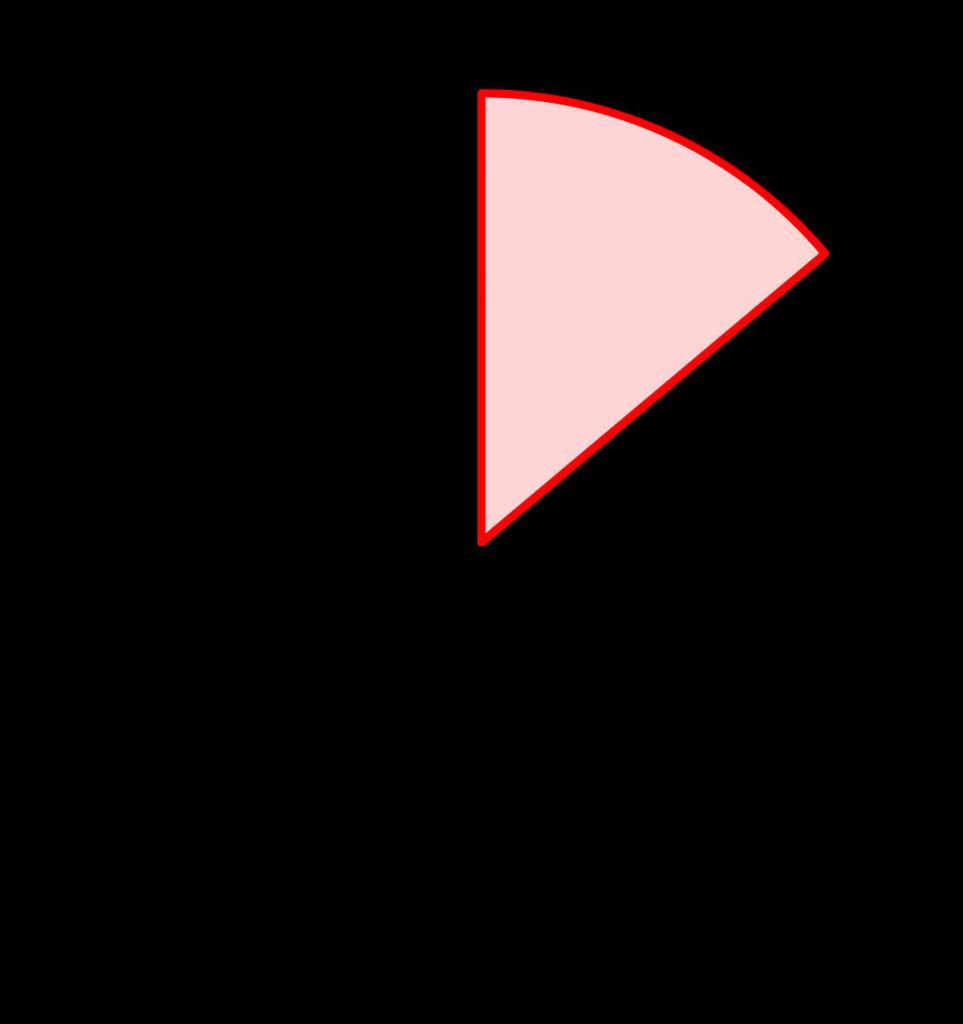
Ово може објаснити зашто је дужина лука кружнице на овај начин и има овај облик.

Пример проблема просечне сложености користећи ову формулу

Услов: Постоји круг полупречника од 10 центиметара. Мерење степена централног угла је 90 °. Нађите дужину лука кружнице формиране овим углом.

Решение: л = 10π × 90 ° / 180 ° = 10π × 1/2 = 5π

Одговор: л = 5π

Такође је могуће да би се уместо степенске мере дала радијанска кута. Ни у ком случају не бојте се, јер је овај пут задатак постао много лакши. Да бисте радиан претворили у степенску меру, требате множити овај број за 180 ° / π. Дакле, сада можете заменити следећу комбинацију уместо α : м × 180 ° / π. Где је м радијанска вредност. Затим се смањује број 180 и број π и добија се потпуно поједностављена формула, која изгледа овако:

л = мр,

где:

• л је дужина лука кружнице;
• м је радијанска мера угла;
• р је полупречник задате кружнице.