Преглед различитих врста призми. Својства троугластих призми

Призма је једна од познатих фигура у простору, чија су својства детаљно проучавана у школском току геометрије. Овај чланак представља преглед различитих врста призми и њихових карактеристика. Карактеристике триангуларне призме су детаљније описане.

Шта је призма?

У чланку почињемо са дефиницијом призме у геометрији. Испод њега, фигура треба да буде формирана од две идентичне паралелне стране, које су равне н-гонс, и н страна паралелограма. Сваки облик који задовољава снимљену дефиницију биће призма.

Изградња призме помоћу геометријских операција није тешка. Потребно је само узети апсолутно било који н-гон и пребацити га паралелно себи за одређени сегмент у простору.

Пошто се ради о полиедру (који се састоји од полигоналних лица), он се не може геометријски добити ротацијом, као што је могуће за цилиндар или конус.

Свака призма има двије основе, које су представљене једнаким н-гонима и н паралелограма (понекад могу бити правокутници, квадрати или ромбови), чија укупност чини бочну површину фигуре. Такође, лик је карактерисан 2 * н једнаким вертикама и 3 * н ивицама, где је н број страна (врхова) полигоналне базе.

Како су призме класификоване?

Број различитих призми је бесконачан. Сви они се међусобно разликују по облику и линеарним димензијама, међутим, постоје само двије карактеристике њихове геометријске структуре, које су основа модерне класификације класе дотичних фигура. Ове карактеристике су следеће:

• основни полигон;
• углови између страна и база.

На изглед призме не утичу други параметри који нису наведени. Обе карактеристике заједно доводе до поделе целе класе на четири типа или типова фигура:

• конвексни и конкавни;
• трокутасто, ..., н-угљеник;
• равна и нагнута;
• исправно и погрешно.

Размотримо детаљније сваку од ових врста призми, чија су својства јединствено одређена горњом класификацијом.

Конвексне и конкавне фигуре

Многи заборављају ову класификацијску ставку када карактеризирају призме, јер у свим геометријским проблемима, по правилу, појављују се истакнуте личности. Тако се назива конвексна призма, која у основи има конвексни полигон. Према томе, ако је полигон конкаван, призма ће такође бити конкавна.

Даље, у тексту ће бити приказане само конвексне призме, али овде ћемо показати, на пример, како изгледа конкавна призма у облику звезде.

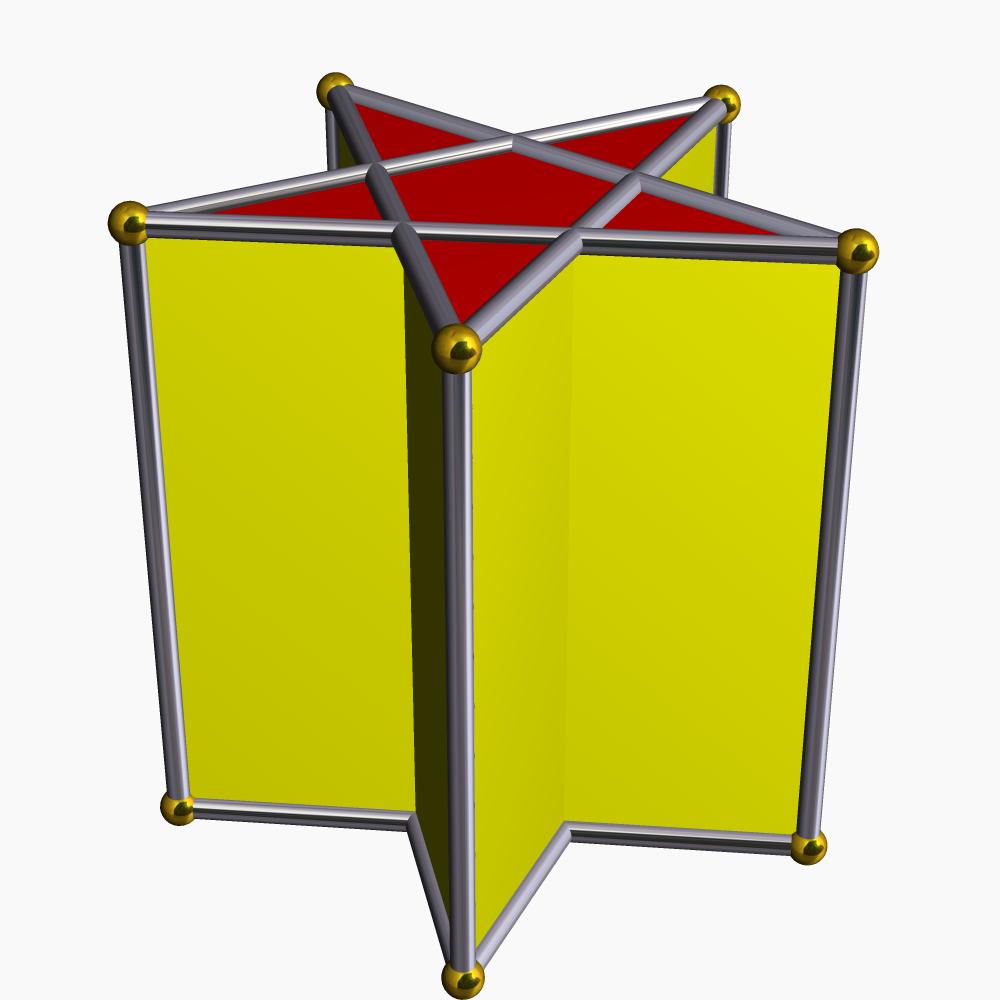
Треба приметити да конкавна призма са минималним бројем страна на бази има четвороугаони облик, док је за конвексну призму она троугластог облика.

Полигоналне призме

Можда је то најпознатија врста класификације призми. Троугласти, четвороугласти, петерокутни, и тако даље, призме ће се звати фигуре које имају одговарајући полигон у бази. На примјер, слика приказује 6 различитих призми - од трокутастог до осмерокутног.

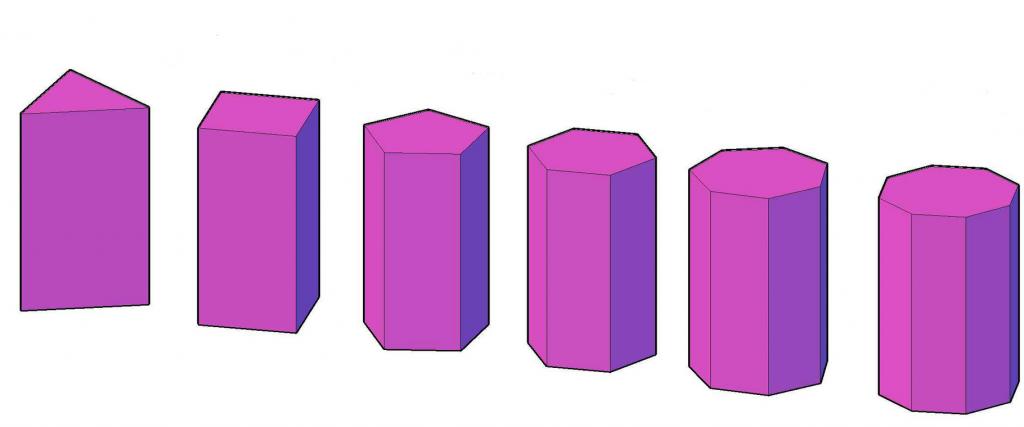
Од свих врста полигоналних призми, само четверокут има своје име - паралелопипед. Ово последње, са одређеним линеарним и угаоним параметрима, може постати коцка.

Косе и равне фигуре

Класификација косих и директних призми заснива се на двослојним угловима између страна фигуре и њене базе. Ако су сви ти диедерни углови једнаки 90 ^о , онда ће се призма назвати равном или правоугаоном. Ако најмање један диелдарни угао није исправан, онда се та фигура сматра нагнутом или косом. Подсјетимо се да говоримо само о дихедрал кутовима између базе и страна. Кутови између две стране се не узимају у обзир.

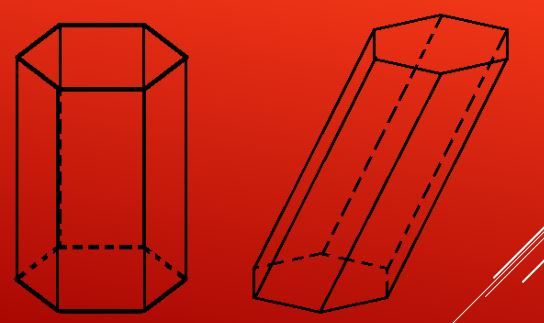
Ово показује како изгледају нагнуте и равне шестерокутне призме. Слика показује да су стране призме правоугаоници (квадрати). Различити типови директних призми и коси могу се добити променом броја страна полигона у њиховим базама.

Право и погрешно

Једноставно речено, ако је призма равна и њена база је н-гон исправна, онда ће она такође бити тачна. Све остале призме које не задовољавају описане услове су нетачне.

Горња слика, која приказује шест полигоналних призми, показује правилне облике.

Погодно је проучавати својства регуларних призми, јер за сваку од њих постоје специфичне формуле за одређивање њихове висине, површине, запремине, дијагоналне дужине и других карактеристика.

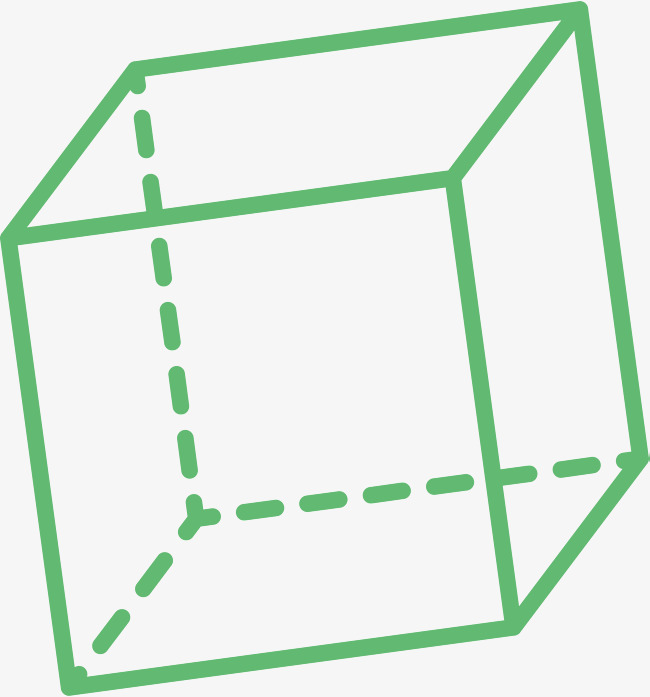
Правилна четверокутна призма чија је висина једнака страни своје базе назива се коцка.

Триангуларне призме

Да се ​​задржимо на троугластим призмама, јер су оне најједноставније међу класама фигура које се разматрају.

Сваки такав облик има 5 лица, 6 једнаких врхова и 9 рубова. Обим троугластих призми се израчунава помоћу формуле која важи за све призме. Изгледа као:

В = С _о * х.

Запремина је једнака производу површине једне базе и висине фигуре. У случају регуларне призме са страном а троугла, ова формула добија облик:

В = /3 / 4 * а ² * х.

С обзиром на питање типова призми, површина троугластих призми дефинисана је као збир површина два идентична троугла и три паралелограма. Ако је исправна призма, онда ће следећа формула за површину С бити важећа:

С = /3 / 2 * а ² + 3 * а * х.

При писању овог израза користили смо чињеницу да су у исправној призми све стране једнаке једна другој и да су правоугаоници.