Паралелност авиона: знак, стање

Свако ко је икада студирао или тренутно студира у школи морао је да се суочи са различитим тешкоћама у изучавању дисциплина које су укључене у програм који је развило Министарство образовања.

С којим се тешкоћама треба суочити

Учење језика прати меморисање постојећих граматичких правила и главни изузеци од њих. Физичко васпитање захтева много прорачуна, физичке кондиције и великог стрпљења ученика.

Међутим, немогуће је упоредити било какве потешкоће које се јављају приликом проучавања тачних дисциплина. Алгебра која садржи замршене начине рјешавања елементарних проблема. Физика са богатим низом формула физичких закона. Геометрија и њене секције, које се заснивају на сложеним теоремима и аксиомима.

Пример би били аксиоми који објашњавају теорију паралелизма авиона, која се обавезно мора запамтити, јер су они основа читавог наставног плана и програма у стереометрији. Хајде да покушамо да схватимо како је то лакше и брже могуће.

Паралелне равни по примјерима

Аксиом, који указује на паралелност равнина, гласи: " Свака два нивоа се сматрају паралелним само ако не садрже заједничке тачке ", тј. Не сијеку се међусобно. Да бисмо замислили ову слику детаљније, као елементарни примјер, можемо дати омјер стропа и пода или супротних зидова у згради. Одмах постаје јасно шта се мисли, а такође потврђује чињеницу да се у уобичајеном случају ови авиони никада неће укрстити.

Други примјер је прозорска стаклена јединица, гдје стаклене мреже дјелују као равнине. Они ни под којим околностима неће формирати тачке укрштања. Поред тога, можете додати полице за књиге, Рубикову коцку, где су равни супротне стране, и други елементи свакодневног живота.

Зрачне летелице су означене посебним знаком у облику двије равне линије "||", које јасно илуструју паралелност равнина. Дакле, примјењујући стварне примјере, може се створити јаснија перцепција теме, и, према томе, може се наставити даље према разматрању сложенијих концепата.

Где и како се примењује теорија паралелних равни?

Када студирају геометријски курс у школи, студенти се суочавају са многостраним проблемима, где је често потребно одредити паралелност линија, линија и равни између себе или зависности равни од других. Анализирајући постојеће стање, сваки задатак може бити повезан са четири главне класе стереометрије.

Прва класа обухвата задатке у којима је неопходно одредити паралелност линије и равни међу собом. Његово решење своди се на доказивање теореме истог имена. Да би се то постигло, потребно је утврдити да ли у тој равнини постоји паралелна правац за правац који не припада дотичној равни.

Друга класа задатака обухвата оне у којима је укључена особина паралелизма равни. Користи се за поједностављење процеса доказивања, чиме се значајно скраћује време за проналажење решења.

Следећа класа покрива низ проблема усклађености са директним основним својствима паралелизма равни. Решење проблема четврте класе је да се утврди да ли је услов паралелизма равни Знајући тачно како се доказује одређени проблем, ученицима постаје лакше да навигирају када користе свој постојећи арсенал геометријских аксиома.

Дакле, задаци, чије стање захтева дефинисање и доказивање паралелности равних линија, праве линије и равни или две равни између њих, своди се на исправан избор теореме и решење према постојећем скупу правила.

О паралелизму линије и авиона

Паралелност равне линије и равнине је посебна тема у стереометрији, јер је то основни концепт на којем се заснивају све наредне особине паралелизма геометријских фигура.

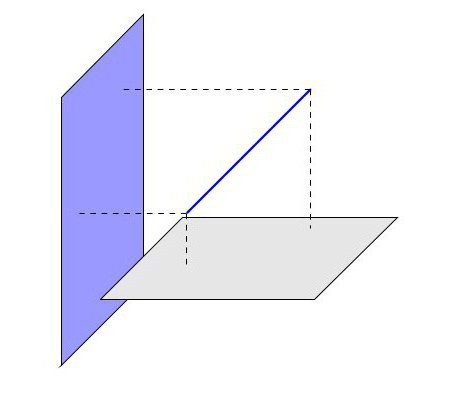
Према постојећим аксиомима, у случају када две тачке равне линије припадају одређеној равни, можемо закључити да у њој лежи и та права линија. У овој ситуацији постаје јасно да постоје три опције за локацију равне линије у односу на равнину у простору:

1. Линија припада авиону.
2. За равну линију и раван постоји једна заједничка точка пресека.
3. За правац и раван, тачке пресека су одсутне.

Посебно смо заинтересовани за ову другу опцију, када нема тачака укрштања. Тек тада можемо рећи да су правац и раван међусобно паралелни. Дакле, потврђује се стање главне теореме о паралелном знаку праве линије и равнине, која каже да: “Ако је правац који не припада дотичној равни паралелан било којој правој линији на овој равни, онда је и правац паралелан са датом равни”.

Потреба да се користи особина паралелизма

Знак паралелности равнина, по правилу, користи се за тражење поједностављеног решења проблема о равнима. Суштина ове особине је следећа: " Ако постоје две линије које се укрштају у једној равни, паралелне са две равне линије које припадају другој равни, онда се такве равни могу назвати паралелне ."

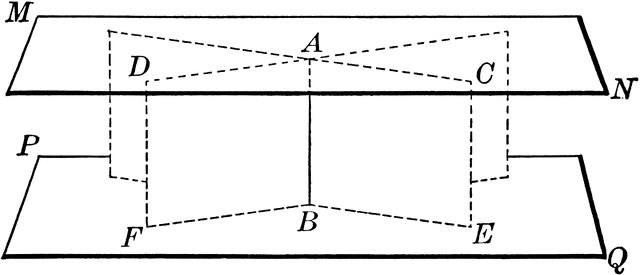
Додатне теореме

Поред употребе знака који доказује паралелност равнина, у пракси се можете сусрести са употребом још две додатне теореме. Први је представљен у сљедећем облику: “ Ако је једна од двије паралелне равнине паралелне с трећом, онда је друга равнина паралелна с трећом или се потпуно поклапа с њом ”.

На основу примењивих теорема, увек се може доказати паралелност равнина у односу на размотрени простор. Друга теорема показује зависност равни на окомитој правој линији и изгледа овако: " Ако су две неусклађене равни окомите у односу на неку равну линију, онда се оне сматрају паралелним једна другој ".

Појам неопходних и довољних услова

При рјешавању проблема доказивања паралелности равнина неколико пута, изведен је нужан и довољан увјет за паралелност равнина. Познато је да је било која равнина дата параметарском једначином форме: А ₁ к + Б ₁ и + Ц ₁ з + Д ₁ = 0. Наше стање се заснива на употреби система једначина које дефинишу распоред равни у простору и представљено је следећим речима: " Да би доказали паралелност две равни, неопходно је и довољно да систем једначина које описују ове равни није компатибилан, тј. Нема решења ."

Основна својства

Међутим, при рјешавању геометријских проблема, кориштење обиљежја паралелизма није увијек довољно. Понекад се јави ситуација када је потребно доказати паралелност двије или више линија у различитим равнинама или једнакост сегмената затворених на тим линијама. Да бисте то урадили, примените својства паралелних равни. У геометрији постоје само два.

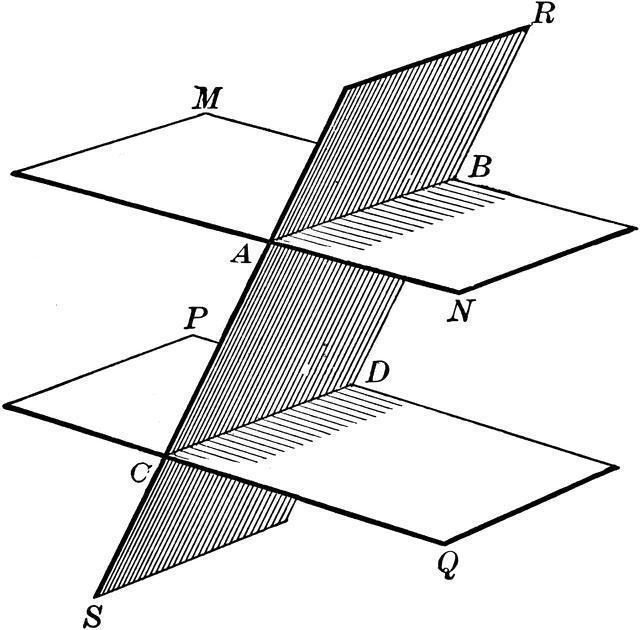
Прво својство нам омогућава да судимо о паралелности линија у одређеним равнима и приказујемо у следећем облику: " Ако две паралелне равни пресеку трећу, онда ће линије које формирају линије пресека такође бити паралелне једна другој ."

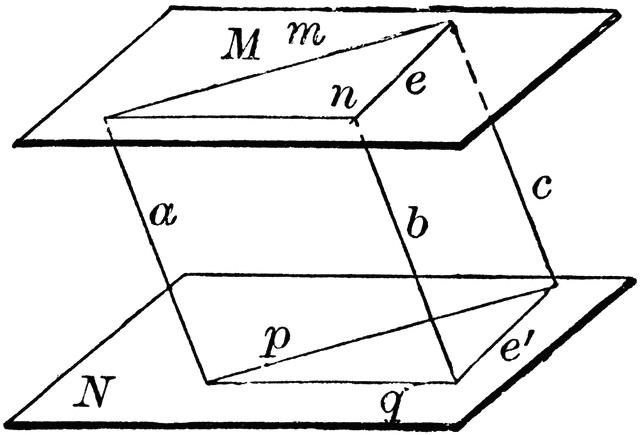
Значење друге особине је да се докаже једнакост сегмената лоцираних на паралелним равним линијама. Његова интерпретација је приказана у наставку. " Ако размотримо две паралелне равни и затворимо регион између њих, онда се може тврдити да ће дужина сегмената које формира ова регија бити иста ."