Вероватноћа догађаја Одређивање вероватноће догађаја

У почетку, пошто је то била само збирка информација и емпиријских опажања игре коцке, теорија вероватноће је постала чврста наука. Први који јој је дао математички оквир су били Фарма и Пасцал.

Од размишљања о вечној теорији вјероватноће

Две личности којима теорија вероватноће дугује многе основне формуле, Блаисе Пасцал и Тхомас Баиес, познате су као дубоко религиозни људи, а други као презбитеријански свештеник. Очигледно, жеља ова два научника да докажу заблуду мишљења о одређеној Фортуне, дајући срећу својим љубимцима, дала је подстицај истраживању у овој области. Уосталом, свака игра на срећу са својим добитком и губицима је само симфонија математичких принципа.

Захваљујући узбуђењу кавалира Мерија, који је био једнако играч и особа која није равнодушна према науци, Пасцал је био присиљен да пронађе начин да израчуна вероватноћу. Де Мере је био заинтересован за такво питање: "Колико пута морате да баците две коцкице у пару да бисте добили 12 бодова више од 50%?" Друго питање, изузетно заинтересовано за господина: "Како поделити опкладу између учесника недовршене игре?" Наравно, Пасцал је успешно одговорио на оба питања де Мере-а, који је постао несвесни покретач развоја теорије вероватноће. Занимљиво је да је персона де Мере остала позната у овој области, а не у литератури.

Претходно, ниједан математичар није покушао да израчуна вероватноћу догађаја, јер се сматрало да је то само одлука о прорицању судбине. Блаисе Пасцал је дао прву дефиницију вјероватноће догађаја и показао да је то специфична фигура која се може математички доказати. Теорија вероватноће је постала основа за статистику и широко се користи у модерној науци.

Шта је несрећа

Ако узмемо у обзир тест који се може поновити бесконачан број пута, онда можемо да дефинишемо случајни догађај. Ово је један од могућих исхода експеримента.

Искуство је спровођење конкретних акција у непромењеним условима.

Да би радили са резултатима искуства, догађаји су обично означени словима А, Б, Ц, Д, Е ...

Вероватноћа случајног догађаја

Да бисмо прешли на математички део вероватноће, потребно је дефинисати све његове компоненте.

Вјероватноћа догађаја је нумерички изражена мјера могућности настанка одређеног догађаја (А или Б) као резултат искуства. Означава вероватноћу као П (А) или П (Б).

У теорији вероватноће, разликује се:

• поуздани догађај се гарантује да ће настати као резултат експеримента П (=) = 1;
• немогуће да се догоди немогућ догађај П (Ø) = 0;
• случајни догађај лежи између поузданог и немогућог, тј. вероватноћа његовог појављивања је могућа, али није загарантована (вероватноћа случајног догађаја је увек унутар 0≤П (А) ≤ 1).

Однос између догађаја

Размотримо и једну и суму догађаја А + Б, када се догађај рачуна у имплементацији најмање једне од компоненти, А или Б, или обоје - А и Б.

У односу једни на друге, догађаји могу бити:

• Екуал то.
• Компатибилан.
• Некомпатибилно.
• Супротно (узајамно искључиво).
• Депендент.

Ако се два догађаја могу појавити са једнаком вероватноћом, онда су они једнако могући .

Ако појава догађаја А не поништи вероватноћу настанка догађаја Б, онда су они компатибилни.

Ако се догађаји А и Б никада не појављују истовремено у истом искуству, они се називају некомпатибилни . Добар пример је бацање новчића: изглед репа је аутоматски не-појављивање орла.

Вјероватноћа за суму таквих некомпатибилних догађаја састоји се од збира вероватноћа сваког догађаја:

Р (А + В) = Р (А) + Р (В)

Ако појава једног догађаја онемогућава да се други догоди, онда се они називају супротним. Тада је један од њих означен као А, а други - А (читај као "не А"). Појава догађаја А значи да се А није појавио. Ова два догађаја формирају комплетну групу са сумом вероватноћа једнаких 1.

Зависни догађаји имају узајамни утицај, смањујући или повећавајући вероватноћу једних за друге.

Однос између догађаја. Примери

Са примерима је много лакше разумети принципе теорије вероватноће и комбинацију догађаја.

Искуство које ће се обавити је да извадите лопте из кутије, а резултат сваког искуства је елементарни исход.

Догађај је један од могућих исхода искуства - црвена лопта, плава кугла, лопта са бројем шест, и тако даље.

Тест број 1. Укључено је 6 лопти, од којих су три у плавој боји, непарни бројеви се примењују на њих, а остала три су црвена са парним бројевима.

Тест број 2. Постоји 6 плавих лопти са бројевима од један до шест.

На основу овог примера, можете позвати комбинације:

• Поуздан догађај. Ин Спанисх Догађај 2 “добијемо плаву куглу” је поуздан, пошто је вероватноћа његовог појављивања 1, јер су све лопте плаве и не може бити пропуста. Док је догађај "добити лопту са бројем 1" - случајан.
• Немогући догађај. Ин Спанисх Но1 са плавим и црвеним лоптицама догађај "гет пурпле балл" је немогућ, јер је вероватноћа његовог појављивања 0.
• Једнаки догађаји. Ин Спанисх Догађаји број 1 „добијају лопту са бројем 2“ и „добијају лопту са бројем 3“ су подједнако могући, а догађаји „добијају лопту са парним бројем“ и „добију лопту са бројем 2“ имају различиту вероватноћу.
• Компатибилни догађаји. Два пута заредом да би добили шест у процесу бацања коцке - то су компатибилни догађаји.
• Некомпатибилни догађаји. У истом исп. Но1 догађаји "добити црвену лопту" и "добити лопту са непарним бројем" не могу се комбиновати у истом искуству.
• Насупротни догађаји. Најживљи пример овога је бацање новчића, када је повлачење орла еквивалентно извлачењу репова, а сума њихових вероватноћа је увек 1 (пуна група).
• Зависни догађаји . Дакле, на шпанском. Бр. 1 се може подесити да извуче црвену куглу два пута за редом. Његова екстракција или не екстракција по први пут утиче на вероватноћу екстракције по други пут.

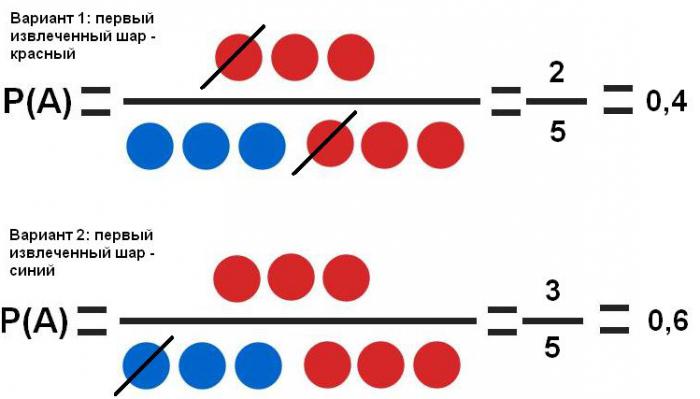
Видљиво је да први догађај значајно утиче на вероватноћу другог (40% и 60%).

Формула вјероватноће догађаја

Прелазак из рефлексије прорицања судбине на тачне податке настаје преношењем теме на математичку раван. То значи да се процјене о случајном догађају као што су "велика вјероватноћа" или "минимална вјероватноћа" могу превести у конкретне нумеричке податке. Такав материјал је већ дозвољен за процену, упоређивање и увођење сложенијих прорачуна.

Са тачке гледишта калкулације, одређивање вероватноће догађаја је однос броја елементарних позитивних резултата и броја свих могућих исхода искуства у односу на одређени догађај. Вероватноћа је означена са П (А), где П значи реч „пробабилит“, која се са француског преводи као „вероватноћа“.

Дакле, формула вероватноће догађаја:

П (А) = м / н,

Где је м број повољних исхода за догађај А, н је збир свих могућих исхода за ово искуство. У овом случају, вероватноћа догађаја увек лежи између 0 и 1:

0 ≤ П (А) ≤ 1.

Израчунавање вероватноће догађаја. Пример

Таке сп. Бр. 1 са лоптама, као што је описано раније: 3 плаве лопте са бројевима 1/3/5 и 3 црвене са бројевима 2/4/6.

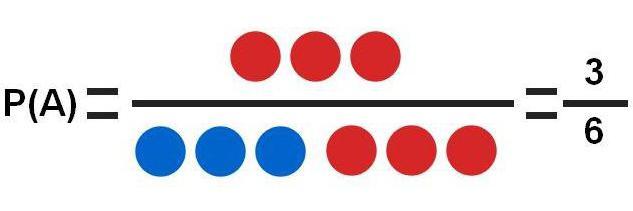
На основу овог теста, може се размотрити неколико различитих задатака:

• А - губитак црвене лопте. Постоје 3 црвене лопте, а укупно има 6 опција.Ово је најједноставнији примјер у којем је вјеројатност догађаја П (А) = 3/6 = 0.5.
• Б - губитак парног броја. Укупан број парних бројева је 3 (2,4,6), а укупан број могућих нумеричких варијанти је 6. Вјероватноћа овог догађаја је П (Б) = 3/6 = 0.5.
• Ц - губитак броја већи од 2. Укупно има 4 такве опције (3,4,5,6) од укупног броја могућих исхода 6. Вјероватноћа догађаја Ц је једнака П (Ц) = 4/6 = 0,67.

Као што се може видети из калкулација, догађај Ц има већу вероватноћу, пошто је број вероватно позитивних исхода већи него у А и Б.

Неусаглашени догађаји

Такви догађаји не могу се истовремено појавити у истом искуству. Као на шпанском Бр. 1 немогуће је истовремено добити плаву и црвену куглу. То јест, можете добити или плаву или црвену куглу. Слично томе, у коцки се чак не може појавити у исто време. непаран број.

Вјероватноћа два догађаја сматра се вјероватноћом њихове суме или производа. Зброј таквих догађаја А + Б се сматра таквим догађајем, који се састоји у појављивању догађаја А или Б, а производ њиховог АБ - у изгледу оба. На пример, појављивање две шестице одједном на лицима две коцкице у једном ролни.

Збир неколико догађаја је догађај који укључује појаву бар једног од њих. Стварање неколико догађаја је заједнички наступ свих њих.

У теорији вероватноће, по правилу, употреба синдиката "и" означава суму, унију "или" - множење. Формуле са примерима ће помоћи да разумемо логику збрајања и множења у теорији вероватноће.

Вероватноћа збира неконзистентних догађаја

Ако се разматра вероватноћа некомпатибилних догађаја, онда је вероватноћа збира догађаја једнака додатку њихових вероватноћа:

Р (А + В) = Р (А) + Р (В)

На пример: израчунајте вероватноћу да је сп. Број 1 са плавим и црвеним куглицама ће испасти број између 1 и 4. Не рачунамо у једној акцији, већ у збиру вероватноћа елементарних компоненти. Дакле, у овом искуству, само 6 лопти или 6 могућих исхода. Бројеви који испуњавају услов су 2 и 3. Вероватноћа одустајања 2 је 1/6, вероватноћа 3 је такође 1/6. Вјероватноћа да број између 1 и 4 падне је једнак:

1/6 + 1/6 = 1/3

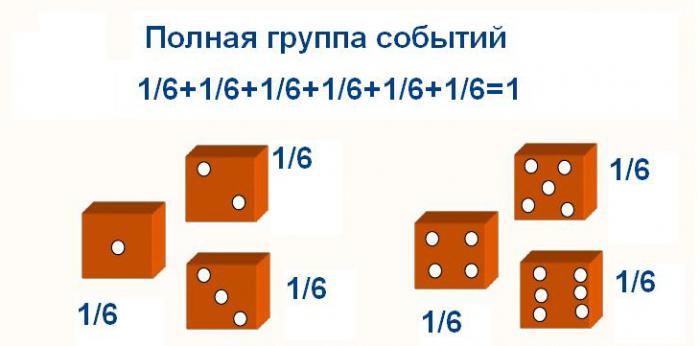
Вјероватноћа збира некомпатибилних догађаја цијеле групе је 1.

Дакле, ако у експерименту са коцком збројимо вероватноће испуштања свих цифара, онда као резултат добијемо једну.

То важи и за супротне догађаје, на пример у искуству са новчићем, где је једна страна догађај А, а други је супротан догађај А, као што је добро познато.

Р (А) + Р (А) = 1

Вероватноћа настанка некомпатибилних догађаја

Множење вероватноћа се користи када се разматра појава два или више некомпатибилних догађаја у једној опсервацији. Вероватноћа да се догађаји А и Б појављују истовремено у њој је једнака производу њихових вероватноћа, или:

Р (А * В) = Р (А) * Р (В)

На пример, вероватноћа да је сп. # 1 као резултат два покушаја два пута плава кугла ће се појавити, једнака

½ * ½ = ¼

То јест, вјероватноћа догађаја, када ће се као резултат два покушаја са извлачењем лоптица само плавих лоптица извадити, износи 25%. Врло је лако направити практичне експерименте за овај задатак и видјети да ли је то заиста случај.

Заједнички догађаји

Догађаји се сматрају заједничким када се појава једног од њих може поклапати са појавом другог. Упркос чињеници да су заједнички, разматра се вероватноћа независних догађаја. На пример, бацање две коцкице може дати резултат када се на њих обадве слике 6. Иако се догађаји поклапају и појављују у исто време, они су независни једни од других - само један шест може пасти, друга кост нема утицаја на њу.

Вјероватноћа заједничких догађаја сматра се вјероватноћом њихове суме.

Вероватноћа збира заједничких догађаја. Пример

Вјероватноћа збира догађаја А и Б, који су међусобно повезани, једнака је збиру вјероватноћа догађаја минус вјероватноћа њиховог рада (тј. Њихова заједничка имплементација):

Р _јоинт. (А + Б) = П (А) + П (Б) - П (АБ)

Претпоставимо да је вероватноћа да погодите мету једном метом 0.4. Тада је догађај А - погодио мету у првом покушају, Б - у другом. Ови догађаји су заједнички, јер је могуће да погодите мету из првог и другог хица. Али догађаји нису зависни. Која је вероватноћа настанка догађаја поразио мету са два хица (најмање један)? Према формули:

0.4 + 0.4-0.4 * 0.4 = 0.64

Одговор на питање је: "Вероватноћа да погодимо мету са два хица је 64%."

Ова формула за вероватноћу догађаја може се применити и на некомпатибилне догађаје, где је вероватноћа заједничког настанка догађаја П (АБ) = 0. То значи да се вероватноћа збира некомпатибилних догађаја може сматрати посебним случајем предложене формуле.

Геометрија вероватноће за јасноћу

Занимљиво је да се вјероватноћа збира заједничких догађаја може представити у облику двије регије А и Б, које се међусобно сијеку. Као што се може видјети на слици, подручје њихове асоцијације једнако је укупној површини минус подручје њиховог раскрижја. Ово геометријско објашњење чини да је формула на први поглед нелогична и разумљивија. Имајте на уму да геометријска решења нису неуобичајена у теорији вероватноће.

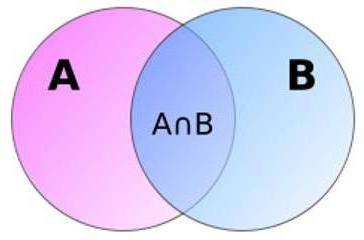
Одређивање вероватноће збира скупа (више од два) заједничких догађаја је прилично гломазно. Да бисте је израчунали, морате користити формуле које су дате за ове случајеве.

Зависни догађаји

Зависни догађаји се позивају ако појава једног (А) од њих утиче на вероватноћу настанка другог (Б). Штавише, узима се у обзир и утицај појављивања догађаја А и његовог не појављивања. Иако се догађаји називају зависним по дефиницији, само један од њих зависи (Б). Уобичајена вероватноћа се означава као П (Б) или вероватноћа независних догађаја. У случају зависних, уводи се нови концепт - условна вероватноћа П _А (Б), која је вероватноћа зависног догађаја Б под условом да се деси догађај А (хипотеза), од чега зависи.

Али, догађај А је такође случајан, па стога има и вероватноћу која мора и може се узети у обзир у извршеним калкулацијама. Следећи пример ће показати како радити са зависним догађајима и хипотезу.

Пример израчунавања вероватноће зависних догађаја

Добар пример за израчунавање зависних догађаја може бити стандардни шпил карата.

Користећи примјер палубе од 36 картица, разматрамо зависне догађаје. Потребно је одредити вероватноћу да ће друга карта, издвојена са палубе, бити од дијамантске одеће, ако је прва карта:

1. Тхе Диамондс
2. Још једно одело.

Очигледно је да вероватноћа другог догађаја Б зависи од првог А. Дакле, ако је прва опција валидна, да је на палуби била 1 карта (35) и 1 дијамант (8) мање, вероватноћа догађаја Б:

П _А (Б) = 8/35 = 0,23

Ако је друга опција валидна, онда је на палуби 35 карата, а пуни број тамбурина (9) је и даље сачуван, затим вероватноћа следећег догађаја Б:

Р _А (В) = 9/35 = 0,26.

Може се видети да ако је догађај А условљен чињеницом да је прва карта тамбура, онда се вероватноћа догађаја Б смањује, и обрнуто.

Множење зависних догађаја

Вођени претходним поглављем, прихватамо први догађај (А) као чињеницу, али ако говоримо у суштини, то је случајно. Вероватноћа овог догађаја, односно вађење дијаманата из шпила карата, једнака је:

П (А) = 9/36 = 1/4

Пошто теорија сама по себи не постоји, већ је намијењена за практичне сврхе, поштено је напоменути да је вјероватноћа да се произведу зависни догађаји најчешће потребни.

Према теореми о производу вероватноћа зависних догађаја, вероватноћа појаве заједнички зависних догађаја А и Б је једнака вероватноћи једног догађаја А помноженог са условном вероватноћом догађаја Б (зависно од А):

П (АБ) = П (А) * П _А (Б)

Онда, у примеру са шпилом, вероватноћа издвајања две карте са дијамантом је:

9/36 * 8/35 = 0.0571, или 5.7%

Вјероватноћа извлачења у почетку није тамбураша, а онда тамбурина, једнака је:

27/36 * 9/35 = 0,19, или 19%

Може се видети да је вероватноћа појаве догађаја Б већа, под условом да се картица из одела, различита од дијаманата, прво екстрахује. Овај резултат је сасвим логичан и разумљив.

Укупна вјероватноћа догађаја

Када проблем са условним вероватноћама постане вишеструк, не може се израчунати коришћењем конвенционалних метода. Када постоји више од двије хипотезе, тј. А1, А2, ..., А _н , .. формира комплетну групу догађаја, под увјетом:

• П (А _и )> 0, и = 1,2, ...
• А _{и ј} А _ј = и, и = ј.
• Σ _к А _к = Ω.

Дакле, формула укупне вероватноће за догађај Б са пуном групом случајних догађаја А1, А2, ..., А _н је једнака _:

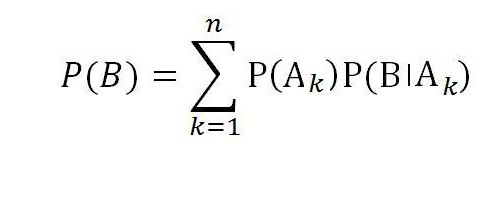
Гледајући у будућност

Вероватноћа случајног догађаја је од суштинског значаја у многим областима науке: економетрији, статистици, физици, итд. Будући да се неки процеси не могу одредити детерминистички, пошто су они сами по себи вјероватноћа, потребни су посебни методи рада. Теорија вероватноће догађаја може се користити у било којој технолошкој области као начин да се утврди могућност грешке или квара.

Можемо рећи да, препознајући вероватноћу, на неки начин правимо теоретски корак у будућност, испитујући га кроз призму формула.