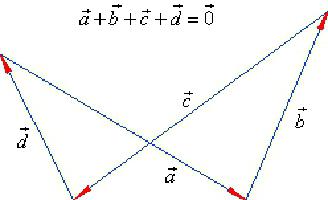
Правила по којима се додају вектори

Како је додавање вектора, студентима није увек јасно. Деца не представљају оно што лежи иза њих. Само морате да запамтите правила, а не да размишљате о суштини. Дакле, ради се о принципима збрајања и одузимања векторских величина за које је потребно пуно знања.

Као резултат додавања два или више вектора, увек се добија један. Штавише, увек ће бити исто без обзира на пријем локације.

Најчешће у школском току геометрије се сматра додавање два вектора. Може се извести правилом троугла или паралелограма. Ове слике изгледају другачије, али резултат акције је један.

Како се додаје правило троугла?

Користи се када вектори нису колинеарни. То јест, не лежи на једној нити на паралелним линијама.

У овом случају, први вектор треба одложити са неке произвољне тачке. Од његовог краја потребно је водити паралелу и једнако другом. Резултат ће бити вектор који почиње од почетка првог и завршава се на крају другог. Слика сличи троуглу. Отуда име правила.

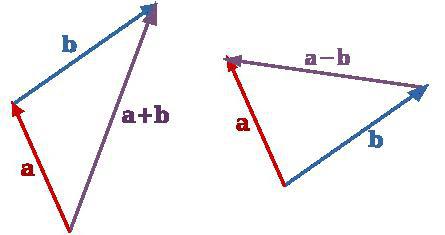
Ако су вектори колинеарни, онда се ово правило може применити. Само цртеж ће бити лоциран дуж једне линије.

Како је додавање према паралелограму правило?

Опет? односи се само на не-колинеарне векторе. Изградња се одвија по другом принципу. Иако је почетак исти. Потребно је одложити први вектор. И од самог почетка - други. На основу њих, попуните паралелограм и нацртајте дијагоналу од почетка оба вектора. Она ће бити резултат. Ово је начин за додавање вектора према правилу паралелограма.

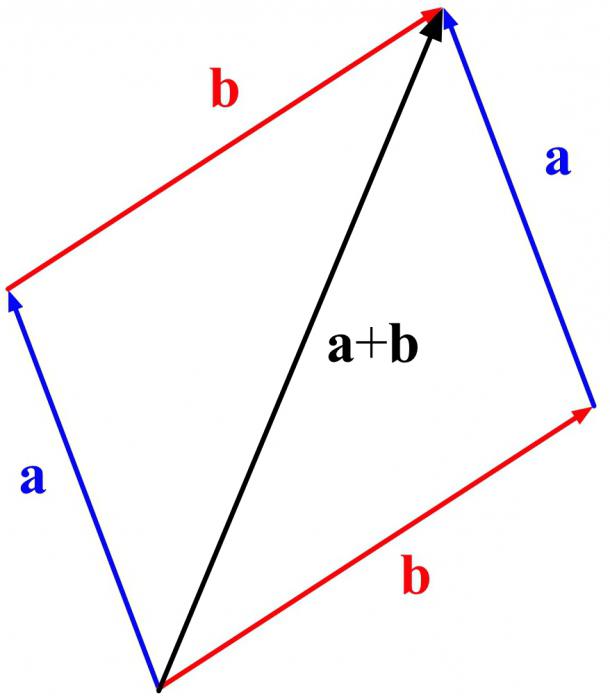
До сада су била два. А шта ако има 3 или 10? Користите следећи трик.

Како и када се примењује правило о полигону?

Ако желите извршити додавање вектора, чији је број већи од два, не треба се плашити. Довољно је да се све то одложи и повеже почетак ланца са његовим крајем. Овај вектор ће бити жељена сума.

Која својства важе за акције са векторима?

О нултом вектору. Који тврди да када се дода, добије се оригинал.

На супротном вектору. То јест, онај који има супротан смер и једнак је величини вредности. Њихова сума ће бити једнака нули.

О комутативности додатка. Оно што је познато још од основне школе. Промена места ставки не мења резултат. Другим речима, без обзира који вектор прво одложио. Одговор ће и даље бити тачан и јединствен.

О асоцијативности додатка. Овај закон вам омогућава да у паровима додате векторе из троструке и да им додате трећу. Ако га напишете уз помоћ знакова, добијате следеће:

први + (други + трећи) = други + (први + трећи) = трећи + (први + други).

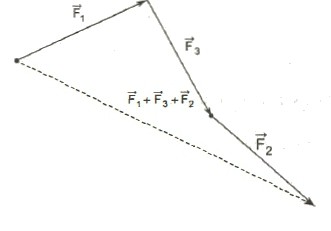
Шта је познато о разлици вектора?

Одвојена операција одузимања не постоји. То је због чињенице да је то заправо додатак. Само други од њих добија супротан смјер. И онда се све ради као да се узима у обзир векторски додатак. Зато практично не говоре о својим разликама.

Да би се поједноставио рад са њиховим одузимањем, правило троугла је модификовано. Сада (када се одузме) други вектор мора бити одложен од почетка првог. Одговор ће бити онај који повезује крајњу тачку дедуктибила са њом. Иако можете одложити како је описано раније, једноставно промјеном смјера другог.

Како пронаћи суму и разлику вектора у координатама?

Проблем даје координате вектора и морате знати њихове вредности за финале. У овој конструкцији није потребно извести. То јест, можете користити једноставне формуле које описују правило додавања вектора. Изгледају овако:

а (к, и, з) + у (к, л, м) = ц (к + к, и + л, з + м);

а (к, и, з) -ц (к, л, м) = ц (кк, ил, зм).

Лако је приметити да координате које треба да додате или одузмете, у зависности од конкретног задатка.

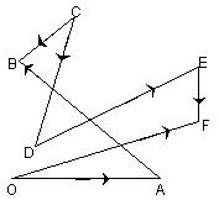
Први пример решења

Цондитион Дати АВСД правоугаоник. Њене стране су 6 и 8 цм, а пресек дијагонала је означен словом О. Потребно је израчунати разлику вектора АО и ВО.

Одлука. Прво морате нацртати ове векторе. Они су усмерени од врхова правоугаоника до тачке пресека дијагонала.

Ако пажљиво погледате цртеж, можете видјети да су вектори већ поравнати тако да је други од њих у контакту с крајем првог. То је само његов правац. Мора почети од ове тачке. То је ако се вектори збрајају, а код проблема - одузимање. Стоп Ова акција значи да морате да додате супротно усмерени вектор. То значи да ВО треба да буде замењен са ОБ. И испоставило се да су два вектора већ формирала пар страна из правила троугла. Дакле, резултат њиховог додавања, односно жељене разлике, је вектор АБ.

И поклапа се са страном правоугаоника. Да бисте снимили нумерички одговор, потребно је следеће. Нацртајте правоугаоник тако да велика страна иде хоризонтално. Нумерисање врхова почиње од доњег левог и иде супротно од казаљке на сату. Тада ће дужина вектора АБ бити једнака 8 цм.

Одговор је. Разлика између АО и ВО је 8 цм.

Други пример и његово детаљно решење

Цондитион Дијагонала ромбова АВСД-а је једнака 12 и 16 цм. Тачка њиховог пресека означена је словом О. Израчунајте дужину вектора формираног разликом вектора АО и ВО.

Одлука. Нека ознака врхова ромба буде иста као у претходном проблему. Слично решењу првог примера, испоставља се да је жељена разлика једнака вектору АБ. Његова дужина је непозната. Решење проблема је смањено да би се израчунала једна од страна ромба.

У ту сврху, морате размотрити троугао АБО. Он је правоугаон, јер се дијагонала ромба секу под углом од 90 степени. Ноге су једнаке половини дијагонала. То је 6 и 8 цм, док се страна у проблему поклапа са хипотенузом у овом троуглу.

Да бисмо је пронашли, треба нам Питагорина теорема. Квадрат хипотенузе ће бити једнак збиру бројева 6 ² и 8 ² . После квадрирања, вредности су 36 и 64. Њихова сума је 100. Из тога следи да је хипотенуза 10 цм.

Одговор је. Разлика између вектора АО и ХЕ је 10 цм.

Трећи пример са детаљним решењем

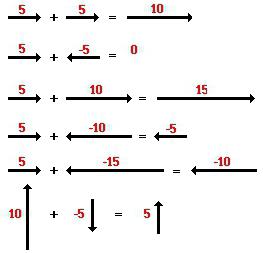
Цондитион Израчунајте разлику и суму два вектора. Њихове координате су познате: у првом - 1 и 2, у другом - 4 и 8.

Одлука. За проналажење износа потребно је у пару додати прву и другу координату. Резултат ће бити бројеви 5 и 10. Одговор ће бити вектор са координатама (5; 10).

За разлику морате извршити одузимање координата. Након извршавања ове акције добијате бројеве -3 и -6. Они ће бити координате жељеног вектора.

Одговор је. Збир вектора је (5; 10), њихова разлика је (-3; -6).

Четврти примјер

Цондитион Дуљина вектора АБ је 6 цм, БЦ - 8 цм, а други је нацртан од краја првог под углом од 90 ступњева. Израчунајте: а) разлику модула вектора БА и БЦ и модула разлике БА и БЦ; б) збира истих модула и модула суме.

Решење: а) Дужине вектора су већ дате у проблему. Стога, израчунавање њихове разлике није тешко. 6 - 8 = -2. Ситуација са модулом разлике је нешто компликованија. Прво морате знати који ће вектор бити резултат одузимања. У ту сврху треба одложити вектор БА, који је усмјерен у супротном смјеру АБ. Затим од свог краја држите вектор сунца, усмеравајући га у правцу супротном од оригинала. Резултат одузимања је вектор ЦА. Његов модул се може израчунати по Питагориној теореми. Једноставне калкулације воде до вредности од 10 цм.

б) Збир модула вектора је 14 цм.За тражење другог одговора, потребна је нека конверзија. Вектор БА је супротно усмерен на онај који даје - АБ. Оба вектора су усмерена из једне тачке. У овој ситуацији можете користити правило паралелограма. Резултат додатка ће бити дијагонала, а не само паралелограм, већ правоугаоник. Његове дијагонале су једнаке, што значи да је модул сума исти као у претходном параграфу.

Одговор: а) -2 и 10 цм; б) 14 и 10 цм.