Тродимензионални простор: вектори, координате

Чак и из школског курса алгебре и геометрије знамо о концепту тродимензионалног простора. Ако разумемо, термин "тродимензионални простор" је дефинисан као координатни систем са три димензије (то сви знају). У ствари, могуће је описати било који предмет волумена помоћу дужине, ширине и висине у класичном смислу. Међутим, хајде, као што кажу, копати мало дубље.

Шта је тродимензионални простор

Како је већ постало јасно, разумевање тродимензионалног простора и објеката који постоје у њему одређују три главна концепта. Истина, у случају тачке то су тачно три вредности, ау случају правих, закривљених, испрекиданих линија или објеката волумена, одговарајуће координате могу бити веће.

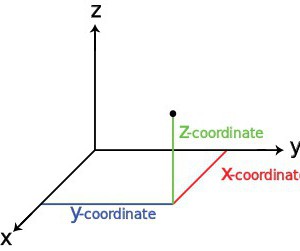
У овом случају све зависи од типа објекта и примењеног координатног система. Данас се картезијански систем, који се понекад назива и правокутни, сматра најчешћим (класичним). О њој и неким другим врстама ће бити речи касније.

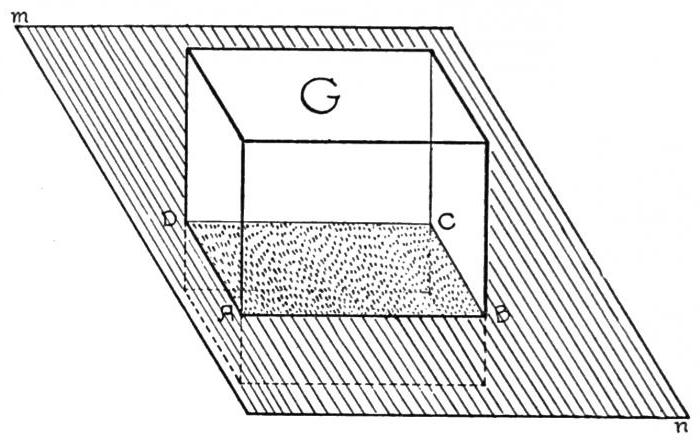
Између осталог, овде је потребно разликовати апстрактне концепте (ако је могуће тако рећи, безобличне) као што су тачке, равне линије или равни и фигуре које имају коначне димензије или чак волумен. За сваку од ових дефиниција постоје и сопствене једначине које описују њихову могућу позицију у тродимензионалном простору. Али сада се не ради о томе.

Појам тачке у тродимензионалном простору

За почетак, дефинишемо шта је тачка у тродимензионалном простору. Уопштено, може се назвати одређеном основном јединицом која дефинише било коју равну или тродимензионалну фигуру, линију, сегмент, вектор, раван итд.

Сама тачка карактерише три главне координате. За њих, у правокутном систему, користе се специјални водичи, названи Кс, И и З осе, прве две осовине које се користе за изражавање хоризонталног положаја објекта, а треће се односи на вертикалну спецификацију координата. Наравно, за погодност изражавања положаја објекта у односу на нулту координату у систему, претпостављају се позитивне и негативне вриједности. Међутим, данас можете пронаћи друге системе.

Врсте координатних система

Као што је већ поменуто, правоугаони координатни систем који је створио Десцартес данас је главни. Ипак, у неким техникама за дефинисање локације објекта у тродимензионалном простору користе се неке друге сорте.

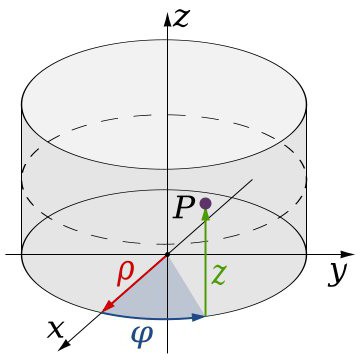
Најпознатији су цилиндрични и сферични системи. Разлика од класичне је у томе што се при одређивању исте три вредности које одређују локацију тачке у тродимензионалном простору, једна од вредности налази у угловима. Другим речима, у таквим системима се користи круг који одговара углу од 360 степени. Одавде и специфичан задатак координата, укључујући елементе као што су радијус, угао и генератрикс. Координате у тродимензионалном простору (систему) овог типа поштују нешто другачије законе. Њихов задатак у овом случају контролише правило десне руке: ако комбинујете палац и кажипрст са Кс и И осе, преостали прсти у савијеној позицији означавају смер З осе.

Концепт линије у тродимензионалном простору

Неколико речи о томе шта чини равну линију у тродимензионалном простору. На основу основног концепта равне линије, ово је нека врста бесконачне линије која се повлачи кроз тачку или две, не рачунајући скуп тачака које се налазе у низу који не мења директан пролаз линије кроз њих.

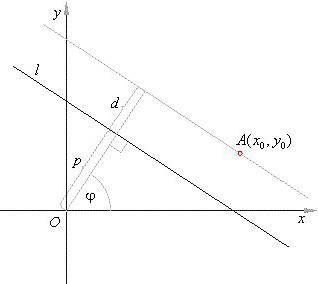
Ако погледате линију која је нацртана кроз две тачке у тродимензионалном простору, мораћете да узмете у обзир три координате обе тачке. Исто важи и за сегменте и векторе. Ово последње одређује основу тродимензионалног простора и његове димензије.

Дефиниција вектора и основа тродимензионалног простора

Као што се обично сматра, у тродимензионалном координатном систему могу постојати три главна вектора који дефинишу основу. Штавише, базе са одговарајућим независним три вектора могу бити безбројне.

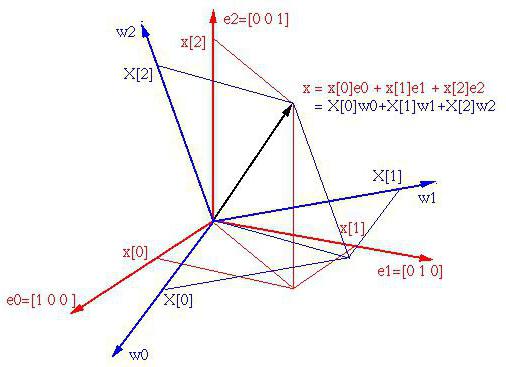
Обратите пажњу на то да могу постојати само три вектора, али овде можете дефинисати онолико колико тројки вектора. Димензија простора одређена је бројем линеарно независних вектора (у нашем случају три). А простор у којем постоји коначан број таквих вектора назива се коначна димензија.

Зависни и независни вектори

Што се тиче дефиниције зависних и независних вектора, вектори који су пројекције (на пример, вектори Кс-осе пројектовани на И-оси) сматрају се линеарно независним.

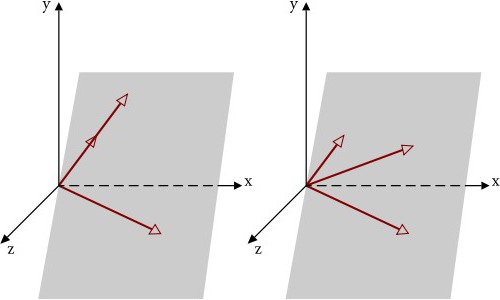
Као што је већ јасно, сваки четврти вектор зависи (теорија линеарних простора). Али три независна вектора у тродимензионалном простору не морају нужно лежати у истој равни. Осим тога, ако дефинишемо независне векторе у тродимензионалном простору, они не могу бити, да тако кажемо, један наставак другог. Као што је већ јасно, у случају када разматрамо три димензије, према опћој теорији, могу се конструисати само три тројке линеарно независних вектора у одређеном координатном систему (без обзира на тип).

Авион у тродимензионалном простору

Ако узмемо у обзир концепт авиона, без улажења у математичке дефиниције, за једноставније разумевање овог појма, такав објекат се може сматрати само дводимензионалним. Другим речима, то је бесконачна збирка тачака где је једна од координата константа (константа).

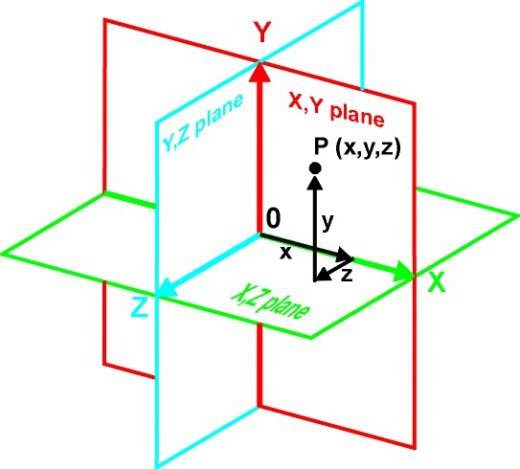
На пример, раван се може назвати било којим бројем тачака са различитим координатама дуж оси Кс и И, али са истим координатама дуж осе З. У сваком случају, једна од тродимензионалних координата остаје непромењена. Међутим, ово је, да тако кажем, општи случај. У неким ситуацијама, тродимензионални простор може да се сијече са равнином дуж свих осе.

Постоји ли више од три димензије

Интересантно је питање колико мјерења може постојати. Сматра се да не живимо у тродимензионалном од класичне тачке гледишта простора, већ у четверодимензионалном. Поред познатих дужина, ширина и висина, овај простор укључује и животни век објекта, а време и простор су веома снажно повезани. Ово је доказао Еинстеин у својој теорији релативности, иако се то више односи на физику него на алгебру и геометрију.

Још једна занимљива чињеница је да су данас научници већ доказали постојање најмање дванаест димензија. Наравно, далеко од свакога ће бити могуће да схвате шта су, јер се односи на одређени апстрактни простор који је изван људске перцепције свијета. Ипак, остаје чињеница. Многи антрополози и историчари тврде да су наши преци могли да имају неке специфично развијене чулне органе попут трећег ока, који су помогли да се сагледа вишедимензионална стварност, а не само тродимензионални простор.

Иначе, данас има доста мишљења о чињеници да је екстрасензорна перцепција такође једна од манифестација перцепције мултидимензионалног света, а може се наћи доста доказа.

Имајте на уму да модерне основне једначине и теореме описују вишедимензионалне просторе који се разликују од нашег четвородимензионалног света, такође није увек могуће. А наука у овој области се више односи на област теорија и претпоставки него на оно што се јасно може осетити или, да тако кажемо, додирнути или видети из прве руке. Ипак, индиректни докази за постојање вишедимензионалних светова, у којима може бити четири или више димензија, данас није сумњиво.

Закључак

Уопштено, врло смо кратко прегледали основне појмове који се односе на тродимензионални простор и основне дефиниције. Наравно, постоји много посебних случајева повезаних са различитим координатним системима. Осим тога, покушали смо да не уђемо у дивљину математике да бисмо објаснили основне појмове, само да би питање које је повезано са њима било разумљиво сваком ученику (да тако кажемо, објашњење је “на прстима”).

Ипак, чини се да се чак и из таквих једноставних интерпретација може закључити да је математички аспект свих компоненти укључен у основни школски курс алгебре и геометрије.