Виетина теорема: примери њене употребе при раду са квадратним једначинама
Приликом проучавања метода рјешавања једнаџби другог реда у школском току алгебре, размотрите својства добивених коријена. Они су тренутно познати као Вјетска теорема. Примери његове употребе дати су у овом чланку.
Куадратиц екуатион
Једначина другог реда је једначина која је приказана на слици испод.
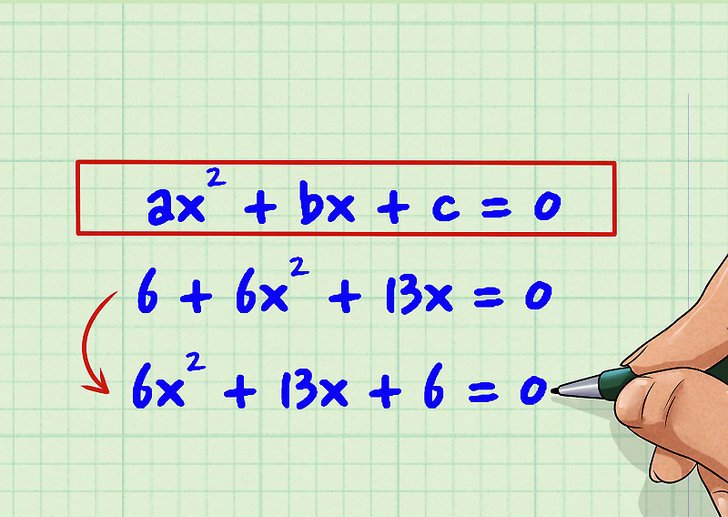
Овде су симболи а, б, ц неки бројеви који се називају коефицијенти дотичне једначине. Да би се решила једнакост, потребно је пронаћи вредности к које чине истину.
Треба имати у виду да је максимална вредност степена у који је Кс подигнут једнак два, онда је и број корена у општем случају једнак два.
Постоји неколико начина за решавање ове врсте једнакости. У овом чланку разматрамо једну од њих, која укључује употребу такозване Виет теореме.
Формулација виетске теореме

Крајем КСВИ., Познати математичар Францоис Виетта (Француз) је, анализирајући својства коријена различитих квадратних једнаџби, напоменуо да одређене комбинације задовољавају одређене односе. Конкретно, ове комбинације су њихов производ и сума.
Виетова теорема успоставља следеће: корени квадратне једначине са њиховом сумом дају однос линеарних и квадратних коефицијената узетих са супротним предзнаком, а када се производе, доводе до односа слободног термина до квадратног коефицијента.
Ако је општа форма једначине написана онако како је приказана на слици у претходном делу чланка, онда се математички ова теорема може написати у облику две једнакости:
- р 2 + р 1 = -б / а;
- р 1 к р 2 = ц / а.
Где је р 1 , р 2 је вредност корена дотичне једначине.
Ове две једначине се могу користити за решавање низа веома различитих математичких проблема. Употреба Виет теореме у примерима са решењем дата је у следећим деловима чланка.
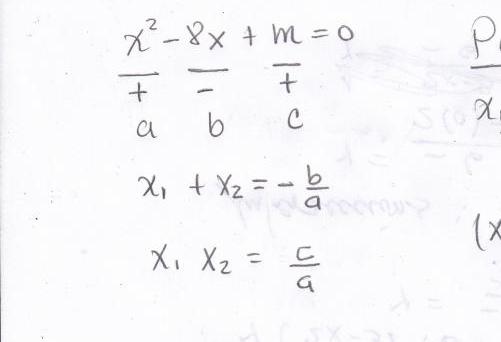
Проблем број 1: враћање једначине
Представљамо следећи проблем о употреби Виет теореме. Пример једначине дат је на следећи начин: -3.4 * к - 3 * с * к 2 + к = 0. Потребно је пронаћи вредности с и к, знајући да су два броја решења ове једначине: -1,2 и 4.
Прво треба да одлучите о вредности коефицијената у овом изразу. Из тога следи да је а = -3 * с, б = -3,4 и ц = к.
Сада можете користити теорему Виета. За суму корена добијамо следећу једнакост: -1.2 + 4 = - (- 3.4) / (-3 * с), одакле добијамо да је с = -0.40476 (препоручује се да се израчуна овај израз помоћу калкулатора). То јест, а = -3 * с = 1.21429. Да би произвели корене имамо:
(-1,2) * 4 = к / 1,21429, одакле је к = -5,82859.
Реконструисана једначина одговара форми: -3.4 * к + 1.21429 * к 2 - 5.82859 = 0. Да би се проверило да ли је проблем исправно решен и да ли је дошло до грешке у његовом решавању, неопходно је заменити познате вредности корена у обновљеном изразу. Добијамо: -3.4 * (-1.2) + 1.21429 * (-1.2) 2 - 5.82859 = 0.00001 ≈ 0 и -3.4 * (4) + 1.21429 * ( 4) 2 - 5.82859 = 0.00005 ≈ 0.
Као што видимо, добијене једнакости су заиста задовољне. Мала грешка је због чињенице да при враћању једнаџбе заокружујемо резултирајуће бројеве на 5 децималних мјеста.
Проблем број 2: пронађите корене једначине
Решење квадратних једначина помоћу Вјетове теореме (види пример испод) могуће је у свим случајевима. То јест, овај метод није универзалан, јер ако се испостави да су коефицијенти једначине "незгодни", онда то неће радити.
Универзалне методе за решавање овог типа изражавања су употреба дискриминантног или додатка на пуни квадрат. Међутим, важност Вјетове теореме у овом случају је да она дозвољава да погодите непознате корене без извођења компликованих математичких прорачуна.
На пример, дат је следећи израз: -к 2 + 2 * к + 3 = 0. Треба да користимо Виетову теорему да пронађемо решења за ову једнакост. Нека његови корени буду бројеви р 1 и р 2 . Тада можете написати следећи систем једнаџби:
р 1 + р 2 = -2 / (- 1) = 2;
р 1 * р 2 = 3 / (-1) = -3.
Сада је потребно погодити која је сума бројева два, а њихов производ ће бити -3. Очигледно, ово су бројеви 3 и -1. Они ће бити корени једначине.
Ако мало пређемо у тему, треба напоменути да се свака једначина другог реда, која се лако представља као производ два фактора, може решити уз помоћ теореме о којој се расправља. Заиста, у овом случају можемо да напишемо (3-к) * (к + 1), ако проширимо заграде, добијемо оригинални израз.
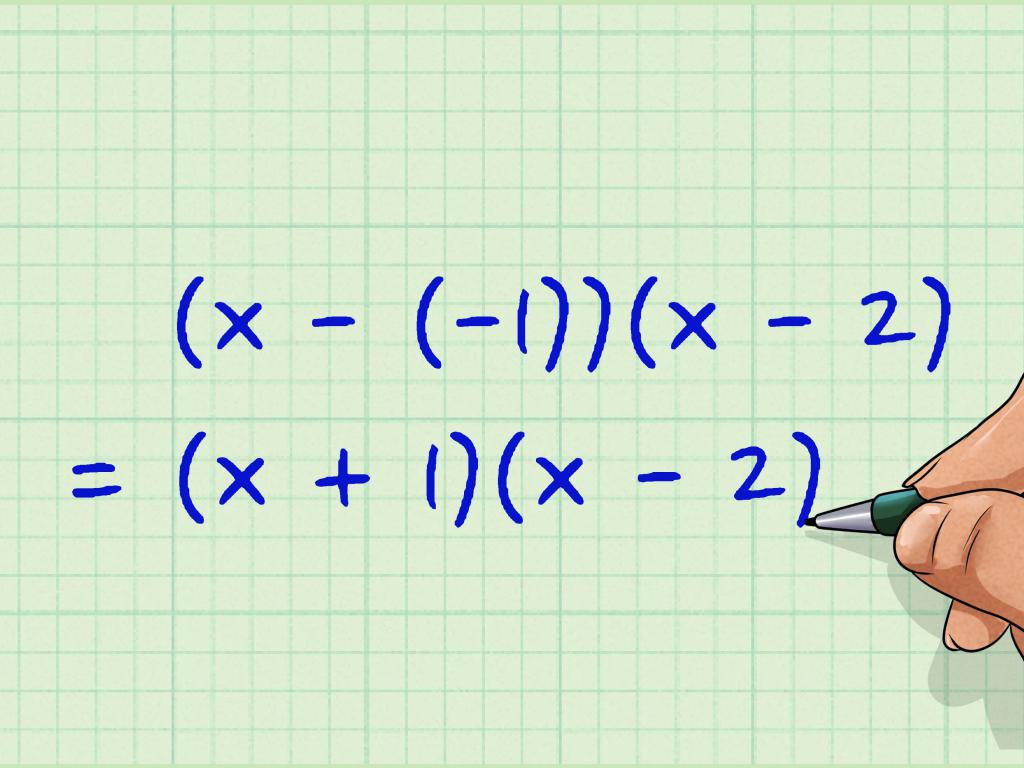
Проблем број 3: збир квадрата
Дајемо још један пример Виет-теореме са решењем. С обзиром на једнаџбу:
6 * к 2 - 13 * к + 11 = 0. Неопходно је пронаћи суму квадрата његових два корена, тј. (Р 1 ) 2 + (р 2 ) 2 .
Наравно, ово решење можете прво решити на један од начина, а затим одговорити на питање проблема. Међутим, ако се присетимо Вјетске теореме и својства квадрата сума, онда нема потребе за тим.
Треба запамтити како се израчунава сума квадрата два броја. Тада налазимо да је за проналажење непознате суме квадрата потребно израчунати вредност израза (р 1 + р 2 ) 2 - 2 * р 1 * р 2 . Користимо обе једнакости разматране теореме, добијамо: (13/6) 2 - 2 * 11/6 = 1.02 (7) (7 у периоду).
Дакле, применом Виетове теореме, уштедели смо време на решавању једначине. Опћенито, својства коријена могу се користити за све задатке који укључују израчунавање њихових различитих комбинација.