Шта су непарни бројеви и како их упознати?

Прије него што говоримо о парним и непарним бројевима, ваља разјаснити неколико тачака о томе које су групе бројева уопће. Ово је неопходно да не бисмо покушали да утврдимо паритет једне фракције.

Који су бројеви за почетак учења у основној школи?

Први су природни. Они су се такође појавили и историјски. Човечанство је требало да броји предмете. Штавише, када се бројање нула не користи, није укључено у групу природних бројева. Овде су сви бројеви већи од један.

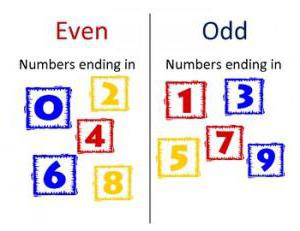
За њих се прво даје дефиниција паритета. Да бисте разумели који је број непаран, морате запамтити знак равног. Завршава се једним од бројева: 0, 2, 4, 6, 8. Сви остали ће бити непарни. Минимум од њих је један. Максимум не постоји.

Који бројеви се настављају?

Вхоле. Њихов скуп већ укључује нула и све негативне бројеве. Ланац природних бројева био је ограничен на лево, а десно се наставио бесконачно. Са целим бројевима испада да је бесконачан број бројева и лево од нуле.

У овом тренутку, дефиниција паритета благо се мења. Сада би га требало подијелити са два без остатка. Дакле, непарни бројеви подељени са два дају одговор са остатком.

Уводи се чак и општи запис: за чак - 2н, непаран - (2н + 1). Ако за природно не постоји само максимална парна или непарна, онда цели бројеви немају минимум.

И шта онда?

Рационални бројеви (друго име - прави). Поред већ поменутих, овај сет укључује и фракције. То су бројеви који се могу представити као два. Први од њих је нумератор и представљен је као цели број. Други је именитељ, који никада није нула.

Иначе, концепт паритета за њих није уведен. Према томе, непарни бројеви написани као фракција уопште не постоје.

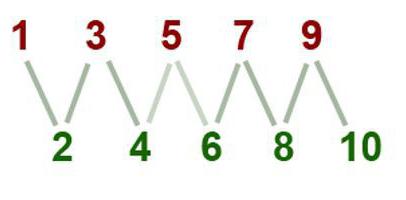
Који резултати дају акције са парним и непарним бројевима?

Они се могу разматрати у циљу повећања сложености аритметичке операције. Тада ће први и други бити збрајање и одузимање. Без обзира на то који је извршен, одговор ће зависити само од почетног пара бројева. На пример, ако су почетни бројеви парни, резултат акције ће бити подељен са два. Исти резултат ће бити ако постоји разлика или збир непарних бројева. Да бисте добили непаран број, морате додати или одузети парни број са непарним бројем.

Ово се може лако проверити коришћењем њиховог општег записа. На пример, додавање два парна броја: 2н + 2н = 4н = 2 * 2н. Овде 2н је паран број, који је још помножен са два. Дакле, дефинитивно ће се потпуно поделити у двојку. То јест, одговор је равномеран.

Када додамо чак и непарном, имамо следећи унос: 2н + (2н + 1) = 4н + 1. Први термин је паран број, коме се додаје. Последњи термин неће дозволити да се овај резултат у потпуности подели на два.

Трећа акција је множење. Када се изврши, увијек ће бити једнаког одговора ако постоји барем један парни фактор. У ситуацији када се два непарна броја множе заједно, резултат ће бити непаран.

Да би илустровали ово друго, потребно је да унесете следећи унос: (2н + 1) * (2н + 1) = 4н + 2н + 2н + 1 = 8н + 1.

Са четвртом акцијом - подела - све није тако јасно. Можете почети са два парна. Прво, може да испадне фракција, онда паритет није питање. Друго, резултат је цео број. Али чак и тада дефинитиван одговор на питање будућег паритета не може се добити. Можете га процијенити тек након подјеле. Одговор може бити и паран и чудан.

Ако је непарни број подељен парним бројем, одговор је увек фракциони. Дакле, његов паритет није одређен.

Када су непарни бројеви укључени у поделу, резултат може бити и фракција. Али ако је одговор потпун, онда ће дефинитивно бити чудно.

При раздвајању чак и непарним, као у претходној ситуацији, постоје двије опције: фракција или цијели број. У другом случају, увек ће бити равномерно.