Шта је гравитација и шта је њено значење за живот на Земљи

Седамнаести век није без разлога назван веком великих астрономских открића. Дугогодишња запажања Галилеја, Коперника, Тиха Брахеа омогућила су Јоханну Кеплеру да формира законе кретања небеских тела. Да би објаснили зашто су планете у бесконачном кретању, оно што их доводи до тога да остану у својој орбити, а шта је гравитација, био је геније - Исак Њутн.

Хипотезе генија

Исак Њутн је формулисао своје законе о кретању не за теорију, већ за практичну примену. Сумирајући податке о вишегодишњим астрономским опажањима и захваљујући законима кретања, овај велики научник је могао да одговори на питање које је збунило више од једне генерације научника: "Шта држи планете у својим орбитама?" магнетне течности. Хвала Невтонов први закон постало је јасно да сила није потребна за равномерно правоцртно кретање. Потребна је сила како би се планете кретале у кривиној орбити. Ако применимо формулу силе из Њутновог другог закона, онда ће она бити једнака продукту убрзања по маси. Невтон је дошао до закључка да убрзање треба да буде једнако в ² / Р. Тако, на пример, лакше небеско тело, Месец ће се окретати око тежег, али му се никада неће приближити. То се може сматрати падом из тангенте у круг на сам круг. У тачки контакта брзина може бити константна или једнака нули, али убрзање је увек присутно. Стално кретање у датој орбити без одсуства видљивог убрзања - ово је Њутнов одговор на питање о кретању планета.

Атракција

Дакле, Месец се креће око Земље, а Земља - око Сунца, покоравајући се одређеној сили. Њутнов гениј се манифестовао у чињеници да је гравитациону силу небеских тела комбиновао са гравитацијом, која је позната сваком становнику Земље. Постоји легенда да је обична јабука која је пала на његову главу гурнута до исправних закључака Њутна. Привлачност јабуке и Месеца на Земљу описана је према апсолутно идентичним законима - закључио је истраживач. Гравитација је добила друго име од речи "гравис", што значи "тежина".

Гравитација

Сумирајући законе кретања планета, Њутн је открио да се снага њихове интеракције може израчунати помоћу формуле: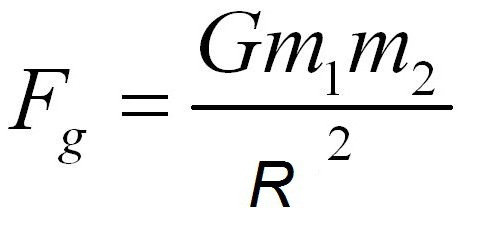

Где су м ₁ м ₂ масе интерактивних тела, Р је растојање између њих, а Г је одређени коефицијент пропорционалности, гравитациона константа. Реч "гравитација" је изабрана апсолутно коректно, јер долази од речи "тежина". Тачан број константе Њутн није био познат, много касније вредност Г успоставила је Кавендиш. Може се видјети да на дјеловање силе привлачења утјечу масе тијела, а удаљеност између њих се узима у обзир. Ниједан други фактор не може утицати на силу гравитације.

Значење закона привлачности

Овај закон је универзалан и може се применити на било која два тела која имају масу. У случају када је маса једног интеракционог тела много већа од масе друге, можемо говорити о посебном случају гравитационе силе, за који постоји посебан термин "гравитација". Овај концепт се користи за проблеме који израчунавају силу гравитације на Земљи или другим небеским телима. Ако заменимо вредност гравитације у формули другог закона Њутна, добијамо вредност Ф = ма. Овде је а убрзање гравитације, што узрокује да тело тежи једни према другима. У задацима везаним за употребу гравитационо убрзање обично се означава словом г. Уз помоћ интегралног рачуна који је развио, Њутн је математички доказао да је сила гравитације у лопти увек концентрисана у центру већег тела. У пару јабука-земља, вектор убрзања је усмерен ка центру земље, у пару земља-сунце је усмерен ка сунцу, и тако даље.

Зависност гравитације од географске ширине

Гравитација на Земљи зависи од висине тела испод површине планете и географске ширине на којој се спроводи експеримент. Висина тела утиче на вредност Р, као што се може видети, што је удаљеност од површине Земље мања, вредност г је мања. Веза гравитације са географском ширином објашњава се чињеницом да је Земља у облику геоида, а не кугле. На половима је мало спљоштен. Дакле, удаљеност од центра Земље до екватора и пола ће бити различита - до 10%. Оваква нескладност чини израчунавање, на примјер, израчуна трансконтиненталних теретних терета, прилично незгодно. Стога се индикатор заснива на сили привлачности на средњим ширинама од 9,81 м / с ² .

Боди веигхт

У свакодневном животу се широко користи таква ствар као што је тјелесна тежина. У физици се означава словом П. Тежина је сила којом тело притиска на ослонац. У домаћем концепту тежине се често замењује појмом "маса", иако су то потпуно различите вредности. У зависности од вредности коју гравитација узима, тежина тела се такође мења. На пример, тежина оловног дела на Земљи и Месецу ће се разликовати. Али маса остаје непромењена и на Земљи и на Месецу. Поред тога, у одређеним случајевима, телесна тежина може бити нула. Тежина је вредност која има правац, а маса је скалар.

Али пошто је, према Њутновом трећем закону, акција једнака опозицији, тежина тела је једнака снази реакције подршке.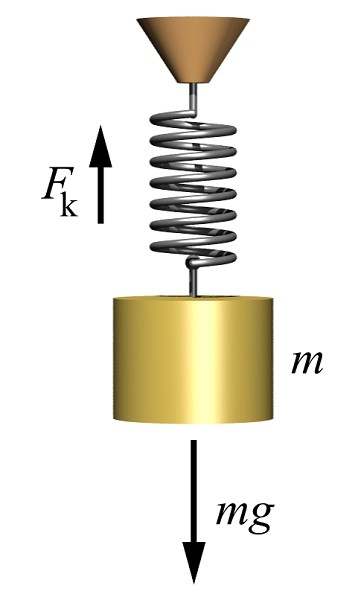

Пошто је сила реакције једноставне подлоге прилично тешка за мјерење, искуство се може "преокренути" обешењем тијела на опругу и мјерењем степена истезања овог прољећа. У овом случају, сила која растеже опругу са оптерећењем имаће потпуно логичан Ф = мг, где је м маса, а г убрзање гравитације.

Оверлоад

Ако се оптерећење са опругом подигне, убрзање гравитације и убрзање лифта ће бити усмерени у супротним правцима. Ово се може представити на следећи начин: Ф = м (г + а). Гравитација, а самим тим и њена тежина, расте.

Да би се повећала тежина која је повезана са додатним убрзањем, постоји посебан термин - преоптерећење. Ефекат преоптерећења доживио је сваки од нас, узимајући лифт или авионом. Космонаути и пилоти суперсоничних авиона доживљавају посебно тешка преоптерећења када скидају свој авион.

Веигхтлесснесс

Када је телу дато убрзање у правцу гравитације, тј. У нашем случају, онда је Ф = м (га). Дакле, телесна тежина постаје мања. У граничном случају, када је а = г и они су усмерени у различитим правцима, може се говорити о нултој тежини, то јест, тело пада константном брзином. Стање у којем је телесна тежина нула назива се бестежинско стање. Особа доживљава стање нулте гравитације у летјелици када се креће са искљученим моторима. Тежина је уобичајена појава за астронауте и пилоте који лете суперсоничним авионима.

Вредност гравитације

Без гравитације, не би било много ствари које нам се чине природним, ствари не би ишле као лавина из планина, не би падала киша, реке не би текле. Земљина атмосфера је очувана гравитацијом. За поређење, планете са мањом масом, као што су Месец или Меркур, врло брзо су изгубиле своју атмосферу и остале су беспомоћне против протока тешког космичког зрачења. Атмосфера Земље одиграла је кључну улогу у настанку живота на Земљи, његовој модификацији и очувању.

Поред гравитације, сила гравитације Месеца делује на Земљу. Захваљујући блиском (на космичком нивоу) суседству на Земљи, постоје осеке и токови, померање континената, и многи биолошки ритмови поклапа се са лунарним календаром.

Према томе, гравитација се не мора посматрати као досадна препрека, већ као користан и неопходан закон природе.