Апсолутно еластичан ударац. Потпуно не-еластични удар

Закони очувања импулса су основни закони природе. Примјер примјене ових закона је феномен судара. Апсолутно еластични и нееластични ударци - промена стања тела као резултат краткотрајне интеракције током њиховог судара.

Механизам интеракције

Најједноставнији тип интеракције физичких тијела је централни судар лопти које имају идеалан геометријски облик. Време контакта ових објеката је у стотинкама секунде.

Према дефиницији, разматра се централни штрајк, у којем линија судара прелази центре лопти. У овом случају, путања интеракције је равна линија која се у тренутку контакта повлачи тачно са елементом контактне површине. У механици се разликују апсолутно еластични и нееластични ударци.

Врсте интеракција

Апсолутно нееластични утицај је примећен код судара два тела пластичних материјала или пластичних и еластичних тела. Након што се заврши, брзина сударајућих објеката постаје иста.

Апсолутно еластичан утицај се уочава у интеракцији предмета од еластичних материјала (на пример, две куглице од тврдог челика или куглице неких врсте пластике и тако даље).

Фазе

Процес еластичног судара се одвија у две фазе:

• Фаза И - тренутак након почетка судара. Силе које дјелују на куглице расту са повећањем напрезања. Повећање напрезања праћено је променом брзине објеката. Тела, чија је брзина била већа, успоравају кретање, а тела убрзавају нижом брзином. Када деформација постане максимална, брзина лопти након апсолутно еластичног удара постаје равнотежа.
• Фаза ИИ. Од момента који карактеризира почетак друге фазе еластичног удара, вриједност деформација се смањује. У овом случају, деформационе силе гурају куглице. Након што деформација нестане, лоптице се уклањају и потпуно обнављају свој првобитни облик и крећу се различитим брзинама. Тако, на крају друге фазе, централни апсолутно еластични утицај трансформише читаву залиху потенцијалне енергије еластично деформисаних тела у кинетичку енергију.

Изоловани системи

У пракси, ниједан ударац није апсолутан (еластичан или нееластичан). Систем у сваком случају комуницира са околном материјом, размењује енергију и информације са околином. Али за теоријска истраживања дозвољено је постојање изолованих система у којима се искључиво интерагују предмети истраживања. На пример, могуће су и апсолутно нееластични и апсолутно еластични удар лопте.

Вањске силе на такав систем не дјелују или се њихов утјецај компензира. У изолованом систему закон конзервације импулса ради у потпуности - сачуван је укупни импулс између сударајућих тела:

М = м _и в _и = цонст.

Овде "м" и "в" је маса одређене честице ("и") изолованог система и његов вектор брзине, респективно.

Да би се сачувала механичка енергија (посебан случај општег закона енергија) постоји потреба да силе које делују у систему буду конзервативне (потенцијалне).

Конзервативне снаге

Конзервативне снаге су оне које не претварају механичку енергију у друге врсте енергије. Ове силе су увек потенцијалне - то јест, рад који такве силе изводе дуж затворене петље је нула. У супротном, силе се називају дисипативни или неконзервативни.

У конзервативним изолованим системима механичка енергија између сударајућих тела такође су сачувани:

В = Вк + Вп = ∑ (мв 2/2) + Вп = цонст.

Овде су Вк и Вп кинетичке (к) и потенцијалне (п) енергије.

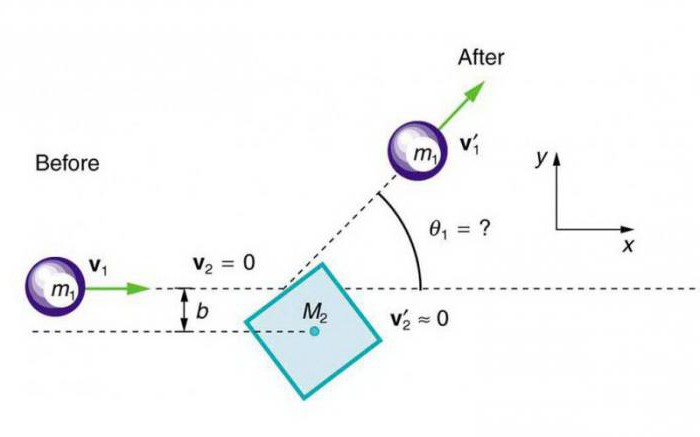
Да бисте проверили релевантност закони о очувању енергије (од горе наведених формула), ако се апсолутно еластична тела ударају под условом да се једна од куглица не помери пре судара (брзина фиксног тела је в ₂ = 0), научници су извели следећу правилност:

м ₁ в ₁ Ки = м ₁ У ₁ + м ₂ У ₂

(м ₁ в ₁ ² ) / 2 × Ке = (м ₁ У ₁ ² ) / 2 + (м ₂ У ₂ ² ) / 2.

Овде м ₁ и м ₂ је маса првог (ударног) и другог (фиксног) кугла. Ки и Ке су коефицијенти који показују колико пута је замах два куглице (Ки) и енергије (Ке) порастао у тренутку када је направљен апсолутно еластичан ударац. в ₁ - брзина ваљања кугле.

Пошто укупни импулс система треба да се очува под било којим условима судара, треба очекивати да ће коефицијент опоравка импулса бити једнак јединици.

Израчунавање силе удара

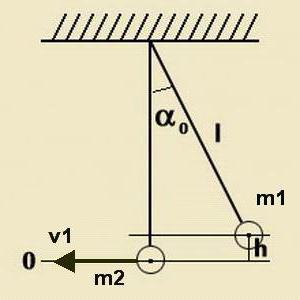
Брзина ударца (отклоњена на кугли) који лети на фиксној (слободно суспендованој) кугли одређена је формулом за закон очувања енергије:

м ₁ гх = (м ₁ в ₁ ² ) / 2

х = л-лцосα = 2лсин ² (α / 2).

Овде је х одступање равни ударне лопте у односу на раван фиксне кугле. л је дужина влакана (апсолутно идентична) на којима су куглице суспендоване. α је угао отклона ударне кугле.

Сходно томе, апсолутно еластичан удар у судару шока (отклоњен на навој) и фиксне (слободно виси на нити) израчунава се по формули:

в ₁ = 2син (α / 2) лгл.

Истраживачки објекат

У пракси се користи једноставна инсталација за израчунавање сила интеракције. Намијењен је проучавању типова удара двају куглица. Инсталација је статив на три вијка који вам омогућују да га поставите хоризонтално. На стативу је централни сталак, на чијем горњем крају су причвршћене посебне суспензије за куглице. Електромагнет је причвршћен за штап, који привлачи и држи, на почетку експеримента, једну од куглица (шок-лопту) у отклоњеном стању.

Величина почетног угла отклона ове кугле (коефицијент α) може се одредити из лучно скалираних дивергентних скала у оба правца. Величина његове закривљености одговара путањи кретања интеракционих лопти.

Процес истраживања

Прво се припрема пар куглица: у зависности од задатка, узимају се еластичне, нееластичне или две различите лоптице. Маса лоптица се уписује у посебну табелу.

Тада је ударни елемент усидрен на електромагнет. На скали одредити кут отклона навоја. Затим се електромагнет искључује, губи своје привлачне особине, а лопта трчи према доље у луку, сударајући са другом, слободном, непомично висећом лоптом, која због импулса (ударца) одступа од одређеног угла. Магнитуда девијације је фиксирана на другој скали.

Апсолутно еластични утицај израчунат на основу експерименталних података. Да би потврдили истинитост закона очувања момента и енергије у случају еластичних и нееластичних судара двају кугли, њихове брзине се одређују прије и након судара. Заснива се на балистичкој методи мерења брзине кретања лоптица према величини њиховог отклона. Ова вредност се мери на скали направљеној у облику кружних лукова.

Значајке прорачуна

При израчунавању утицаја у класичној механици не узимају се у обзир бројни показатељи:

• вријеме судара;
• степен деформације интерактивних објеката;
• хетерогеност материјала;
• брзина деформације (пренос импулса, енергија) унутар лопте.

Сукоб билијарских кугли је добар пример еластичног ударца.