Адијабатски процес, његова суштина и формуле

Адијабатски процес (назван адијабатски у неким изворима) је термодинамички процес који се одвија у одсуству размене топлоте са околином. Постоји неколико фактора који карактеришу ову класу. На пример, адијабатски процес се одвија динамички и поставља се у кратком временском периоду. Постоје процеси ове класе, по правилу, тренутно.

Веза са првим законом термодинамике

Адијабатски процес (адијабатски) може бити директно повезан са први закон термодинамике. Израз „по дефаулту“ гласи: промена количине топлоте у систему током термодинамичког процеса у њој биће нумерички једнака збиру промене унутрашње енергије идеалног гаса и рада тог гаса.

Ако покушамо да пишемо први почетак термодинамике у свом стандардном облику добијамо следећи израз: дК = дУ + дА. Сада ћемо покушати да модификујемо ову формулу у односу на адијабатски процес. Као што је раније поменуто, такви процеси се одвијају под условом одсуства размене топлоте са околином (спољашњим, како то неки књижевни извори називају) медијумом.

У овом случају, формула која описује први закон термодинамике имаће сљедећи облик: дА = -дУ. Сада мало више о модификацији. Ако кажемо да нема измјене топлоте у систему, промена количине топлоте (назначена у формули првог закона термодинамике од стране дК) биће нула. Према томе, један од додатака можемо пренијети с десна на лијево, након чега добијамо формулу редуцирану на раније описану форму.

Последица првог закона термодинамике за адијабатски процес

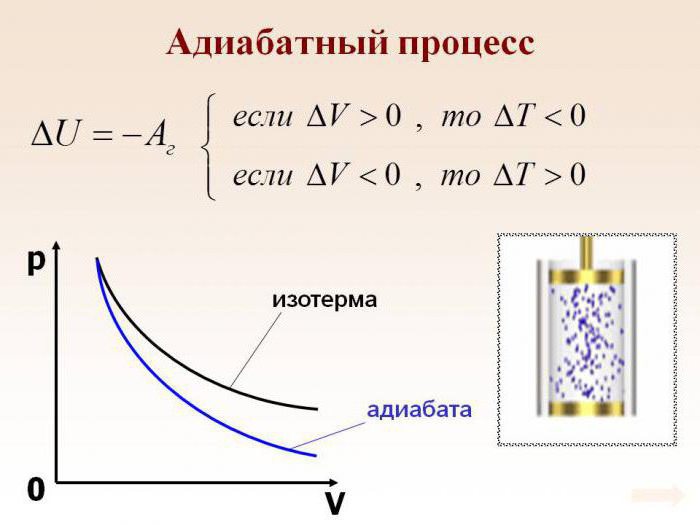
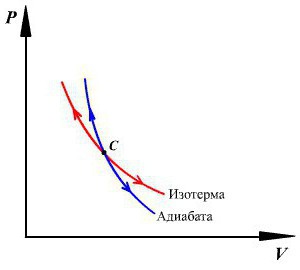
Претпоставимо да је у систему дошло до адијабатског процеса. У овом случају, могуће је, без улажења у најситније детаље, рећи да гас ради свој посао док се шири, али истовремено губи своју унутрашњу енергију. Другим речима, рад који се обавља током адијабатског ширења гаса ће се вршити због губитка унутрашње енергије. Сходно томе, као резултат овог процеса, размотрићемо смањење температуре саме супстанце.

Апсолутно је логично претпоставити да ће, ако је гас адиабатски компримиран, његова температура порасти. Лако је видети да ће се током процеса све главне карактеристике идеалног гаса променити. Ради се о њеном притиску, запремини и температури. Стога је име адијабатског процеса изопроцеса постало груба грешка.

Адијабатски процес. Формуле

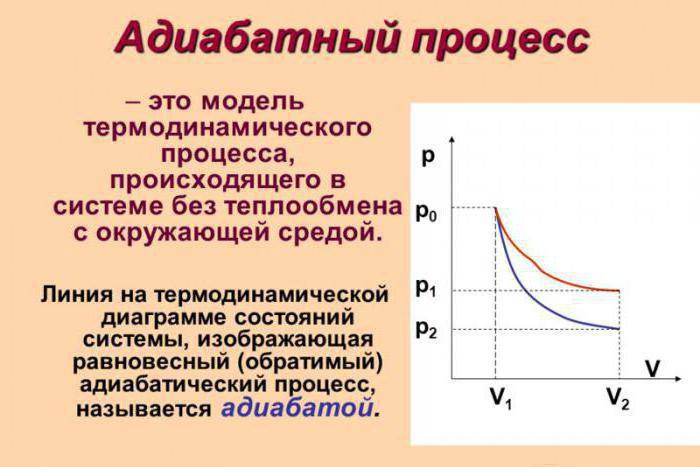
Формула која је изведена из првог закона термодинамике записана је раније. Користећи га, можемо лако да израчунамо рад уопште, који ће гас радити током адијабатског процеса. Као што сте можда претпоставили, ми ћемо то урадити уз помоћ интеграције.

Дакле, да бисмо добили општу формулу за рад за к мола гаса, интегрирамо израз првог закона термодинамике за адијабатски процес. Све ово ће изгледати овако: А = - (интеграл) од дУ. Отворимо овај израз, добијамо: А = - кЦв (интегрални од Т1 до Т2) дТ.

Сада када смо интеграли интеграл у коначни облик, можемо га поједноставити. На излазу добијамо следећу формулу: А = - кЦв (Т2 - Т1). Па, последњи корак ће бити мало поједностављење. Отарасимо се минуса пре формуле. Да бисмо то урадили, направимо малу пермутацију у заградама, мењајући коначну температуру са почетним местима. Као резултат добијамо: А = кЦв (Т1 - Т2).

Адијабатска једначина

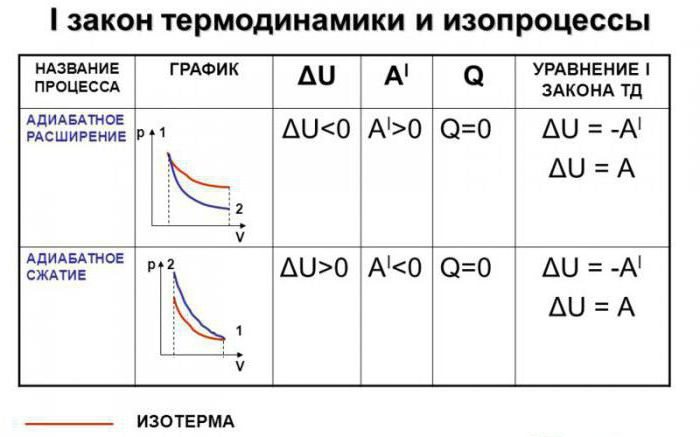
Користећи први закон термодинамике за адијабатски процес, можемо наћи адиабатску једначину. Истовремено ће бити забележен за произвољан број молова идеалног гаса. Дакле, записујемо оригиналну формулу. Изгледа овако: дА + дУ = 0. Али добро знамо да је рад идеалног гаса нумерички ништа више од промене притиска и запремине.

Истовремено се мења унутрашња енергија ће бити једнака раду са супротним предзнаком. И већ смо је пронашли уз помоћ интеграције. Дакле, први закон термодинамике за адијабатски процес може имати следећи облик: пдВ + кЦвдТ = 0. Потребно је искључити један индикатор из ове једначине, наиме, температуру. Уместо тога, његове промене. Да бисмо то урадили, прелазимо на једначину која се често користи у молекуларној физици. Наиме, Мендељејев-Цлапеирон-ова једначина.

Примари екпрессион

Морамо га разликовати, што ћемо и урадити. Дакле, опћенито, једнаџба је сљедећа: ПВ = КСРТ. Због диференцијације, он ће бити сведен на следећи облик: пдВ + Вдп = кРдТ. Одавде можемо изразити промену енергије. Она ће бити једнака левом делу подељеном производу количине супстанце и универзалне гасне константе. Другим речима, формула би била: (пдВ + Вдп) / кР. Остаје само да се поједностави. Као резултат добијемо следећи израз: дТ = (пдВ + Вдп) / к (Цп - Цв)

У ствари, први део задатка је завршен. Остаје само да се све приведе на памет.

Секундарни израз Замена вредности

Узмимо формулу Мендељејев - Цлапеирон добијену као резултат диференцијације и замијенимо је изразом који смо претходно извели за први закон термодинамике с обзиром на адијабатски процес. Па шта ћемо добити? Сви ови незграпни изрази имају следећи облик: пдВ + кЦв ((пдВ + Вдп) / к (Цп-Цв)) = 0.

Да бисмо све ово поједноставили, морамо узети у обзир неколико чињеница. Прво, израз се може поједноставити редуцирањем на заједнички именитељ. Када добијемо једну фракцију, можемо користити добро старо правило, које каже да је фракција нула када је нумератор нула, а именилац је нула. Као резултат комбинације свих ових акција, добијамо следећи израз: пЦпдВ - пЦвдВ + пЦвдВ + ВЦвдп = 0.

Сада је следећи корак подела овог израза на пВЦв. Добијамо суму два дела, дајући као резултат нулу. Ово ће бити Цп / Цв * дВ / В + дп / п = 0. Ова формула мора бити интегрисана. Тада добијамо следећи израз: и (интегрални) дВ / В + (интеграл) дп / п = (интеграл) 0.

Па, онда је све врло једноставно. Користећи формуле интеграција (интегрални табели могу се користити за све што је једноставније), завршавамо са следећим уносом: и лн В + лн п = лн (цонст). Испада да је п (В) и = цонст. У молекуларној физици, овај израз се зове Поиссонова једначина. Многи научни извори ту формулу називају и адијабатском једначином. Истовремено, вредност и, која се јавља у овом запису, назива се адијабатски индекс. Она је једнака (и + 2) / и. Треба напоменути да је адијабатски индекс увек већи од један, што је у принципу логично.

Примери адијабатских процеса

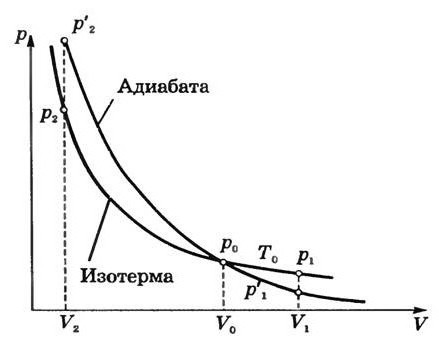
Убрзо након што је откривен адијабатски процес, започео је велики број различитих студија. Тако је створен први теоријски модел који се односи на Царнотов циклус. Она је дозволила успостављање условних ограничења која су ограничавала развој топлотних мотора. Али у случају неких стварних процеса Царнот циклус довољно тешко. Ствар је у томе што се састоји од изотерми. А они, заузврат, захтевају одређену брзину термодинамичких процеса.

Закључак

Да би се заобишли такви проблеми, осмишљен је Отто циклус, као и циклус укапљивање гаса. Постали су широко коришћени у решавању конкретних проблема у пракси. Почетне студије су показале могућност описивања неких природних процеса у адијабатском плану, што нам је омогућило да идентификујемо опште обрасце одговарајућих процеса. Пример адијабатског процеса може се назвати хемијска реакција која се одвија унутар одређене количине гаса, ако је систем затворен и нема размјене топлоте са спољним окружењем.