Основни закони једносмерне струје: дефиниције и формуле
Охмов закон је први пут формулисао немачки физичар и математичар Георг Симон Ом. Охмов закон је основни закон за електрична кола са једносмерном струјом. Она успоставља везу између пада напона или потенцијала, јачине струје и отпора у кругу. Погледајмо ближе Охмов закон и друге основне законе једносмерне струје.
Хисторицал бацкгроунд

Георг Симон Ом је рођен у граду Ерлангену (Немачка) 16. марта 1789. године у протестантској породици. Од раног дјетињства почео је радити у водоводној радионици свога оца. Каријеру физике започела је у Оммеу на Политехничком универзитету у Нирнбергу. До краја дана предавао је физику на Универзитету у Минхену.
Главна заслуга Охма у физици је да је он увео и описао такву физичку величину као електрични отпор. У математичкој форми је прво формулисао везу између потенцијалне разлике, јачине струје и електричног отпора у кругу, за који је јединица отпора названа по његовом презимену.
Охмове нове идеје нису одмах прихваћене од стране свјетске научне заједнице, само 1841. године Краљевско друштво у Лондону додијелило је Оом Цоплеи медаљу, а 1849. Универзитет у Мунцхену му је додијелио Одјел за физику.
Ом током своје научне активности није био ангажован само у електричним круговима. Године 1840. студирао је звучни таласи а од 1852. године бавио се оптиком, нарочито феномен ометања. Научник је умро у Минхену 6. јула 1854. године.
Охмови експерименти
Пре него што је Ом изнео свој чувени закон директна струја други научници су спровели многе експерименте са електричним колима. Треба напоменути експерименте британског Хенрија Цавендисха, који је истраживао понашање Лајденових конзерви 1781. године, али није могао објавити своје закључке.
Физичари данас имају инструменте који омогућавају мерење било којих параметара електричног кола са потребном прецизношћу, а крајем 18. и почетком 19. века није било таквих уређаја, што је ому отежавало да открије закон за једносмерну струју.
Зато је Ом одлучио да направи такав уређај сам. Посебно је користио Цоуломбове торзионе скале, али их је усавршио додавањем магнетног елемента. Истовремено, научник је користио откриће Ханса Цхристиана Оерстета 1819. године о чињеници да проводник са струјом врши силу на магнетизирану иглу у близини њега. Користећи свој нови торзиони баланс, проводне каблове различитих дужина, извор електричне струје и посуде са живом, Охм је био у стању да измери смањење силе са којом проводник са струјом делује на иглу док се дужина тог проводника повећава.
Као резултат ових експеримената, научник је добио следећу математичку зависност: В = 0.41 лг (1 + к), где је В напон у кругу, к је дужина проводника са струјом. Овај израз је касније довео научника до формулације закона једносмерне струје.
Појам јачине електричне струје
Прије разматрања Охмовог закона за истосмјерну струју, уводимо концепт струјне снаге. Неке честице у природи имају такозвани електрични набој. Појам јачине струје директно је повезан са кретањем ових наелектрисаних честица, које су у већини случајева или јони или електрони. Под струјом у физици подразумева се количина пуњења која пролази кроз секцију проводника по јединици времена, која се математички изражава следећим изразом: И = дк / дт.
Јединица јачине струје у СИ је ампер (А), 1 А је јачина струје при којој се пуњење од 1 Ц преноси кроз проводник током 1 с. Пошто се позитивни и негативни набоји крећу у супротним правцима у истом електричном пољу, уобичајено је одредити јачину струје путем правца кретања позитивних набоја.
Брзина кретања набијених честица у електричном пољу

У физици, закон једносмерне струје је формулисан за И = цонст, што значи да свака честица која носи електрични набој мора да се креће константном брзином. Међутим, да би постојала електрична струја, неопходно је имати наелектрисане честице способне за кретање, као и постојање електричног поља. Ово последње делује на електрични набој к са одређеном силом. Ова сила одређена је формулом: Ф = к * Е, овде Е је јакост електричног поља.
Према другом закону Њутна, наелектрисана честица добија убрзање а = к * Е / м, где је м маса честице. Пошто су све вредности у овом изразу константне, убрзање ће такође бити константно и не-нула. Сви ови аргументи су валидни у случају да се наелектрисање креће у празном простору, али ако се креће у било којем медију, онда долази до одређеног отпора из медија.
На пример, електрон који се креће под дејством електричне силе у металном проводнику доживљава константне сударе са јонима који формирају металну кристалну решетку. Ови судари узрокују кретање електрона константном брзином, која се назива брзина кретања. У интеракцији електрона са решеткастим јонима лежи природа електричног отпора.
Кретање електрона у металном проводнику може се упоредити са кретањем капљице кише у ваздуху, јер ова кап не пада са убрзањем слободног пада, већ чини једнолико кретање услед дејства силе отпора из ваздуха.
Локални Охмов закон
У свакој школи почињу да уче законе ДЦ-а у 8. разреду. Истовремено формулише Охмов закон, прво у локалној форми. Да бисте то урадили, узмите, на пример, метални проводник.
У металу, валентни електрони, тј. Електрони смјештени на вањским енергетским љускама атома, слабо су везани за атомске језгре, стога у расутом материјалу не припадају одређеном атомском језгру, већ су слободни или социјализирани. Сваки такав електрон се при собној температури креће ерратично у металном кристалу. Овај покрет је сличан кретању молекула у гасу. Брзина топлинског кретања електрона је велика, износи око 10 6 м / с. Пошто је кретање једнако вероватно у свим правцима, оно не доводи до струје.
Појављује се струја ако је овај водич смјештен у електрично поље. Као резултат тога, електрон добија брзину дрифта, редослед величине 10 −6 м / с. Као резултат тога, електрична струја кроз површину попречног пресека А пише се следећом формулом: И = н * к 2 * Е * т * А / м е , овде н је број електрона који пролазе кроз подручје А у времену т, што је време између два колона електрона са решеткастим јонима, м е - електронска маса
Резултирајући израз се може преписати у облику Ј = И / А = σ * Е, где је Ј густина електричне струје, σ је својство материјала, које се назива електрична проводљивост. Овај израз за густину струје назива се Охмов закон за директну струју у локалној форми.
Охмов закон у макроскопском облику

У школи у 8. разреду, закон директне струје се такође разматра у макроскопској форми. Може се лако добити из релевантног закона у локалној форми. Да би се то постигло, потребно је одредити пад напона или потенцијала у електричном кругу као сљедећи израз: ΔВ = Е * л, гдје је л дужина водича са струјом, а ΔВ напон на његовим крајевима.
Као резултат, Охмов закон ће имати облик: ΔВ = И * л / (σ * А) = Р * И, где је Р електрични отпор. Као што се може видети из закона директне електричне струје у макроскопском облику, вредност Р је инверзна електрична проводљивост σ, то јест, што је материјал боље, мање је електричног отпора. Важно је напоменути и да је σ је својство материјала од којег је направљен проводник, Р је својство одређеног проводника и зависи не само од материјала, већ и од његових геометријских параметара (дужина и површина пресека).
Применљивост и значај класичног Охмовог закона
Охмов закон у класичној или макроскопској форми пише се у облику: В = И * Р. За метале, Р је константна вредност, без обзира на јачину струје која пролази кроз проводник. Међутим, у неким материјалима, као што су полупроводници, то није случај. Материјали у којима је електрични отпор константан називају се линеарни или охмски. За њих је карактеристика струјног напона, тј. Функција напона као функције струје У (И), линеарна.
Охмов закон се не може сматрати основним законом природе, јер важи само за одређену класу материјала, углавном метала. Међутим, она игра важну улогу у физици иу свакодневном животу, јер нам омогућава да на једноставан начин одредимо важне физичке величине у електричном кругу. Конкретно, захваљујући Охмовом закону, ДЦ круг израчунава губитак електричне енергије током преноса и потрошње. Охмов закон се такође користи за израчунавање жељене вредности отпора, који би требало да буде укључен у електрични круг тако да он обавља своје функције уз максималну ефикасност.
Зависност отпорности на температуру за охмске материјале
С обзиром на законитости једносмерних кола, треба напоменути како се отпор мијења с повећањем температуре. По аналогији са електричном проводљивошћу материјала у физици, уводи се појам специфичног електричног отпора ρ, који је повезан са отпором следећом формулом: Р = л * ρ / А.
Емпиријски је утврђено да за охмске материјале ρ покрива следећу температурну зависност: ρ = ρ 0 * [1 + α (ТТ 0 ) + β (ТТ 0 ) 2 + ...], овде ρ 0 је специфична отпорност овог материјала са температура Т 0 , за коју се често претпоставља да је 20 ° Ц.
За металне материјале у опсегу од 0 до 200 ° Ц, отпорност линеарно зависи од температуре, тј. Ρ = ρ 0 * [1 + α (ТТ 0 )], где је α коефицијент температурне отпорности, што је позитивна вредност за метале, сугерише да се електрични отпор повећава линеарно са повећањем температуре за метале. Ово понашање је повезано са смањењем удаљености коју електрон путује између два судара са решеткастим јонима са повећањем температуре.
Интересантно је приметити да се код полупроводника отпор смањује са повећањем температуре. Ова чињеница је повезана са повећањем броја носилаца електричне струје при загревању полупроводничког материјала, на пример, силикона или германијума.
Кирцххоффови закони

У школама у 10. разреду, закони директне струје нису ограничени само на Охмов закон. Школски програм такође проучава законе Кирцххоффа. Постоје два Кирцххоффова закона за истосмјерну струју. На њима се заснива закон о очувању енергије и пуњење у електричном кругу. Следеће су формулације за оба Кирцххоффова закона:
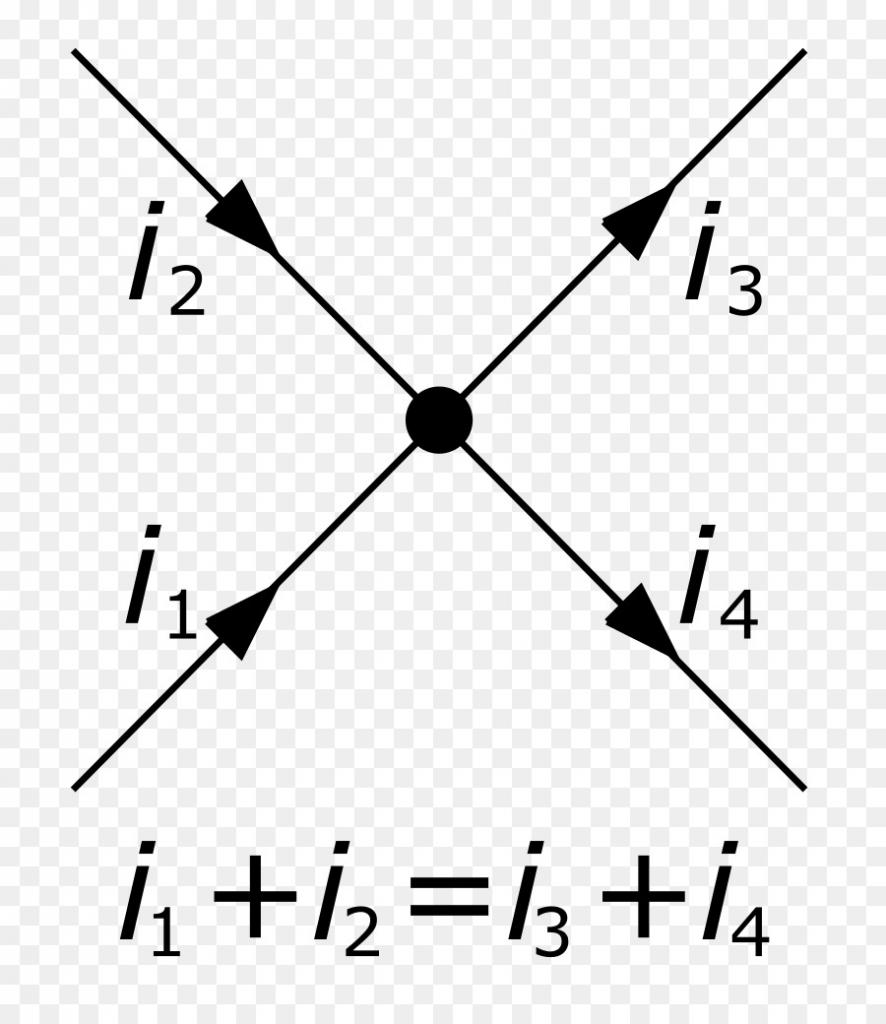
- За сваки чвор електричног кола, сума свих струја које улазе у овај чвор је једнака збиру струја које напуштају. Ова формулација одражава закон очувања набоја.
- У било ком затвореном кругу, зброј свих падова напона на елементима овог круга једнак је напону који му се доводи. Кирцххоффов други закон одражава очување потенцијалне енергије у електричном кругу.
Ови закони су први пут забележени 1846. Тренутно се широко користе у електротехници и електроници за одређивање непознатих струја, напона и отпора у круговима. Треба приметити да у случају присуства нултог електричног отпора у кругу Р, део електричне енергије ће се претворити у топлоту К, која се зове Јоуле и израчунава се по формули К = И 2 Рт, где је т време струје која протиче кроз елемент круга са отпором Р.
Практична примена Охмових и Кирххофових закона
Дајемо пример проблема о законима једносмерне струје. На доњој слици приказан је пример електричног кола, који се састоји од два кола, два извора напона и 5 отпорника са различитим отпорима. Задатак је пронаћи непознате струје И к и И и . Одједном треба рећи да је правац у обе контуре изабран произвољно, у овом случају у смеру казаљке на сату.
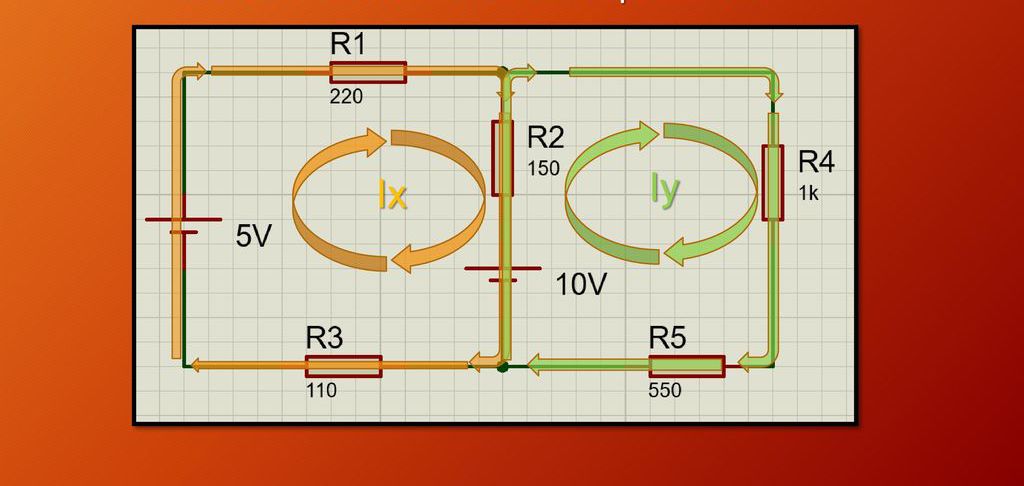
Затим треба да размотрите сваки круг засебно. За почетак, обратите пажњу на коло са непознатом струјом И к . За одабрани круг потребно је примијенити други Кирцххоффов закон, односно закон који каже да напон пада на свим отпорницима и напон напајања из свих извора струје је једнак. Примјењујући овај закон, добијамо: 5-10 = И к * Р 1 + (И к -И и ) * Р 2 + И к * Р3. При састављању овог израза узет је у обзир знак одабраног правца струје И к као позитиван смјер, па је разлика потенцијала на извору 5 В позитивна, а на извору 10 В негативна. Такође, имајте на уму да приликом разматрања овог кола, такође је потребно узети у обзир струју И и која тече према унесеним симболима кроз отпорник Р2.
Сада добијамо сличну једнаџбу за други круг са непознатом струјом И и . Овај израз ће имати облик: 10 = (И и- И к ) * Р 2 + И и * Р 4 + И и * Р 5 . У другом кругу постоји само један извор напајања (10 В), тако да само он улази у израз изведен из 2. Кирцххоффовог закона.
Тако се добијају две једначине у којима постоје две непознанице: И к и И и . Остаје да се ови изрази комбинују у систем линеарних једначина и реше га. На доњој слици приказан је коло у питању и систем једнаџби за одређивање непознатих струја.
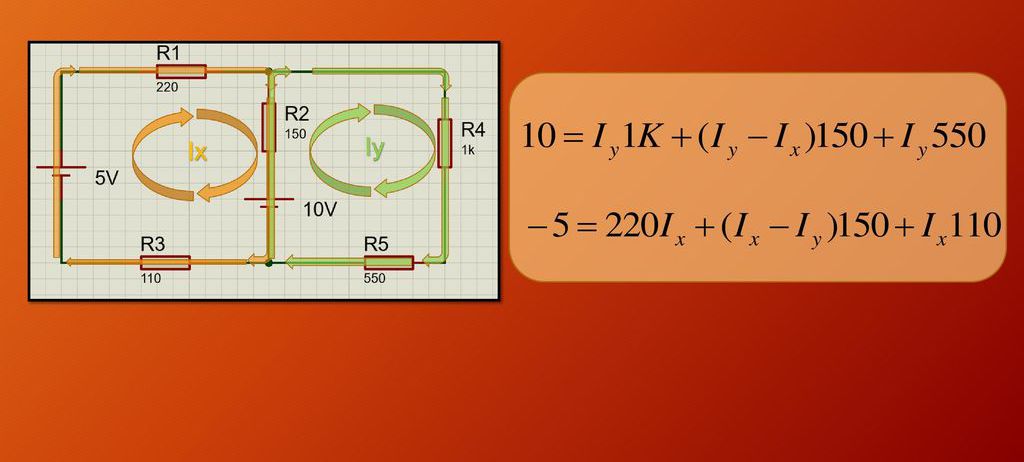
Решавајући систем једначина, добијамо да је И к = -0.00882 А = -8.82 мА, и и и = 0.0051 А = 5.1 мА. Знак минус показује да у стварности струја тече у правцу који је супротан одабраном. Као резултат, струја од 8,82 мА тече кроз отпорнике Р 1 , Р 3 , кроз отпорнике Р4, Р5 - 5,1 мА, а кроз отпорник Р 2 - И и - И к = 13,92 мА.