Комплексни бројеви и акције на њима

Комплексни бројеви , у традиционалном смислу те речи, нису бројеви који се користе у бројању и мерењу, већ математички објекти који су дефинисани доле наведеним својствима.

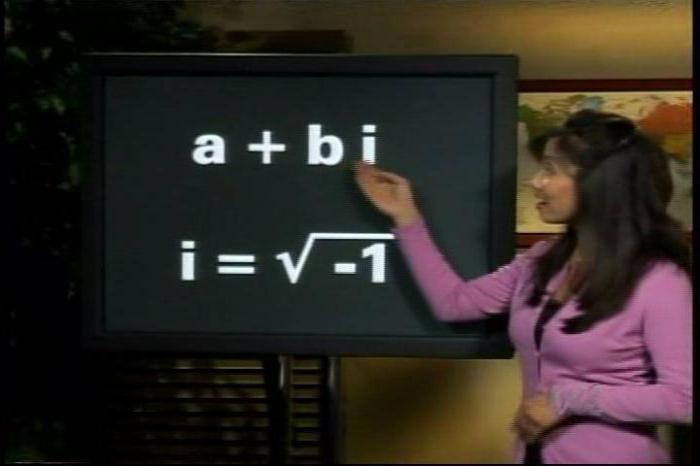
Користите 3 форме комплексног броја: алгебарски, експоненцијални, тригонометријски.

Алгебарски облик

Комплексни бројеви су означени изразом ω + νи, где су ω и ν реални, а симбол и , одређен условом и ² - 1 - јединица је имагинарна.

Према томе, комплексни број ω + νи је подељен на реални и имагинарни део. Ради практичности, она је приказана у једном слову (на пример, η ): η = ω + νи .

Делови комплексног броја η = ω + νи , реални и имагинарни, означени су са ω = Реη, ν = Итη, редом.

Сложени бројеви се сматрају једнаким када су њихови стварни и имагинарни делови еквивалентни. Сматра се да је комплексни број једнак нули ако су његови дијелови, реални и имагинарни, једнаки нули.

Аритметичке операције

Аддитион

Збир комплексних бројева је комплексан број, чији је стварни део еквивалент суми реалних делова, а имагинарни је еквивалент суми имагинарних делова:

η = (ω ₁ + ω ₂ ) + (ν ₁ + ν ₂ ) и.

Речено је да смо међу комплексом η стекли као резултат додавања бројева комплекса :

η = η ₁ + η _2.

Комплекс η ₁ и η _{2 се} називају термини.

Закони о поступку додавања:

1) закон асоцијативности;

2) закон о комутативности .

Комплексно -би-би се назива супротним ω + νи комплексним бројем. Збир супротних комплексних бројева је нула.

Дифференце

Разлика између комплексних бројева назива се комплексни број η једнак зброју броја η ₁ и броја насупрот η ₂ :

η = η ₁ + (- η ₂ ) = (ω ₁ -ω ₂ ) + (ν ₁ -ν ₂ ) и.

За број комплекса η речено је да је стечен одузимањем η ₂ и η ₁ (комплексни бројеви), и записано је:

η = η ₂ -η ₁ .

Ворк

Производ комплексних бројева је комплексан број:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) и.

Речено је да је број комплекса η добијен множењем η ₁ са η ₂ (бројеви η ₁ и η ₂ су сложени), и пишу:

η = η ₁ η ₂ .

Комплекс η ₁ и η _{2 се} називају мултипликатори.

Закони мултиплицирања комплексних бројева:

1) закон асоцијативности ;

2) закон о комутативности .

Дивизија

Посебни комплексни бројеви се називају комплексни η такви да η ₁ = η _1: η ₂ ( η2 0 ) . Приватни комплексни бројеви се израчунавају по формули:

η = (ω ₁ ω ₂ -ν ₁ ν ₂ ) / (ω ² + ν ² ) + (ω ₁ ν ₁ + ω ₂ ν ₁ ) и / (ω ² + ν ² ).

За број η се каже да је добивен дијељењем η ₁ са η ₂ , и написано је:

η = η ₁ / η _{2 .}

Додавање и умножавање комплексних бројева повезано је правилом које се назива закон о дистрибутивној мултипликацији .

Тригонометријски комплексни бројеви

Такође користите други облик снимања комплексних бројева, који се назива тригонометријски.

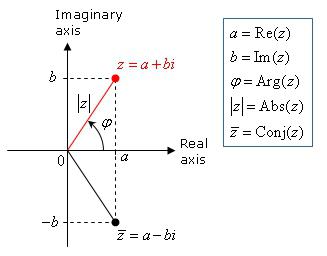
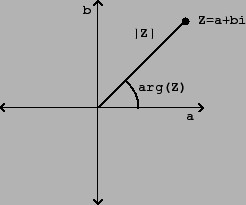
Комплексни број ω + νи се може записати као:

η = к (цосβ + исинβ), где је к ² = ω ² + ν ² .

Овај израз је облик снимања комплексних бројева, који се назива тригонометријски. Модул комплексног броја је реални број к , а угао β , измерен у радијанима, је његов аргумент.

Ако комплексни број није нула, тада је његов модул позитиван; ако је η = 0 , другим речима, ω = ν = 0 , тада је његов модул једнак нули. Модул је дефинисан јединствено.

Продукт тригонометријских комплексних бројева је модул комплексног броја, који је еквивалентан производу фактора, односно њихових модула, а аргумент је еквивалентан суми аргумената фактора:

η ₁ η ₂ = к ₁ к ₂ [цос (β ₁ + β ₂ ) + исин (β ₁ + β ₂ )].

Приватни тригонометријски комплексни бројеви, који нису нула, је комплексан број, чији је модул еквивалентан дјелимичној дивиденди и дјелитељу (њихових модула), а аргумент је еквивалентан разлици аргумената дивиденде и дјелитеља:

η ₁ / η ₂ = к ₁ / к ₂ [цос (β ₁ -β ₂ ) + исин (β ₁ -β ₂ )].

Природни степен броја комплекса

У математици, н-та моћ комплекса η је комплекс в који се јавља као резултат множења η комплекса н пута по себи: в = ηη ... η .

Обично користе краћи унос:

в = η ^н ,

у којој је број η основа степена, а н (природни број) је експонент.

Н-та снага η (комплексни број), која је дата у тригонометријском облику, израчунава се по формули:

η ^н = к ^н (цоснβ + исиннβ).

Ова формула се зове формула Моивре.