Деноминатор геометријске прогресије: формуле и својства
Геометријска прогресија, заједно са аритметиком, важна је нумеричка серија, која се проучава у курсу алгебре у 9. разреду. У овом чланку разматрамо именилац геометријске прогресије и како њена вредност утиче на њена својства.
Дефиниција прогресије геометријског
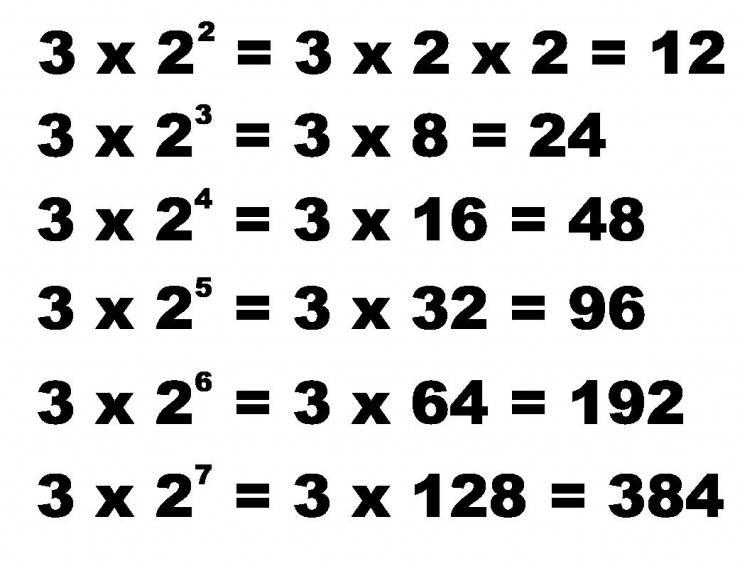
За почетак, дајемо дефиницију овог броја бројева. Геометријска прогресија је серија рационалних бројева која се формира узастопним множењем њеног првог елемента са константним бројем, који се назива именилац.
На пример, бројеви у реду 3, 6, 12, 24, ... су геометријска прогресија, јер ако помножимо 3 (први елемент) са 2, добићемо 6. Ако се 6 множи са 2, добијамо 12, и тако даље.
Чланови предметне секвенце обично су означени са и , где је и цео број који означава број елемента у серији.
Горња дефиниција прогресије се може написати на језику математике на следећи начин: а н = б н-1 * а 1 , где је б именилац. Лако је проверити ову формулу: ако је н = 1, онда б 1-1 = 1, и добијемо 1 = а 1. Ако је н = 2, онда је а н = б * а 1 , и поново долазимо до дефиниције разматраног низа бројева. . Слични аргументи могу се наставити за велике вриједности н.
Деноминатор прогресије геометријског
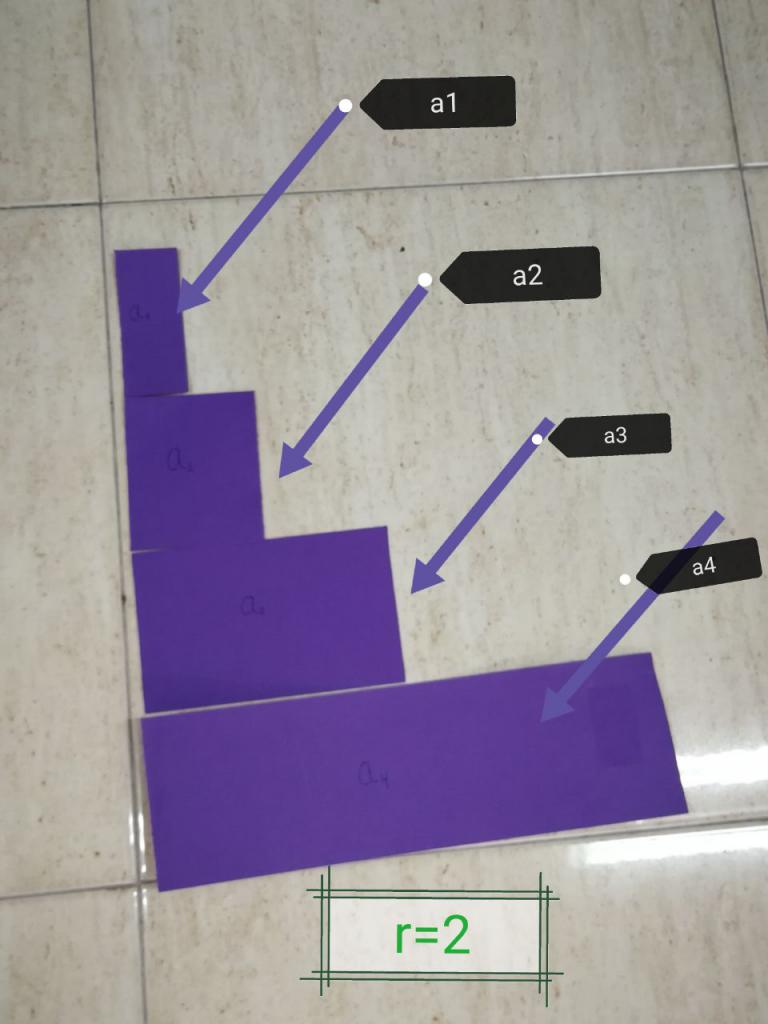
Број б у потпуности одређује природу читавог низа бројева. Деноминатор б може бити позитиван, негативан и такође имати вредност већу од једне или мање. Све ове опције доводе до различитих секвенци:
- б> 1. Постоји све већи број рационалних бројева. На пример, 1, 2, 4, 8, ... Ако је елемент а 1 негативан, онда ће се цео низ повећавати само у апсолутној вредности, али ће се смањивати у односу на знак бројева.
- б <-1. У овом случају, говоримо о варијабилној серији, тј. Сусједни елементи ће се разликовати у знаку. На пример, 1, -2, 4, -8, 16, ...
- -1 <б <1. Ово је посебан случај који има своје име - смањење бесконачне геометријске прогресије. Његова главна карактеристика је да, без обзира на знак деноминатора, тежи ка некој коначној суми када додаје бесконачан број њених елемената.
- б = 1. Такав случај се често не назива прогресијом, јер постоји уобичајена серија идентичних рационалних бројева. На пример, -4, -4, -4.
Формула за суму
Пре него што пређемо на разматрање специфичних задатака користећи називник типа прогресије о којој се ради, треба дати важну формулу за суму њених првих н елемената. Формула има облик: С н = (б н - 1) * а 1 / (б - 1).
Овај израз можете добити сами ако узмете у обзир рекурзивну секвенцу чланова прогресије. Такође имајте на уму да је у горњој формули довољно знати само први елемент и именилац да би се пронашао збир произвољног броја чланова.
Бесконачно смањивање секвенце
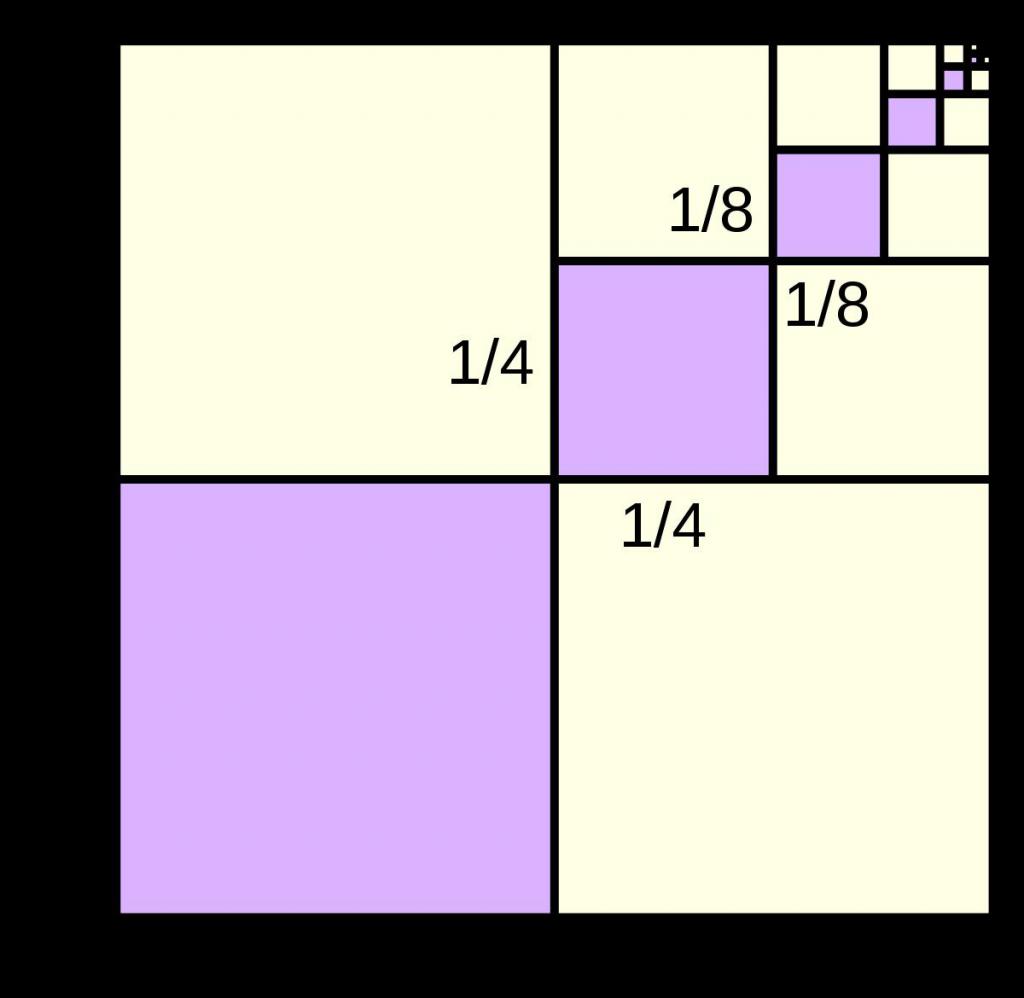
Изнад је објашњено шта је то. Сада, знајући формулу за С н , примените је на ову серију бројева. Будући да било који број чији модул није већи од 1, тежи нули када се подиже на велике степене, тј. Б> => 0, ако је -1 <б <1 (| б | <1), онда се општа формула за суму конвертује у следећи израз: С а = а 1 / (1 - б).
Пошто је разлика (1 - б) увек позитивна, без обзира на вредност имениоца, знак суме опадајуће бесконачне прогресије геометријског С ∞ је јединствено одређен знаком његовог првог елемента а 1 .
Сада ћемо размотрити неколико задатака, гдје ћемо показати како примијенити знање стечено на конкретним бројевима.
Проблем број 1. Израчун непознатих елемената прогресије и износа
Узимајући у обзир напредак геометријског, именитељ прогресије 2, и његов први елемент 3. Који ће бити његови 7. и 10. чланови, а који је збир његових седам почетних елемената?
Стање проблема је довољно једноставно и укључује директну употребу горе наведених формула. Дакле, да бисмо израчунали елемент са бројем н, користимо израз а н = б н-1 * а 1 . За седми елемент имамо: а 7 = б 6 * а 1, замењујући познате податке, добијамо: а 7 = 2 6 * 3 = 192. Настављамо на исти начин за 10. члан: а 10 = 2 9 * 3 = 1536 .
Користимо добро познату формулу за суму и одредимо ову вредност за првих 7 елемената серије. Имамо: С7 = (2 7 - 1) * 3 / (2 - 1) = 381.
Проблем број 2. Одређивање суме произвољних елемената прогресије
Нека је -2 једнако имениоцу прогресије у геометријској прогресији б н-1 * 4, где је н цео број. Потребно је одредити износ од петог до десетог елемента ове серије.
Проблем који се поставља не може се решити директно користећи познате формуле. Може се ријешити са 2 различите методе. За потпуност, дат ћемо обоје.
Метод 1. Његова идеја је једноставна: потребно је израчунати двије одговарајуће количине првих чланова, а затим одузети једна од друге. Израчунамо мању суму: С 10 = ((-2) 10 - 1) * 4 / (-2 - 1) = -1364. Сада израчунавамо велику количину: С 4 = ((-2) 4 - 1) * 4 / (-2 - 1) = -20. Имајте на уму да су у последњем изразу сумирани само 4 термина, јер је 5. већ укључен у суму која се израчунава условом проблема. Коначно, узмите разлику: С510 = С10-С4 = -1364 - (-20) = -1344.
Метод 2. Пре него што замените бројеве и бројите, можете добити формулу за суму између чланова м и н серије која се разматра. Делујемо на исти начин као у методи 1, радећи само прво са симболичком репрезентацијом суме. Имамо: С н м = (б н - 1) * а 1 / (б - 1) - (б м - 1 - 1) * а 1 / (б - 1) = а 1 * (б н - б м - 1 ) / (б - 1). Можете заменити познате бројеве у резултујућем изразу и израчунати коначни резултат: С 10 5 = 4 * ((-2) 10 - (-2) 4 ) / (-2 - 1) = -1344.
Проблем број 3. Шта је именилац?

Нека је а 1 = 2, пронађемо именитељ прогресије геометријског, под условом да је његова бесконачна сума 3, а познато је да је то низ који се смањује.
Стањем проблема није тешко погодити која формула треба користити за њено рјешавање. Наравно, за суму прогресије се бескрајно смањује. Имамо: С а = а 1 / (1 - б). Одакле изражавамо именитељ: б = 1 - а 1 / С ∞ . Остаје да замени познате вредности и добије тражени број: б = 1 - 2/3 = -1 / 3 или -0.333 (3). Могуће је квалитативно проверити овај резултат ако се сјетимо да за ову врсту секвенце модул б не смије ићи даље од 1. Као што се може видјети, | -1 / 3 | <1.
Проблем број 4. Опоравак серије бројева
Нека су дани 2 елемента нумеричког низа, на пример, 5 је 30, а 10 је 60. Потребно је из ових података реконструисати целу серију, знајући да она задовољава својства геометријске прогресије.
Да би се ријешио проблем, потребно је почети писати одговарајући израз за сваког познатог члана. Имамо: а 5 = б 4 * а 1 и а 10 = б 9 * а 1 . Сада поделимо други израз у први, добијамо: а 10 / а 5 = б 9 * а 1 / (б 4 * а 1 ) = б 5 . Дакле, одређујемо именилац, узимајући корен петог степена из односа термина познатих из стања проблема, б = 1.148698. Добијени број се замењује једним од израза за познати елемент, добијамо: а 1 = а 5 / б 4 = 30 / (1,148698) 4 = 17.2304966.
Тако смо нашли оно што је деноминатор прогресије бн једнак, а геометријску прогресију б н-1 * 17,2304966 = а н , где је б = 1,148698.
Где се примењује геометријска прогресија?

Ако у пракси не би било примјене ових серија бројева, онда би се његова студија свела на чисто теоријски интерес. Али таква апликација постоји.

Следе три најпознатија примера:
- Парадокс Зеноа, у којем спретан Ахил не може да ухвати корак са спорим корњачама, решен је коришћењем концепта смањења бесконачног низа бројева.
- Ако ставите зрна пшенице на сваку ћелију шаховске плоче, ставите 1 зрно на 1. ћелију, 2 на 2., 2. на 3. и тако даље, онда вам је потребно 18446744073709551615 зрна да попуните све ћелије плоче!
- У игри "Товер оф Ханои", да би се дискови преуредили са једног на други, потребно је извршити 2 н - 1 операција, односно њихов број расте експоненцијално са бројем кориштених дискова н.