Дивизија је нула. Фасцинантна математика

Број 0 се може представити као нека врста границе која раздваја свет реалних бројева од имагинарних или негативних. Због нејасне позиције, многе операције са овом нумеричком вредношћу нису предмет математичке логике. Немогућност поделе на нулу је живописан пример. А решене аритметичке операције са нулом могу се извршити користећи општеприхваћене дефиниције.

Историја нуле

Нула је референтна тачка у свим стандардним системима рачунања. Европљани су почели да користе овај број релативно недавно, али мудраци Анциент индиа користио нулу за хиљаду година пре него што су европски математичари редовно користили празан број. Чак и пре Индијанаца, нула је била обавезна количина у нумеричком систему Маја. Овај Американац је користио рачун за дуоденал, и са нулом су почели први дан сваког месеца. Занимљиво је да се у Маја знак који означава „нулу“ потпуно поклапа са знаком који дефинише „бесконачност“. Тако су древне Маја закључиле да су те количине идентичне и непознате.

Математичке операције са нулом

Стандардне математичке операције са нулом могу се свести на неколико правила.

Додатак: ако се додаје нула произвољном броју, онда неће променити своју вредност (0 + к = к).

Одузимање: када се одузме нула од било ког броја, вредност одузете остаје непромењена (к-0 = к).

Множење: било који број помножен са 0 даје 0 у производу (а * 0 = 0).

Подела: нула се може поделити било којим бројем који није једнак нули. У овом случају, вредност такве фракције ће бити 0. А подела на нулу је забрањена.

Екпонентиатион. Ова акција се може извршити било којим бројем. Произвољан број подигнут на нулти степен даје 1 (к ⁰ = 1).

Нула је 0 на било који степен (0 ^а = 0).

У овом случају одмах долази до контрадикције: израз 0 ⁰ нема смисла.

Парадокс математике

Чињеница да је подела на нулу немогућа, многи људи знају из школе. Али из неког разлога није могуће објаснити разлог такве забране. У ствари, зашто не постоји формула за подјелу на нулу, али су друге акције са овим бројем сасвим разумне и могуће? Одговор на ово питање дају математичари.

Ствар је у томе да су уобичајене аритметичке операције које ученици уче у основној школи заправо далеко од једнакости у правима, као што нам се чини. Све једноставне операције са бројевима могу се свести на два: збрајање и множење. Ове радње чине суштину самог концепта броја, док се преостале операције заснивају на употреби ова два.

Додавање и множење

Узмите стандардни пример одузимања: 10-2 = 8. У школи се разматра једноставно: ако се из десет предмета одузму два предмета, њих осам остаје. Али математичари гледају на ову операцију сасвим другачије. На крају крајева, таква операција као одузимање за њих не постоји. Овај пример се може написати на други начин: к + 2 = 10. За математичаре, непозната разлика је само број које треба додати на два да би се направило осам. И овде није потребно одузимање, само треба да нађете одговарајућу нумеричку вредност.

Множење и подела се сматрају истим. У Примеру 12: 4 = 3, може се разумети да се ради о подели осам објеката на две једнаке групе. Али у стварности, ово је само обрнута формула записа 3к4 = 12. Такви примјери подјеле могу се дати бескрајно.

Примери поделе са 0

Овде постаје мало јасно зашто је немогуће поделити на нулу. Множење и подела на нулу покорава се сопственим правилима. Сви примјери подјеле ове количине могу бити формулисани као 6: 0 = к. Али ово је обрнути запис израза 6 * к = 0. Али, као што знате, било који број помножен са 0 даје само 0 у производу.Ово својство је својствено самом појму нулте вредности.

Испоставља се да не постоји такав број који, када се помножи са 0, даје било какву опипљиву вредност, односно тај задатак нема решења. Овај одговор се не треба бојати, то је природан одговор за задатке овог типа. Само писање 6: 0 нема смисла, и она не може ништа да објасни. Укратко, овај израз се може објаснити бесмртном "подјелом на нулу".

Да ли постоји операција 0: 0? Заиста, ако је операција множења са 0 легална, може ли се нула поделити са нулом? На крају крајева, једна једнаџба облика 0к 5 = 0 је потпуно легална. Уместо броја 5, можете ставити 0, производ овога се неће променити.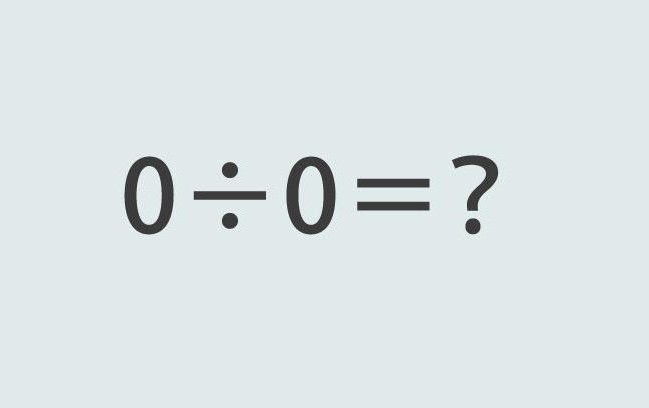

Заиста, 0к0 = 0. Али још увек је немогуће поделити са 0. Као што је поменуто, подела је једноставно инверзно множење. Дакле, ако у примеру 0к5 = 0, морамо одредити други фактор, добијамо 0к0 = 5. Или 10. Или бесконачност. Дељење бесконачности са нулом - како вам се свиђа?

Али ако се било који број уклапа у израз, онда то нема смисла, не можемо изабрати један из бесконачног скупа бројева. Ако је тако, то значи да израз 0: 0 нема смисла. Испоставља се да се и сама нула не може поделити са нулом.

Виша математика

Подела на нулу је главобоља за школску математику. Студирао је на техничким универзитетима математичка анализа мало проширује концепт задатака који немају решење. На пример, до већ познатог израза 0: 0 додају се нове које немају решење у школским курсевима математике:

• бесконачност подељена бесконачно: ∞: ∞;
• бесконачност минус бесконачност: ∞ - ∞;
• јединица подигнута до бесконачне снаге: 1 ^∞ ;
• бесконачност помножена са 0: ∞ * 0;
• неке друге.

Елементарне методе за рјешавање таквих израза је немогуће. Али виша математика, због додатних могућности за низ сличних примјера, даје коначна рјешења. Ово је посебно уочљиво у разматрању проблема из теорије ограничења.

Објављивање несигурности

У теорији граница, вредност 0 се замењује условном бесконачно малом варијаблом. А изрази у којима се подела на нулу добија заменом жељене вредности се конвертују. Испод је стандардни пример откривања лимита коришћењем обичних алгебарских трансформација:

Као што се може видети из примера, једноставна редукција фракција доводи до њене вредности до потпуно рационалног одговора.

Када се разматрају границе тригонометријских функција, њихови изрази имају тенденцију да се сведу на прву изузетну границу. При разматрању граница у којима именитељ прелази на 0 при постављању лимита, користите другу изузетну границу.

Л'Хопитал метод

У неким случајевима, границе израза могу се замијенити границом њихових деривата. Гуиллауме Лопитал - француски математичар, оснивач француске школе математичке анализе. Он је доказао да су границе израза једнаке границама деривата ових израза. У математичком писању, његово правило је следеће.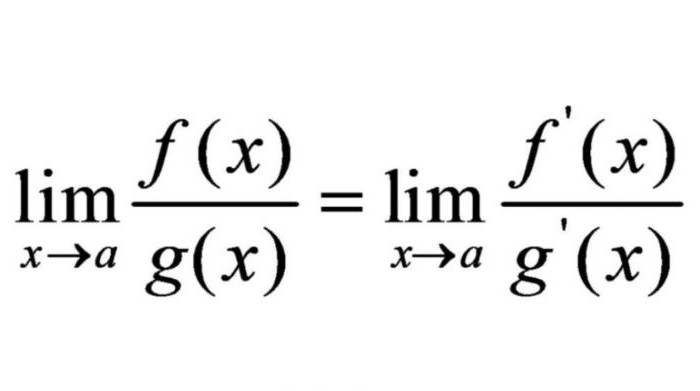

Тренутно се Л'Хопитал метода успјешно користи у рјешавању несигурности типа 0: 0 или ∞: ∞.