Закон о очувању енергије: опис и примјери
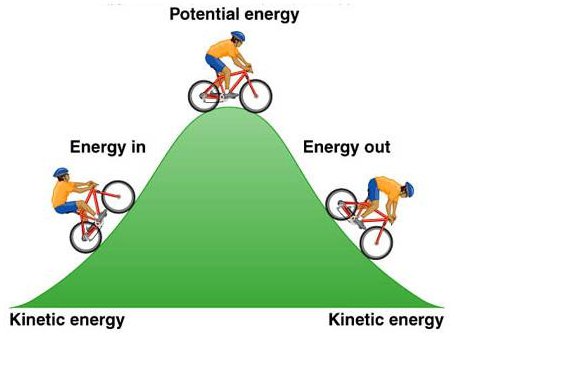
Потенцијална енергија је апстрактна вредност, јер ће сваки објекат који има одређену висину изнад површине Земље већ имати одређену количину потенцијалне енергије. Израчунава се множењем брзине. фрее фалл до висине изнад Земље, као и до масе. Ако се тело креће, можете говорити о присуству кинетичке енергије.
Формула и опис закона
Резултат додавања кинетичке и потенцијалне енергије у систем затворен од спољашњих утицаја, чији делови делују због еластичних сила и силе, не мења се - то је закон очувања енергије у класичној механици. Формула овог закона је следећа: Ек1 + Еп1 = Ек2 + Еп2. Овде је Ек1 кинетичка енергија одређеног физичког тела у одређеном тренутку у времену, а Еп1 је потенцијал. Исто важи и за Ек2 и Еп2, али већ у наредном временском периоду. Али овај закон је истинит само ако је систем у којем функционише затворен (или конзервативан). То сугерише да је вредност пуне механичка енергија не мијења се када на систем дјелују само конзервативне снаге. Када се укључе неконзервативне снаге, део енергије се мења, узимајући друге облике. Такви системи се називају дисипативни. Закон очувања енергије функционише када спољашње силе не утичу на тело.
Ad
Пример закона
Један од типичних примера који илуструје описани закон је експеримент са челичном куглом, који пада на плочу исте супстанце или на стаклу, одбијајући се од ње на приближно исту висину као што је била пре пада. Овај ефекат се постиже захваљујући чињеници да када се објекат креће, енергија се конвертује неколико пута. У почетку, вредност потенцијалне енергије почиње да тежи нули, док се кинетика повећава, али након судара, она постаје потенцијална енергија еластичне деформације кугле.
То се наставља све до тренутка када се објекат потпуно заустави, при чему почиње кретање према горе због сила еластичне деформације плоче и падајућег објекта. Али у исто време долази до акције потенцијалне енергије а. Пошто се лопта разуме на приближно истој висини од које је пала, кинетичка енергија у њој је иста. Поред тога, сума свих енергија које делују на покретни објекат остаје иста током читавог описаног процеса, потврђујући закон очувања укупне механичке енергије.
Ad
Еластична деформација - шта је то?
Да би се у потпуности схватио дати пример, вреди боље разумети шта је потенцијална енергија еластичног тела - овај концепт подразумева поседовање еластичности, која се, када су сви делови датог система деформисани, могу вратити у стање мировања, радећи неке послове на телима са којима физички функционишу. предмет. На рад сила еластичности не утиче облик путање кретања, јер рад на рачун њих зависи само од положаја тела на почетку и на крају покрета.
Када су спољашње силе

Али закон конзервације се не односи на стварне процесе у којима је укључена сила трења. Пример је падни предмет на земљи. Током судара кинетичка енергија и снага отпора се повећава. Овај процес се не уклапа у оквир механике, јер се температура тијела повећава због повећане отпорности. Из наведеног произилази да закон о уштеди енергије у механици има озбиљна ограничења.
Ad
Термодинамика
Први закон термодинамике каже: разлика између количине топлоте акумулиране услед рада на спољним објектима је једнака промени унутрашња енергија овај не-конзервативни термодинамички систем.
Али ова тврдња се најчешће формулише у другачијој форми: количина топлоте добијене термодинамичким системом троши се на рад на објектима изван система, као и на промену количине енергије унутар система. Према овом закону, он не може нестати, прелазећи из једног облика у други. Из тога следи да је стварање машине која не троши енергију (такозвани перпетуум мобиле) немогуће, јер ће систему требати енергија извана. Али многи су и даље упорно покушавали да га створе, не узимајући у обзир закон о очувању енергије.
Пример манифестације закона конзервације у термодинамици
Експерименти показују да термодинамички процеси не могу бити обрнути. Примјер за то је контакт тијела с различитим температурама, при чему ће се више загријавати, а друга је примити. Обрнути процес је у принципу немогућ. Други пример је пренос гаса са једног дела брода на други након отварања преграде између њих, под условом да је други део празан. Супстанца у овом случају никада неће почети спонтано да се креће у супротном смеру. Из наведеног следи да сваки термодинамички систем тежи ка стању мировања, у коме су његови појединачни делови у равнотежи и имају исту температуру и притисак.
Ad
Хидродинамика
Примена закона конзервације у хидродинамичким процесима је у принципу изражена, описан од стране Бернулија. Звучи овако: сума притиска и кинестетичке и потенцијалне енергије по јединици запремине је иста у било којој датој тачки протока течности или гаса. То значи да је за мерење протока довољно измерити притисак на две тачке. То се, по правилу, ради са манометром. Међутим, Бернулијев закон важи само ако течност у питању има вискозност која је нула. Да би се описао ток реалних флуида, користи се Бернулијев интеграл, што подразумева додавање термина који узимају у обзир отпорност.
Електродинамика
Приликом електрификације два тела, број електрона у њима остаје непромењен, због чега је позитивни набој једног тела једнак у односу на негативни набој другог. Према томе, закон очувања електричног набоја сугерише да се у електрично изолованом систему сума набоја његових тела не мења. Ова тврдња је такође тачна када се наелектрисане честице претворе у трансформације. Тако, када се сударају 2 неутрално набијене честице, сума њихових набоја и даље остаје нула, јер се позитивно набијена честица појављује заједно са негативно набијеном честицом.
Ad
Закључак

Закон очувања механичке енергије, момента и момента - основни физички закони повезани са хомогеношћу времена и његовом изотропијом. Они нису ограничени само на оквире механике и примјењиви су како на процесе који се одвијају у вањском простору, тако и на квантне појаве. Закони очувања омогућавају добијање података о различитим механичким процесима без њиховог проучавања помоћу једнаџби кретања. Ако неки процес у теорији игнорише ове принципе, онда је спровођење експеримената у овом случају бесмислено, јер ће бити неефикасни.