Екстремне функције. Како пронаћи?

Математичка анализа - ово је прилично забаван део математике, са којим се суочавају апсолутно сви студенти и студенти. Ипак, сви не воле Матан. Неки можда не разумију ни елементарне ствари као што је наизглед стандардна студија функције. Циљ овог чланка је да исправи такву грешку. Желите ли знати више о анализи функције? Желите ли знати које су то точке екстремитета и како их пронаћи? Онда је овај чланак за вас.

Проучавање графова функција

Прије свега, вриједи разумјети зашто је потребно анализирати графикон. Постоје једноставне функције за цртање које није тешко. Парабола може послужити као јасан примјер такве функције. Нацртајте њен распоред није тешко. Све што је потребно је пронаћи бројеве за које функција узима вриједност користећи једноставну трансформацију.А у принципу, то је све што је потребно цртати да би се нацртао граф параболе.

Али шта ако је функција чије графове требамо цртати много тежа? Пошто су својства комплексних функција прилично нејасна, потребно је извршити читаву анализу. Тек тада се функција може графички приказати. Како то учинити? Одговор на ово питање можете наћи у овом чланку.

План анализе функција

Прва ствар коју треба урадити је да се проведе површна студија функције, током које ћемо наћи домен дефиниције. Почнимо редом. Домен дефиниције је скуп вриједности по којима је функција специфицирана. Једноставно речено, ово су бројеви који се могу користити у функцији умјесто к. Да би се одредио опсег, потребно је само погледати унос. На пример, очигледно је да је функција и (к) = к ³ + к ² - к + 43 домен дефиниције скуп реалних бројева. Па, са функцијом као што је (к ² - 2к) / к, све је мало другачије. Пошто број у имениоцу не сме бити 0, област функције ће бити сви реални бројеви, поред нуле.

Затим морате да пронађете такозване функцијске нуле. То су вриједности аргумента за које цијела функција узима вриједности нула. Да би се то урадило, потребно је изједначити функцију са нулом, размотрити је детаљно и извршити неке трансформације. Узмите функцију и (к) = (к ² - 2к) / к која нам је већ позната. Из школског курса знамо да је фракција 0 када је нумератор нула. Зато одбацујемо именитељ и почињемо да радимо са нумератором, изједначавајући га са нулом. Добијамо к ² - 2к = 0 и стављамо к за заграде. Дакле, к (к - 2) = 0. Као резултат тога, налазимо да је наша функција нула када је к једнако 0 или 2.

Екстремне тачке на графу функција

Током проучавања графа функције, многи се суочавају са проблемом у облику екстремних тачака. И то је чудно. Уосталом, екстреми су прилично једноставна тема. Не верујете? Увјерите се сами читајући овај дио чланка, у којем ћемо говорити о точкама минимума и максимума.

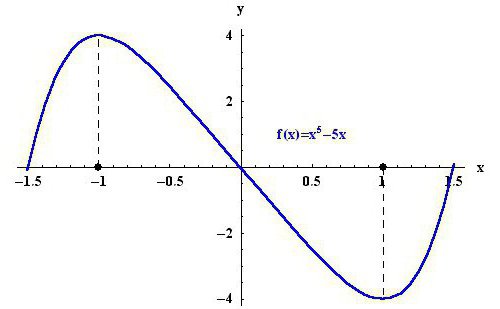
Започети је да схватите шта представља екстрем. Екстрем је гранична вриједност коју функција досеже на графу. Одавде се испоставља да постоје две екстремне вредности - максимум и минимум. Ради јасноће, можете погледати слику изнад. На истраживаном подручју, тачка -1 је максимум функције и (к) = к ⁵ - 5к, а тачка 1, односно, је минимална.

Такође, немојте бркати појмове. Екстремне тачке функције су они аргументи на којима одређена функција преузима екстремне вредности. Заузврат, екстрем је вриједност минима и максима функције. На пример, поново размотрите слику изнад. -1 и 1 су екстремне тачке функције, а 4 и -4 су саме крајности.

Финдинг Ектреме Поинтс

Али како да нађемо екстремне тачке функције? Прилично је једноставно. Прва ствар коју треба учинити је пронаћи дериват једнаџбе. Претпоставимо да имамо задатак: "Нађите екстремне тачке функције и (к), к је аргумент. За јасноћу, узмемо функцију и (к) = к ³ + 2к ² + к + 54. Хајде да диференцирамо и добијемо следећу једначину: 3к ² + 4к + 1. На крају смо добили стандард квадратна једначина. Следеће је само да се изједначи са нулом и да се пронађу корени. Пошто је дискриминантни већи од нуле (Д = 16 - 12 = 4), ова једначина је дефинисана са два корена. Пронађите их и добијте две вредности: 1/3 и -1. То ће бити екстремне тачке функције. Међутим, како се утврди ко је ко? Која је тачка максимум а која је минимална? Да бисте то урадили, узмите следећу тачку и сазнајте њену вредност. На пример, узмите број -2, који је лево од координатне линије од -1. Ову вредност замењујемо нашом једначином и (-2) = 12 - 8 + 1 = 5. Као резултат, добили смо позитиван број. То значи да се на интервалу од 1/3 до -1 функција повећава. Ово, заузврат, значи да у интервалима од минус бесконачности до 1/3 и од -1 до плус бесконачности, функција се смањује. Дакле, можемо закључити да је број 1/3 минимална тачка функције на испитиваном интервалу, а -1 је максимална тачка.

Збир екстремних тачака функције

Такође је важно напоменути да је не само неопходно наћи екстремне тачке на УСЕ, већ и извршити неку врсту операције са њима (додати, множити, итд.). Из тог разлога треба посветити посебну пажњу условима овог проблема. Уосталом, због непажње, можете изгубити бодове.