Пронаћи корен једначине? То је лако!

У математици постоји низ једнаџби. Они увек треба да буду решени, тј. Да траже све бројеве који ће га учинити истинском једнакошћу. Начини проналажења решења одређени су оригиналним обликом једначине. Из ње ће зависити од броја правих вредности варијабле, које су означене као корен једначине. Овај број може варирати од нуле до бесконачности.

Шта се подразумева под једначином и њеним кореном?

Из наслова је јасно да изједначава две вредности које могу бити представљене нумеричким или абецедним изразима. Поред тога, оне садрже још непознате количине. Најједноставнија једначина има само једну.

Постоји велики број типова једначина, али концепт корена за њих је увек исти. Корен једначине је таква вредност непознатог броја на којој једначина претпоставља истинску једнакост. Постоје ситуације када постоји неколико таквих бројева, а непознато се зове варијабла.

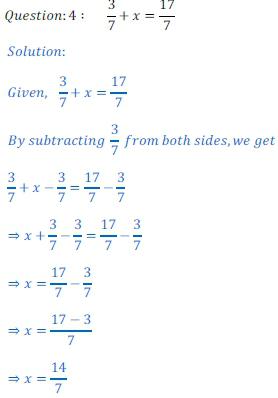
Проналажење свих могућих коријена једнаџбе је његово рјешење. То значи да морате да извршите низ математичких операција које га поједностављују. И онда водимо ка једнакости, која садржи само непознато и број.

У алгебри, када се решавају једначине, може се доћи до ситуације да уопште неће бити корена. Онда кажу да је нерјешив. И у одговору такве једначине потребно је написати да не постоје решења.

Али понекад се деси супротно. То јест, страни процеси настају у процесу бројних трансформација. Они неће дати истинску једнакост приликом замјене. Стога, бројеве треба увек проверавати да би се избегла ситуација са непотребним коренима у одговору. У супротном, једначина се неће сматрати решеном.

О линеарној једначини

Она се увек може трансформисати у запис следећег облика: а * к + в = 0. У њему, “а” је увек не-нула. Да би се разумело колико корена има једна једнаџба, мораће да буде решено у општој форми.

Трансформације алгоритма:

• премјестити појам “у” на десну страну једнакости, замјењујући његов знак супротним;
• поделити обе стране резултирајуће једнакости коефицијентом “а”.

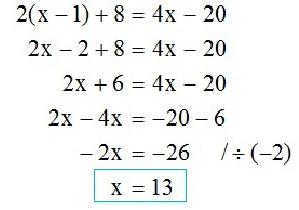
Општи поглед на решење је:

к = -ин / а .

Из тога је јасно да је одговор један број. То је само један коријен.

Куадратиц екуатион

Њен општи облик: а * к ² + б * к + ц = 0 . Овде су коефицијенти било који бројеви осим првог, “а”, који не могу бити једнаки нули. На крају крајева, аутоматски ће постати линеаран. Одговор на питање колико коријена има једнаџба више није тако јасан као у претходном случају.

Све ће зависити од вредности дискриминанта. Израчунава се по формули Д = у ² - 4 а * с . Након израчунавања, "Д" може бити више, мање или једнако нули. У првом случају, корени једначине ће бити два, у другом ће одговор бити „без корена“, а трећа ситуација ће дати само једну непознату вредност.

Формуле које се користе за проналажење корена квадратне једначине и садрже дискриминант

У општем случају, када је "Д" позитиван број, није једнак нули, треба да користите следећу формулу:

х _1,2 = (-в ± )Д) / (2 * а) .

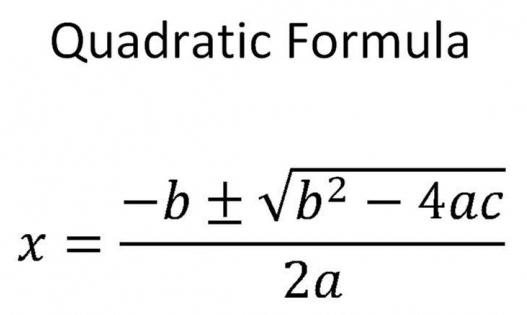
Овде увек постоје два одговора. То је због чињенице да је оригинална формула знак плус / минус. Значајно мења вредност непознатог.

Када је "Д" једнако нули, корен једначине је једини број. Само зато скуаре роот од нуле је нула. Дакле, додавање и одузимање ће морати бити нула. Из овог броја неће се променити. Стога се формула коријена једнаџбе може написати без спомињања "Д":

к = (-в) / (2 * а).

Ако је дискриминант негативан, није могуће извадити квадратни корен из њега. Дакле, корени такве једначине неће бити.

Ремарк То важи за школски курс који се не учи. комплексни бројеви. Када се уђу, испада да ће у овој ситуацији бити два одговора.

Формуле за израчунавање корена квадратне једначине које не користе дискриминантно

Говоримо о теореми Виета. Важи у случају када је квадратна једначина записана у нешто другачијој форми:

к ² + ц * к + ц = 0.

Онда је коријенска формула квадратна једначина своди се на испуњење решења два линеарна:

к ₁ + к ₂ = -ин
и
к ₁ * к ₂ = с.

Решава се због чињенице да је израз за један од корена изведен из првог. Ова вредност мора бити замењена другом. Тако да ће други коријен бити пронађен, а затим први.

Ова опција увек може доћи из опште форме квадратне једначине.

Довољно је поделити све коефицијенте на "а".

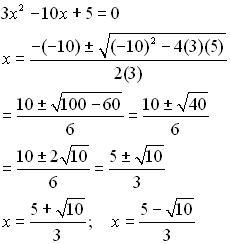
Шта ако треба да знате најмању вредност корена?

Решите једначину и пронађите све могуће бројеве који су прикладни за одговор. И онда изаберите најмањи. Ово ће бити најмањи корен једначине.

Најчешће се таква питања налазе у задацима који имају степен већи од 2, или садрже тригонометријске функције. Пример када треба да пронађете најмањи корен је следећа једнакост:

2 к ⁵ + 2 к ⁴ - 3 к ³ - 3 к ² + к + 1 = 0.

Да би се пронашла свака вредност која се може назвати "корен једначине", ова једначина се мора трансформисати. Прва акција: груписати чланове у пару: прва са другом и тако даље. Онда из сваког пара направите заједнички фактор.

У свакој загради ће остати (к + 1). Заједнички фактор у првом пару ће бити 2 к ⁴ , у другом 3 к ² . Сада морате поново да поставите заједнички фактор, који ће бити исти.

Након множитеља (к + 1) биће (2 к ⁴ - 3 к ² + 1). Продукт два фактора једнак је нули, само ако један од њих узима вредност једнаку нули.

Прва заграда је нула за к = -1. Ово ће бити један од корена једначине.

Други ће бити добијени из једначине коју формира друга заграда, изједначена са нулом. То је бикуадратиц. Да бисте га решили, потребно је да унесете нотацију: к ² = и. Тада ће се једначина значајно променити и узети уобичајени облик квадратне једначине.

Његов дискриминант је Д = 1. Већи је од нуле, што значи да ће постојати два корена. Први коријен је једнак 1, други ће бити 0,5. Али то су вредности за и.

Потребно је вратити се на унесену ознаку. к _1.2 = ± 1, к _3.4 = ± .0.5. Сви корени једначине: -1; 1; -√0.5; .50.5. Најмањи од њих је -1. Ово је одговор.

Као закључак

Подсетник: све једначине треба проверити да ли је корен одговарајући. Можда је он странац? Вриједи провјерити предложени примјер.

Ако заменимо јединицу у почетно датој једначини уместо "к", онда се испостави да је 0 = 0. Овај корен је тачан.

Ако је к = -1, резултат је исти. Коријен је такође погодан.

Слично томе, када су вредности "к" једнаке анд0.5 и .50.5, истинска једнакост поново излази. Сви корени се уклапају.

Овај пример није дао корене. То није увијек случај. Могло би се десити да најмања вредност не би била погодна за тестирање. Онда бих морао да изаберем од осталих.

Закључак: потребно је запамтити о провјери и пажљиво приступити рјешењу.