Четири формуле помоћу којих можете израчунати површину ромба. Диамонд пропертиес

Ромб је посебна фигура у геометрији. Због својих посебних својстава не постоји једна, већ неколико формула помоћу којих се израчунава површина ромба. Које су то особине и које су најчешће формуле за проналажење подручја ове фигуре? Да видимо.

Који геометријски облик зове се дијамант

Пре него што сазнате која је површина ромба, вреди знати каква је то фигура.

Од времена еуклидске геометрије, ромб се зове симетрични четвороугао, чије су све четири стране једнаке дужине и паралелне у паровима.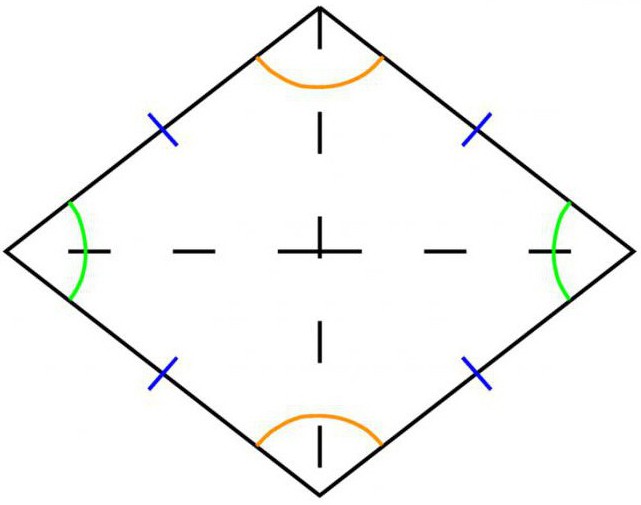

Порекло термина

Име ове фигуре дошло је до најсавременијих језика из грчког, посредством латинског. "Претеча" речи "ромб" постала је грчка именица μομβος (тамбурина). Иако су становници двадесетог века, навикнути на округле тамбурине, тешко замислити их другачијег облика, али Хелени су традиционално ове музичке инструменте чинили не округлим, већ дијамантским.

На већини модерних језика овај математички израз се користи, као што је на латинском језику: ромбус. Међутим, на енглеском језику, дијаманти се понекад називају и дијамант (дијамант или дијамант). Ова фигура је добила такав надимак због свог посебног облика, налик драгоцјеном камену. По правилу, такав термин се не користи за све дијаманте, већ само за оне чији је угао пресека између две стране шестдесет или четрдесет пет степени.

По први пут ова фигура се спомиње у списима грчког математичара, који је живио у првом веку нове ере - чапљу Александрије.

Које особине има ова геометријска фигура?

Да бисте пронашли подручје ромба, прво морате знати које значајке има ова геометријска фигура.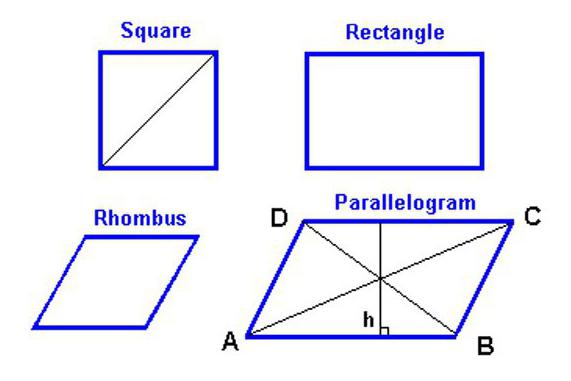

• Као што је већ поменуто у дефиницији ромба, то је четвороугао. И из разлога што су његове супротне стране у пару паралелне једна другој, ромб се може назвати и паралелограм, што значи да се на њега односи већина својстава ове фигуре.
• Оба дијагонална ромба на његовом месту пресека су подељена на два дела. И због чињенице да се укрштају под углом од деведесет степени, дијагонале деле слику на 4 рецтангле триангле.
• У сваком ромбу, дијагонале раздвајају углове на два дела, а истовремено су и њихове симетрале.
• Ако је свака од двију дијагонала ромба подигнута на снагу квадрата, тада ће њихова сума бити једнака производу квадрата стране ове фигуре и броја четири.
• Ако повежете линије средине четири стране ромба, резултат ће бити правоугаоник.
• Ако је круг уписан у дијамант (без обзира на његове углове), онда ће се његова централна тачка подударати са центром пресека дијагонала.
• Дијагонални дијаманти у контакту са осима своје симетрије на угловима од деведесет степени.
• Пошто су све стране ромбова међусобно идентичне дужине, његов периметар се израчунава по формули П = 4 к К (К је дужина једне од страна).

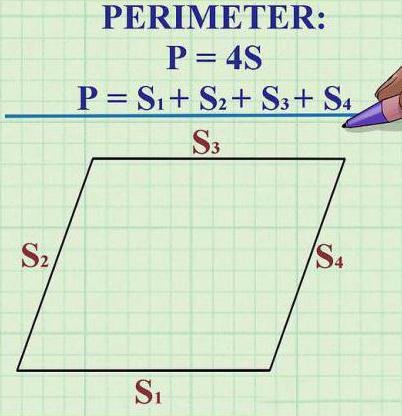
Под којим условима је паралелограм дијамант

Као што знате, сваки ромб је паралелограм, али није сваки паралелограм ромб. Да би се тачно тврдило да је приказана фигура заиста ромб, а не једноставни паралелограм, она мора одговарати једној од три главне карактеристике које разликују ромб. Или све три одједном.

1. Дијагонални паралелограм се укршта под углом од 90 степени.
2. Дијагонале раздвајају углове на два дела, дјелујући као њихови симетрали.
3. Не само паралелне, већ и суседне стране имају исту дужину. То је, узгред, једна од главних разлика између ромба и паралелограма, јер друга фигура има само паралелне стране, али не и сусједне.

Под којим условима је квадрат ромб

Према својим својствима, у неким случајевима ромб може истовремено постати квадрат. Да бисте јасно потврдили ову тврдњу, једноставно окрените квадрат у оба смера за четрдесет пет степени. Резултат ће бити дијамант, чији је сваки од углова деведесет степени.

Такође, да би потврдили да је квадрат ромб, можете упоредити знакове ових фигура: у оба случаја, све стране су једнаке, а дијагонале су бисектрике и секу се под углом од 90 степени.

Како пронаћи подручје ромба користећи његове дијагонале

У савременом свету на интернету можете наћи скоро све материјале за обављање потребних прорачуна. Дакле, постоји маса ресурса опремљених програмима за аутоматско рачунање површине одређеног облика. Штавише, ако (као у случају ромба) постоји неколико формула за то, онда постоји могућност да се изабере који од њих је најпогоднији за употребу. Међутим, пре свега, неопходно је бити у стању да израчуна површину ромба без помоћи компјутера и да буде оријентисан у формулама. За дијамант има много, али најпознатији од њих су четири.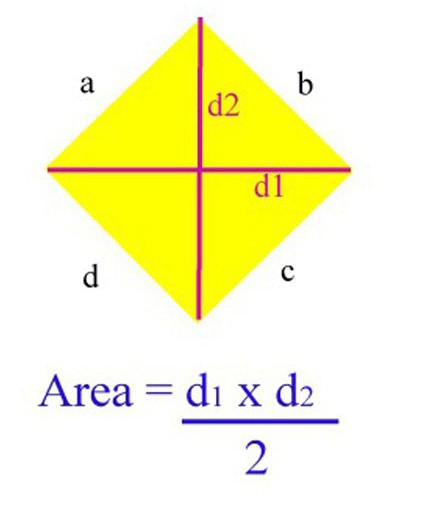

Један од најлакших и најчешћих начина да се открије подручје ове фигуре, ако постоје информације о дужини његових дијагонала. Ако проблем има ове податке, у овом случају можете примијенити сљедећу формулу како бисте пронашли подручје: С = КМ к ЛН / 2 (КМ и ЛН су дијагонала КЛМН ромб).

У пракси можете проверити ваљаност ове формуле. Претпоставимо да КЛМН ромб има једну дијагоналу КМ, а његова дужина је 10 цм, а друга ЛН 8 цм, а затим их замењујемо горњом формулом и добијамо следећи резултат: С = 10 к 8/2 = 40 цм2.

Формула за израчунавање површине паралелограма

Постоји још једна формула. Као што је већ поменуто у дефиницији ромба, он није само четвороугао, већ и паралелограм, и има све карактеристике овог облика. У овом случају, да би се пронашла његова површина, разумно је користити формулу која се користи за паралелограм: С = КЛ к З. У овом случају, КЛ је дужина паралелограмске стране (ромб), а З је дужина висине повучене на ову страну.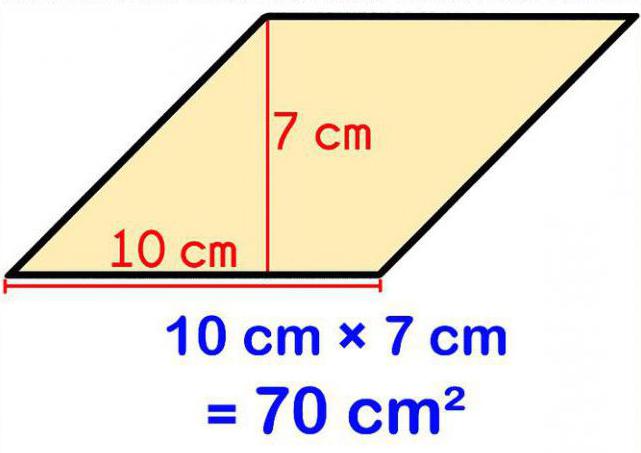

Код неких задатака није дата дужина стране, али је познат периметар дијаманта. Пошто је формула за налажење горе наведена, може се користити за проналажење дужине стране. Дакле, периметар је 10 цм, а дужина стране се може препознати обртањем периметарске формуле и поделом 10 на 4. Резултат ће бити 2,5 цм - то је жељена дужина ромбове стране.

Сада је вредно покушати да се тај број замени у формули, знајући да је дужина са стране такође 2,5 цм, а сада ћемо покушати да ове вредности убацимо у горе поменуту формулу паралелограма. Показало се да је површина ромба С = 2,5 к 2,5 = 6,25 цм2.

Други начини за израчунавање површине дијаманта

Они који су већ овладали синусима и косинусима могу користити формуле које их садрже да би пронашли подручје ромба. Класичан примјер је сљедећа формула: С = КМ ² к Син КЛМ. У овом случају, површина фигуре је једнака производу две стране ромба помноженом са синусом угла између њих. Пошто су у ромбу све стране исте, лакше је одмах произвести једну страну у квадрату, као што је приказано у формули.

Проверавамо ову шему у пракси, а не само на ромбу, већ на квадрат, који, као што је добро познато, има све углове равно, што значи да су деведесет степени. Претпоставимо да је једна од страна 15 цм, а познато је и да је синус од 90 ° један. Затим, према формули, С = 15 к 15 к Син 90 ° = 255к1 = 255 цм2 ^.

Поред горе наведеног, у неким случајевима се користи и друга формула, користећи синус за одређивање површине ромба: С = 4 к Р ² / Син КЛМ. У овој варијанти користи се радијус кружнице уписане у дијамант. Она се уздиже до квадрата и множи са четири. И цео резултат је подељен синусом угла који се налази поред уписане фигуре.

Као пример, за једноставност израчунавања поново ћемо узети квадрат (синус његовог угла увек ће бити једнак једном). Радијус кружнице исписан у њој износи 4,4 цм, а затим се површина ромба израчунава на следећи начин: С = 4 к 4,4 ² / Син 90 ° = 77,44 цм ²

Наведене формуле за проналажење радијуса ромба су далеко од једине такве врсте, али су најлакше разумјети и провести израчунавања.