Виша математика: раван у простору

Други после праве линије је важан елемент просторне геометрије. Способност да се опише једнаџбом омогућава израчунавање просторних углова и висина за различите тродимензионалне облике. У овом чланку дајемо све врсте једначина које описују раван у простору. Такође размотрите могуће опције за међусобно распоређивање авиона.

Геометријски концепт авиона

У дводимензионалној геометрији, равнина се не разматра, јер се сви проблеми рјешавају само у к и и координатама. Када додамо трећу координатну осу з, равнина постаје важан геометријски елемент.

Термин "авион" се схвата као скуп тачака, од којих свака два, ако је повезан, резултујући вектор ће увек бити окомит на неки дати вектор. Овај дати вектор се назива нормалним. Нормална игра важну улогу у нумеричком опису равнине, а њена својства се користе за рјешавање различитих проблема.

На доњој слици приказане су три равни у простору (плава) које се укрштају у четвртој (црвеној) слици.

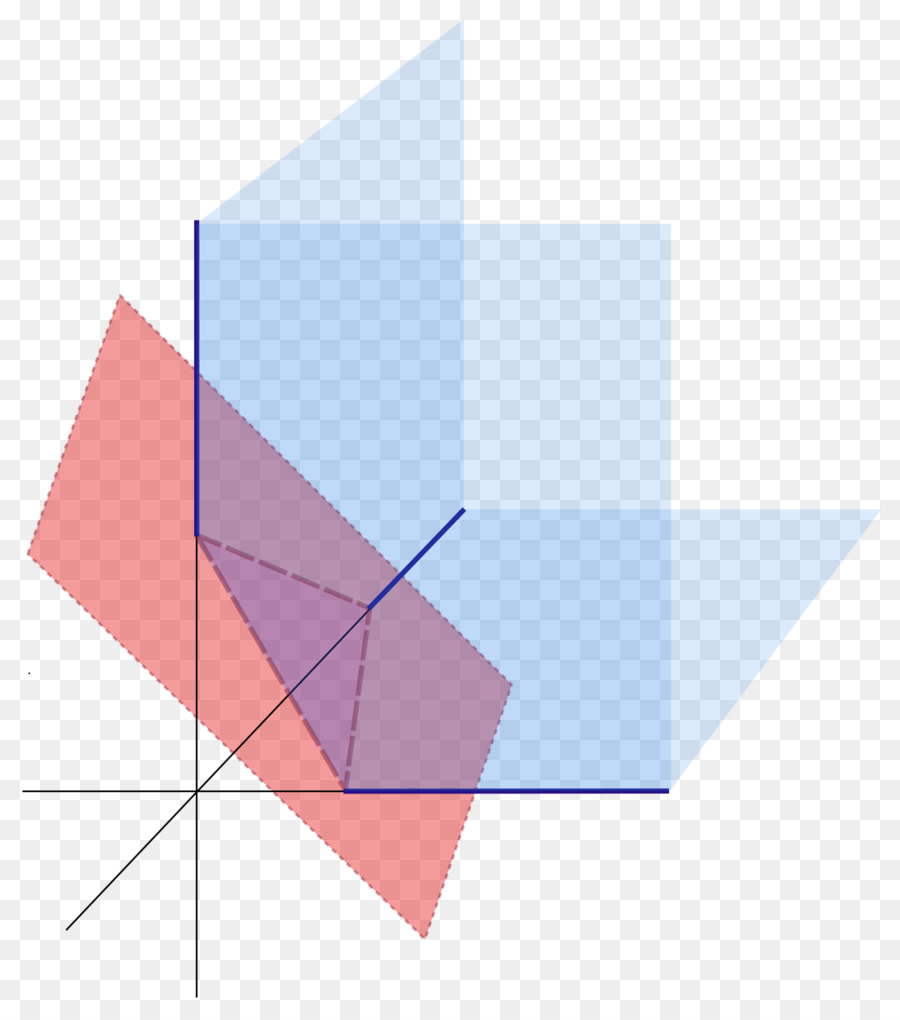
Генерал екуатион

Горња дефиниција ће помоћи да добијемо једначину за равнину у простору у координатама. Претпоставимо да постоји нека тачка са познатим координатама К (к ₀ ; и ₀ ; з ₀ ). Познато је да лежи у одређеној равни, којој је норма једнака н¯ (А; Б; Ц). Претпоставимо сада да произвољна тачка М (к; и; з) такође припада овој равни. Ово последње значи да ће вектори КМ и нп бити окомити, тј. Њихов скаларни производ нестаје. Зато можемо да напишемо следећу једнакост:

(КМ¯ * н¯) = 0.

Замењујући координате у њу и отварајући заграде, долазимо до једначине:

(кк ₀ ) * А + (ии ₀ ) * Б + (зз ₀ ) * Ц = 0 =>

А * к + Б * и + Ц * з + Д = 0, где Д = -1 * (А * к ₀ + Б * и ₀ + Ц * з ₀ ).

Резултат једначине за раван се назива генерал. Она има исту форму као и општа једначина за директну једначину на равни. Може се видјети да су коефицијенти који се суочавају са варијаблама к, и и з ништа више од координата окомите равнине вектора. Зове се режија.

Имајте на уму да ако је, док добијамо општу једначину, одређена тачка К непозната, а постоји само вектор правца нп, онда долазимо до једначине за скуп паралелних равни које се разликују само у параметру Д.

Партиал екуатион

Када се приказују равни у простору, када су дате специфичне оси координата, најлакше је одржавати геометријске конструкције ако постоје тачке у којима се раван сијече ове осе. Израз који вам омогућава да сазнате координатне вредности пресека равни са к, и и з осама се назива интервална једначина. То се може постићи извођењем неких математичких трансформација са општом једначином.

Претпоставимо да је следећа једначина позната:

А * к + Б * и + Ц * з + Д = 0.

Пренесите слободни појам Д на десну страну једначине, а затим поделите обе стране једначине тако да је јединица на десној страни. Имамо:

А * к + Б * и + Ц * з = -Д =>

к / (- Д / А) + и / (- Д / Б) + з / (- Д / Ц) = 1 или

к / п + и / к + з / р = 1, где је п = -Д / А, к = -Д / Б, р = -Д / Ц.

Резултирајући израз се назива једначином у сегментима, а дужине сегмената који су одсечени на оси к, и и з, почевши од тачке (0; 0; 0), имају вредности п, к, и р, респективно. Ово се може проверити на следећи начин: ако претпоставимо да су координате дуж и осе и з нуле, онда се добија к једнако к. То јест, тачка пресека са к-осом има координате (п; 0; 0). Слично томе, тврдећи, добијамо преостале две координате (0; к; 0) и (0; 0; р).

Параметарска векторска једначина

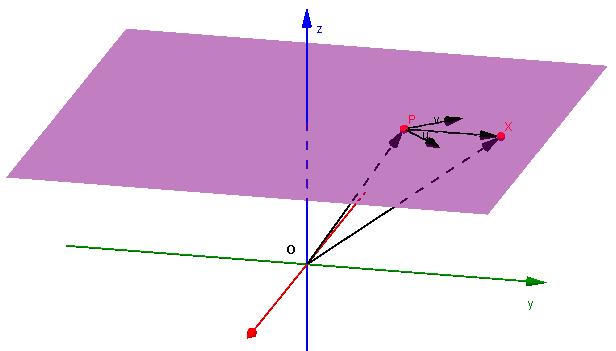
Ово је трећи важан тип једначине, који се такође често користи у решавању проблема. Горе је показано да је равнина јединствено дефинисана тачком и нормалним вектором. Међутим, могуће је одредити овај геометријски дводимензионални објект на другачији начин.

Претпоставимо да постоје два копланарна вектора који нису паралелни један другом. Ми их означавамо са у¯ (а ₁ ; б ₁ ; ц ₁ ) и в¯ (а ₂ ; б ₂ ; ц ₂ ). Точка К (к ₀ ; и ₀ ; з ₀ ) је такође позната. Која ће бити једнаџба равнине која пролази кроз ову тачку и два вектора?

На ово питање можете одговорити тако што ћете добити једнаџбу уопште. Међутим, овај проблем ћемо решити на други начин. Подсјетимо се да било који вектор равнине може да се разложи на два друга копланарна вектора, који такође припадају овој равни. То значи да је произвољни вектор КП¯, где је П (к; и; з), представљен као:

КП¯ = α * у¯ + β * в¯.

Пролазећи кроз све тачке П у равни, добијамо одговарајуће параметре α и β. Једначина дата за раван се назива параметријски векторски. Често се снима у координатном облику:

(к; и; з) = (к ₀ ; и ₀ ; з ₀ ) + α * (а ₁ ; б ₁ ; ц ₁ ) + β * (а ₂ ; б ₂ ; ц ₂ ).

Може се видјети да је овај облик писања сличан векторској једнаџби за правац у дводимензионалним и тродимензионалним случајевима.

Овај израз се може експлицитније написати раздвајањем варијабли:

к = к ₀ + α * а ₁ + β * а ₂ ;

и = и ₀ + α * б ₁ + β * б ₂ ;

з = з ₀ + α * ц ₁ + β * ц ₂ .

Ове три једначине имају облик сличан параметарској једначини за правац у простору. Овај тип се често користи приликом конверзије векторске једначине у заједничку равнину.

Паралелне равни

Постоје само две опције за релативни положај две равни у простору. У овом делу чланка дајемо стање када су паралелне.

Ако су две једначине у равни дате у општој форми, онда је њихов паралелизам прилично једноставан. Две равни ће бити паралелне ако су њихови вектори такви водичи. Претпоставимо да постоје две једначине:

А ₁ * к + Б ₁ * и + Ц ₁ * з + Д ₁ = 0;

А ₂ * к + Б ₂ * и + Ц ₂ * з + Д ₂ = 0.

Окомито на сваку од равнина вектора су координате:

н ₁ ¯ (А ₁ ; Б ₁ ; Ц ₁ );

н ₂ ¯ (А ₂ ; Б ₂ ; Ц ₂ ).

Ако вектор н ₁ ¯ може бити представљен као множење реалним бројем вектора н ₂ ¯, онда ће оба бити паралелна, односно:

н ₂ ¯ = л * н ₁ ¯, где је л прави број.

Други начин да се одреди њихов паралелизам је да се пронађе косинус кута између њих кроз скаларни производ и модуле вектора. Овај косинус треба да буде једнак јединству, онда ће вектори (равни) бити паралелни. Одговарајућа формула је:

цос (=) = | (н ₁ ¯ * н ₂ ¯) | / (| н ₁ ¯ | * | н ₂ ¯ |) = 1.

Ако су једнаџбе равнина дате у параметарском векторском облику, онда се паралелизам у простору равнина одређује и из услова паралелизма нормала према њима. Да бисмо пронашли правце вектора ових нормала, треба узети векторске производе вектора који формирају сваку равнину.

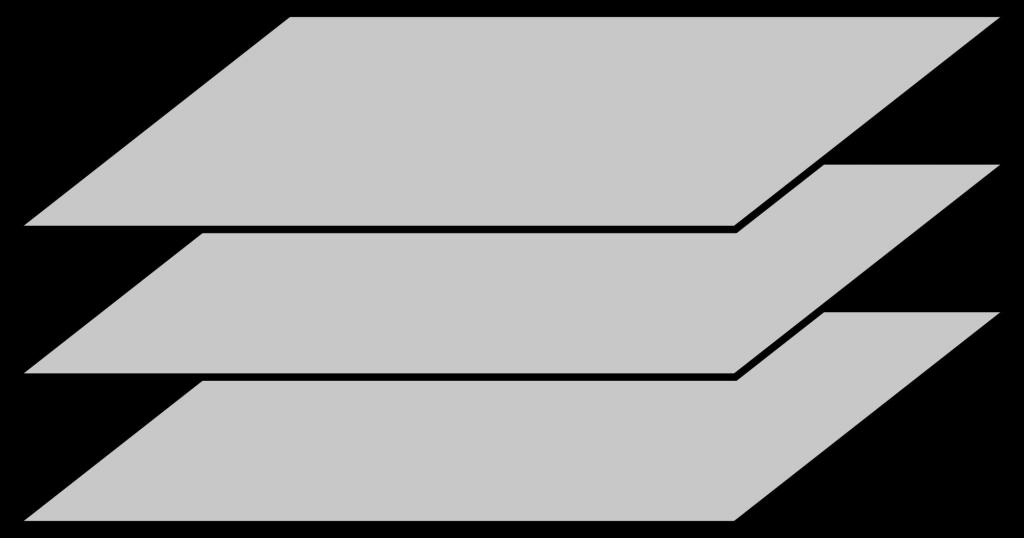
На слици изнад приказане су три равни које су паралелне једна другој.

Пресијецање равнина

Ово је друга верзија међусобног распореда у простору авиона. У овом случају, две равни се секу дуж неке праве линије која им припада. У овом случају, важно је бити у стању да израчуна дијалогни угао овог пресека. Увек је једнак углу између одговарајућих водећих вектора, тј. Између вертикала равни.

У претходном параграфу већ је дата формула која омогућава израчунавање угла између нормала. Овдје ћемо је отворити само писањем координата вектора н ₁ ¯ и н ₂ ¯:

ар = арццос (| А ₁ * А ₂ + Б ₁ * Б ₂ + Ц ₁ * Ц ₂ | / (А (А ₁ ² + Б ₁ ² + Ц ₁ ² ) * √ (А ₂ ² + Б ₂ ² + Ц ₂ ² ))).

Ова формула се често користи за израчунавање дводимензионалних углова између равнина пирамиде или нагнуте призме.

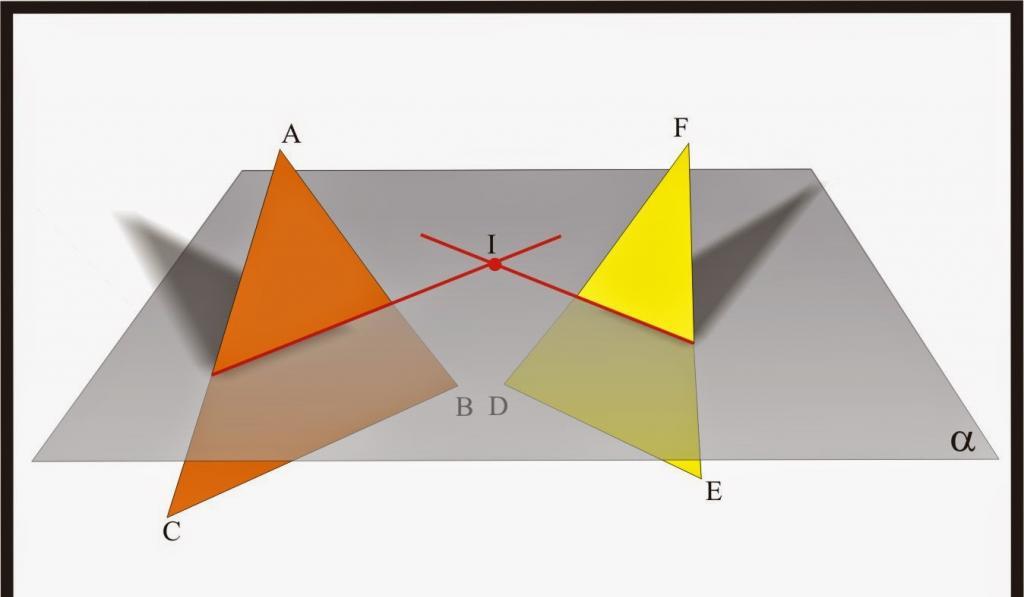
Две равни које секу трећу хоризонталну су приказане на слици горе.

Посебан случај пресека две равни је угао 90 = 90 ^о , тј. Постоји окомитост разматраних геометријских објеката. Да би се одредила перпендикуларност, није неопходно израчунати угао тхе користећи горе помало компликовану формулу, јер ће за то бити довољно израчунати вредност скаларног производа н ₁ ¯ и н ₂ ¯. За окомите равни, то је нула, то јест:

(н ₁ ¯ * н ₂ ¯) = А ₁ * А ₂ + Б ₁ * Б ₂ + Ц ₁ * Ц ₂ = 0.

Сноп авиона

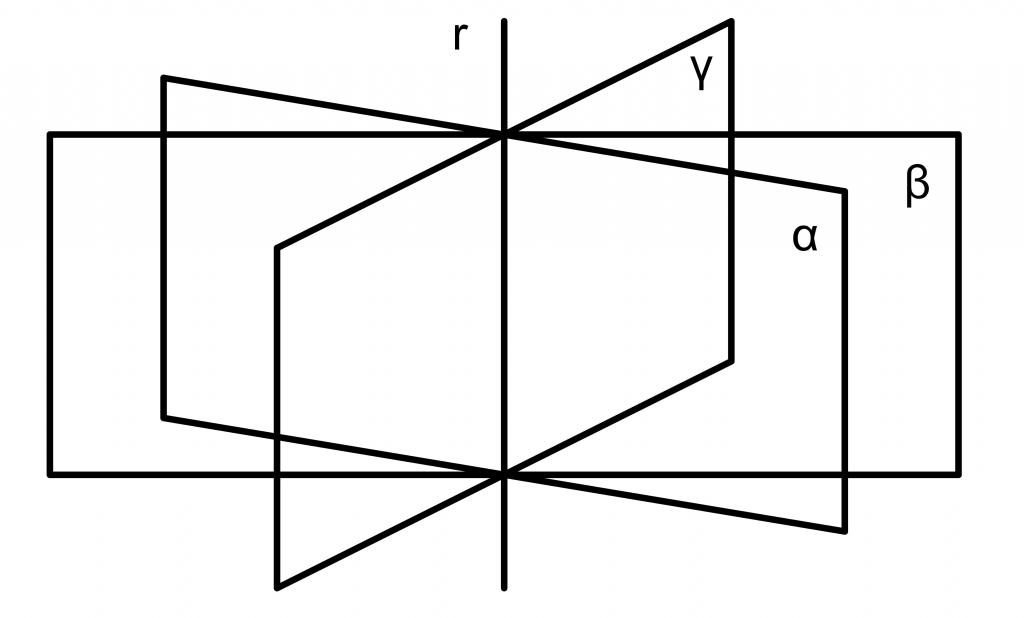
Ако се две равни секу, све њихове заједничке тачке леже на једној правој линији. Треба приметити да је једна од метода за одређивање правца у простору систем од две опште једнаџбе равнине. Колико авиона у свемиру може бити повучено кроз једну равну линију? Бесконачан број. Њихова колекција се зове сноп. Једначина која описује овај пакет има следећи облик:

к ₁ * (А ₁ * к + Б ₁ * и + Ц ₁ * з + Д ₁ ) + к ₂ * (А ₂ * к + Б ₂ * и + Ц ₂ * з + Д ₂ ) = 0.

Овде су к ₁ и к ₂ произвољни бројеви. Посебан случај је ситуација када један или оба параметра к не могу узети вредност нула. Претпоставимо да је к _1, 0, онда се једначина снопа може преписати у облику:

(А ₁ * к + Б ₁ * и + Ц ₁ * з + Д ₁ ) + к ₂ / к ₁ * (А ₂ * к + Б ₂ * и + Ц ₂ * з + Д ₂ ) = 0.

Ова једнакост описује све равнине снопа осим оне која има директни вектор н ₂ ¯ (А ₂ ; Б ₂ ; Ц ₂ ).

Пример снопа авиона је збирка листова отворене књиге.

Затим решавамо неколико геометријских проблема применом добијених знања о својствима равни у простору.

Претворите параметарску векторску једнаџбу у опште

Даје следећу равнинску равнину у параметарском векторском облику:

(к; и; з) = (1; 2; 0) + α * (1; 2; 3) + β * (- 1; 3; 0).

Потребно га је написати као општу једнаџбу равнине у простору.

Преправимо га експлицитно:

к = 1 + α - β;

и = 2 + 2 * α + 3 * β;

з = 3 * α.

Из последњег израза добијамо а, онда га замењујемо у прву једнакост и изражавамо β. Пронађени параметри су замењени у другу једначину, имамо:

α = з / 3;

β = 1 - к + з / 3;

и = 2 + 2 * з / 3 + 3 - 3 * к + з =>

и + 3 * к + 5/3 * з - 5 = 0 =>

9 * к + 3 * и + 5 * з -15 = 0.

Дакле, да би се добила општа једнаџба из параметарског вектора, морамо је прво написати експлицитно, а затим изразити параметре у смислу варијабилних координата.

Претварање општег у параметарску векторску једначину

Овај задатак је потпуно супротан претходном. Размотрите технике за његово решавање.

С обзиром на следећу једначину:

к-2 * и + 3 * з -1 = 0.

За почетак, једна координата треба да се изрази у две. Екпресс на пример к:

к = 2 * и-3 * з +1.

То значи да свака тачка која има координате припадаће равни:

(2 * и-3 * з +1; и; з).

Сада ћемо преписати ову координату као суму три вектора, прва ће садржати само варијаблу и, другу само з, а трећа ће бити само бројеви. Имамо:

(к; и; з) = (2 * и; и; 0) + (-3 * з; 0; з) + (1; 0; 0).

Видљиво је да отварањем ове једначине добијамо опште координате за тачку у равни. Сада остаје само да факторишемо варијабле у првом и другом вектору и редефинишемо их параметрима α и β. Добијамо:

(к; и; з) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0; 1).

Добили смо једначину у параметарском векторском облику, сличну оригиналној.

Слика равнине у координатном систему

Задатак је сљедећи: према познатој једнаџби треба нацртати равнину у простору. Одговарајућа једначина је:

3 * к - и -4 * з +5 = 0.

Да би се приказала ова раван, потребно је пронаћи тачке у којима се сијече координатне оси. Да бисте то урадили, можете добити одговарајућу једначину у сегментима. Међутим, у овом случају настављамо другачије: ставимо двије координате једнаке нули и израчунамо трећу. Имамо:

и = 0; з = 0; к = -5/3;

к = 0; з = 0; и = 5;

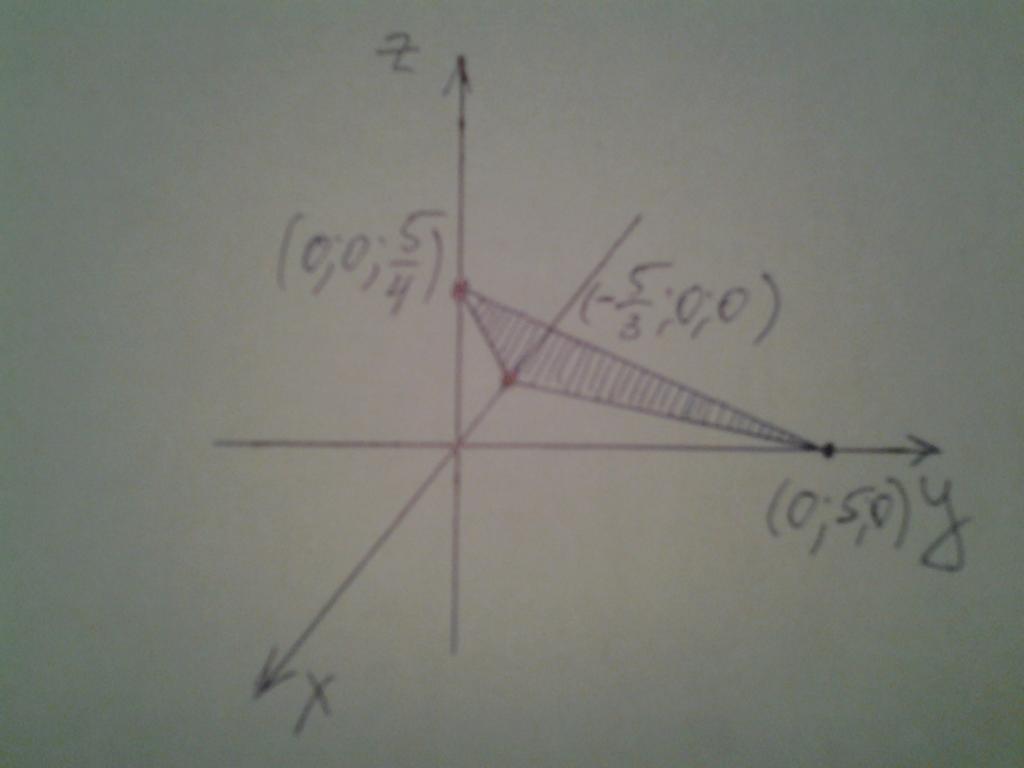
к = 0; и = 0; з = 5/4.

Остаје да се добије добијене тачке на координатне осе и да се кроз њих нацрта раван. Положај равнине у простору приказан је на слици испод.

Три бода и авион

Нека се дају три тачке у простору:

М (1; -1; 3);

Н (3; 2; -4);

Л (2; 5; 0).

Неопходно је пронаћи авион који пролази кроз њих.

Из геометрије је познато да три тачке које не леже на једној линији јединствено одређују раван. Његова једначина може бити састављена ако пронађемо њен вектор који води н¯. Она ће бити једнака векторском производу копланарних вектора који леже у равни. Координате вектора могу се добити из координата тачака, на пример:

МН¯ (2; 3; -7);

МЛ¯ (1; 6; -3).

Њихов векторски производ ће дати вектор н¯. Рачунамо, добијамо:

н¯ (33; -1; 9).

Узимајући на пример тачку М, добијамо општу једначину у облику:

33 * к -и + 9 * з - 61 = 0.

Координате тачака Н и Л можете заменити у једначину и проверити да ли је једнака.