Како је формулисана и доказана косинусна теорема?
Нису сви ученици, а још више одрасли, знали да је косинусна теорема директно повезана са Питагорејском теоремом. Тачније, ово друго је посебан случај првог. Овај тренутак, као и два начина за доказивање косинусне теореме, помоћи ће вам да постанете особа са више знања. Поред тога, пракса изражавања вриједности из оригиналних израза је добро развијено логичко размишљање. Дуга формула теореме која се проучава сигурно ће приморати једног на рад и побољшање.
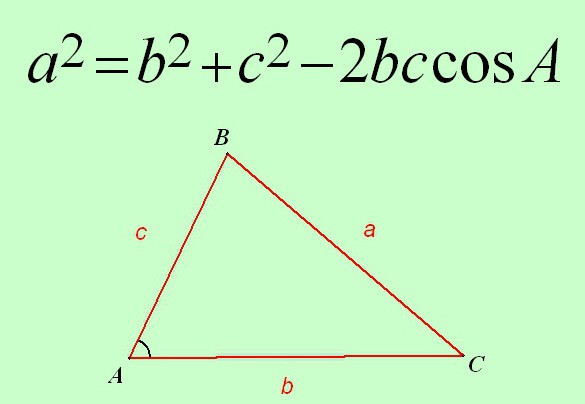
Почетак разговора: увођење симбола
Ова теорема је формулисана и доказана за произвољни троугао. Према томе, она се увек може користити, у свакој ситуацији, ако су дате две стране, ау неким случајевима три, и један угао, а не нужно између њих. Свеједно врста троугла теорема увек ради.
А сада о означавању количина у свим изразима. Боље је да се одмах сложите, како не бисте више пута објашњавали. За ово је састављена следећа табела.
| Триангле елемент | Његова ознака |
| Непозната страна | а |
| Друге две стране | у, са |
| Кут насупрот непознате стране | А |
| Кутеви који леже на другим странама | Б, Ц |
| Висина врха троугла | н |
Формулација и математичко писање
Дакле, косинусна теорема је формулисана на следећи начин:
Квадрат стране било ког троугла је једнак збиру квадрата друге две стране, минус два пута производ истих страна косинусом угла који лежи између њих.
Наравно, то је дуго, али ако разумете његову суштину, онда ће бити лако запамтити. Можете чак и замислити цртеж троугла. Визуално је увек лакше запамтити.
Формула ове теореме ће изгледати овако:
а 2 = 2 + с 2 - 2 * ц * с * цос А.
Мало дуго, али све је логично. Ако погледате мало ближе, видите да се слова понављају, тако да је лако запамтити.
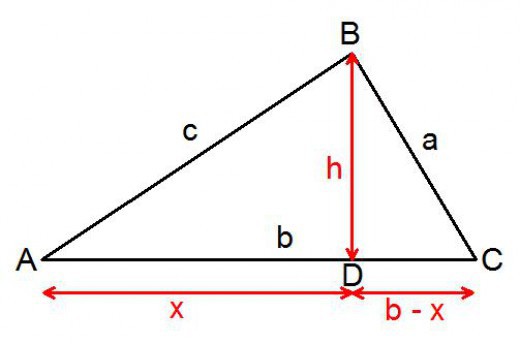
Заједнички доказ теореме
Пошто је валидан за све троуглове, могуће је изабрати за резоновање било који од типова. Нека буде лик са свим оштрим угловима. Размотримо произвољни акутни троугао чији је угао Ц већи од угла Б. Из врха са овим великим углом, требате спустити окомиту на супротну страну. Висина која држи дели троугао на два правоугаоника. Ово је потребно за доказ.
Страна ће бити подељена у два сегмента: к, и. Они се морају изразити у познатим терминима. Део који се испостави да је у троуглу са хипотенузом једнаком, биће изражен писањем:
к = у * цос А.
Други ће бити једнак овој разлици:
и = с - у * цос А.
Сада треба да напишемо Питагорејску теорему за ова два ригхт трианглес узимајући непознату висину. Ове формуле ће изгледати овако:
н 2 = у 2 - (у * цос А) 2 ,
н 2 = а 2 - (ц - ц * цос А) 2 .
У тим једнакостима су идентични изрази на левој страни. Стога ће и њихове десне стране бити једнаке. Лако је писати. Сада морате да отворите заграде:
у 2 - у 2 * (цос А) 2 = а 2 - с 2 + 2 с * у * цос А - у 2 * (цос А) 2 .
Ако изведемо трансфер и редукцију таквих термина, добијамо почетну формулу, која се пише иза текста, тј. Косинусне теореме. Доказ је комплетан.
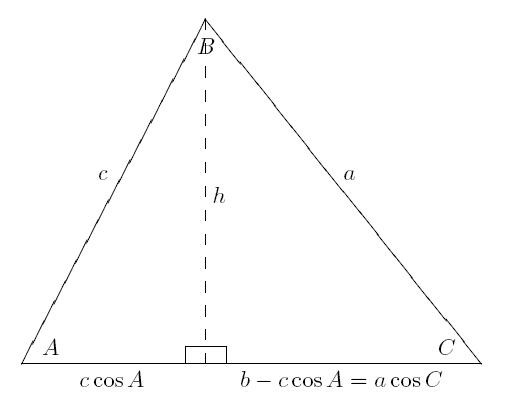
Доказ теореме кроз векторе
Он је много краћи од претходног. А ако знате својства вектора, онда ће се теорија о косинусу за троугао показати једноставно.
Ако су стране а, б, ц означене редом векторима БЦ, АЦ и АБ, онда је једнакост истинита:
СУ = АЦ - АБ.
Сада морате да извршите неке радње. Прва од њих је квадрирање обе стране једнакости:
БЦ 2 = АЦ 2 + АБ 2 - 2 АЦ * АБ.
Тада се једнакост мора преписати у скаларној форми, с обзиром да је производ вектора једнак косинусу угла између њих и њихових скаларних вриједности:
БЦ 2 = АЦ 2 + АБ 2 - 2 АЦ * АБ * цос А.
Остаје само да се вратимо на стару нотацију, и опет ће се појавити косинусна теорема:
а 2 = 2 + с 2 - 2 * ц * с * цос А.
Формуле за друге стране и све углове
Да бисте пронашли страну, из косинусне теореме морате извући скуаре роот. Формула за квадрате једне од других страна ће изгледати овако:
са 2 = а 2 + до 2 - 2 * а * до * цос Ц.
Да би се написао израз за квадрат стране у , потребно је заменити претходну једнакост са од на, и обрнуто, и ставити угао Б.
Из основне формуле теореме можемо изразити вредност косинуса угла А:
цос А = (в 2 + с 2 - а 2 ) / (2 в * с).
Формуле за друге углове су изведене на исти начин. Ово је добра пракса, тако да можете сами покушати да их напишете.
Наравно, нема потребе за памћењем ових формула. Довољно је разумјети теорему и способност извођења тих израза из њеног главног записа.
Првобитна формула теореме омогућава да се пронађе страна ако угао није између два позната. На пример, треба да нађете у , када добијете вредности: а, ц, а . Или је непознато са , али постоје вредности а, б, а .
У овој ситуацији, морате премјестити све формуле додатка лијево. Ова једнакост се добија:
с 2 - 2 * в * с * цос А + в 2 - а 2 = 0.
Поново га напишите у мало другачијем облику:
са 2 - (2 * у * цос А) * са + (у 2 - и 2 ) = 0.
Лако можете видети квадратну једначину. У њему је непозната количина ц , а све остале су дате. Стога је довољно ријешити га уз помоћ дискриминанта. Тако да ће се наћи непозната страна.
Слично томе, добијена је формула за другу страну:
2 - (2 * с * цос А) * ц + (ц 2 - а 2 ) = 0.
Из других израза, такве формуле се лако добијају и сами.
Како израчунати кут без рачунања косинуса?
Ако пажљиво погледате формулу косинусног кута која је добијена раније, приметићете следеће:
- именилац фракције је увек позитиван број, јер садржи производ страна које не могу бити негативне;
- угао ће зависити од знака нумератора.
Угао А ће бити:
- акутна у ситуацији када је нумератор већи од нуле;
- туп ако је тај израз негативан;
- директно када је нула.
Успут речено, ова друга ситуација претвара косинусну теорему у Питагорину теорему. Зато што је за кут од 90º, косинус нула, а последњи термин нестаје.
Први задатак
Цондитион
Тузни угао неког произвољног троугла је 120º. О странама на које је ограничен, познато је да је једна од њих 8 цм дужа од друге, позната је дужина треће стране, она је 28 цм, а потребно је пронаћи периметар троугла.
Решење
Прво морате одредити једну од страна са словом “к”. У овом случају, други ће бити једнак (к + 8). Пошто постоје изрази за све три стране, можете користити формулу коју косинусна теорема даје:
28 2 = (к + 8) 2 + к 2 - 2 * (к + 8) * к * цос 120º.
У табелама за косинус, морате да пронађете вредност која одговара 120 степени. То ће бити број 0,5 са знаком минус. Сада је потребно отворити заграде, поштујући сва правила и дати сличне термине:
784 = к 2 + 16к + 64 + к 2 - 2к * (-0.5) * (к + 8);
784 = 2к 2 + 16к + 64 + к 2 + 8к;
3к 2 + 24к - 720 = 0.
Ова квадратна једначина се решава проналажењем дискриминанта, који ће бити једнак:
Д = 24 2 - 4 * 3 * (- 720) = 9216.
Пошто је његова вредност већа од нуле, једначина има два корена одговора.
к 1 = ((-24) + √ (9216)) / (2 * 3) = 12;
к 2 = ((-24) - √ (9216)) / (2 * 3) = -20.
Посљедњи коријен не може бити одговор на проблем, јер странка мора нужно бити позитивна.
Дакле, две стране су познате. Лако је пронаћи треће: 12 + 8 = 20 (цм). Сада можете одговорити на питање проблема. Периметар троугла дефинише се као збир свих страна:
24 + 12 + 20 = 60 (цм).
Одговор : периметар је 60 центиметара.

Проблем број 2
Цондитион
У троуглу су познати: ц , једнако 2 цм; а , која је 10 цм; угао Ц вредност од 120º. Потребно је пронаћи страну.
Решење
Прво морате користити косинусну теорему и извести формулу квадратна једначина у којој ће вредност у бити непозната:
са 2 = а 2 + у 2 - 2 * а * у * цос Ц
и
в 2 - (2 * а * цос Ц) * в + (а 2 - ц 2 ) = 0.
Потребно је заменити све познате вредности у услову:
в 2 - (2 * 10 * цос 120º) * в + (10 2 - 2 2 ) = 0.
Сада треба да рачунамо шта је могуће да поједноставимо израз:
в 2 - (20 * (-1/2)) * в + (100 - 4) = 0
или
у 2 + 10 * у - 96 = 0.
Ово је стандардна квадратна једначина која се мора решити проналажењем дискриминантног:
Д = (10) 2 - 4 * 1 * (-96) = 484.
Према формулама потребно је извршити калкулације за непознату страну:
у 1 = (- 10 + 22) / 2 = 6 (цм);
у 2 = (- 10 - 22) / 2 = - 16 - овај корен не задовољава решење проблема, јер страна не може бити негативна.
Одговор: непозната страна је 6 цм.
Трећи задатак
Цондитион
У неком троуглу, дате су стране: а, б, ц , које су 6 цм, 10 цм и 8 цм.
Решење
Опет требате користити косинусну теорему. Користи се њен запис, у коме се налази косинус угла А, јер се управо то мора израчунати. Ево формуле за косинус непознатог угла:
цос А = (в 2 + с 2 - а 2 ) / (2 в * с).
Остаје да се замене вредности странака и изврше сви прорачуни:
цос А = (10 2 + 8 2 - 6 2 ) / (2 * 8 * 10).
Након што су сви термини квадрирани и множити бројеве из имениоца:
цос А = (100 + 64 - 36) / (160).
Након додавања и поделе испада:
цос А = 128/160 = 0,8.
Сада требате користити таблицу Брадис да бисте сазнали који је кут А. једнак. Најближа вриједност кута за овај косинус је 36º54´.
Одговор: вредност угла А је 36º54´.