Како израчунати дијагоналу призме равног четверокута?

Призма је геометријска волуметријска фигура, чије се особине и својства проучавају у средњим школама. По правилу, приликом проучавања, узимају се у обзир количине као што су запремина и површина. У овом чланку ћемо отворити нешто другачије питање: дајемо методу за одређивање дужине дијагонала призме примјером четверокутног облика.

Коју фигуру називамо призма?

У геометрији је дата следећа дефиниција призме: она је тродимензионални облик, омеђена двема полигоналним идентичним странама које су паралелне једна другој, и бројем паралелограма. Доња слика показује пример призме која задовољава ову дефиницију.

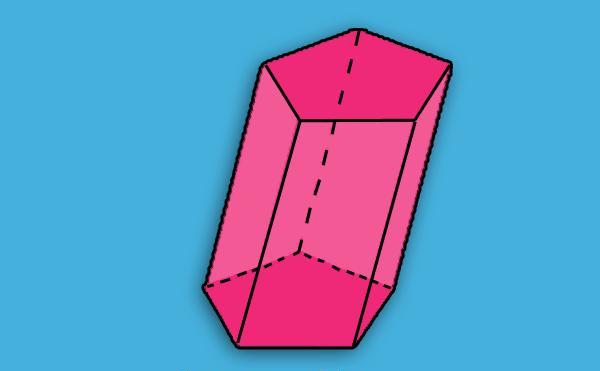
Видимо да су два петерокута једнака један другом и налазе се у две паралелне равни. Пет ружичастих паралелограма повезује ове петерокуте у један објект - призму. Два пентагона се називају основе фигуре, а паралелограми су бочна лица.

Призме су равне и накошене, које се називају и правоугаоним и косим. Разлика између њих је у угловима између базе и бочних страна. За правокутну призму, сви ови углови су 90 ^о .

Према броју страна или врхова полигона у бази, они говоре о призмама троугластих, петерокутних, четверокутних и тако даље. А ако је овај полигон тачан, а сама призма је равна линија, онда се такав облик назива коректним.

Призма приказана на претходној слици је петерокутна. Испод је петерокутна равна призма, која је исправна.

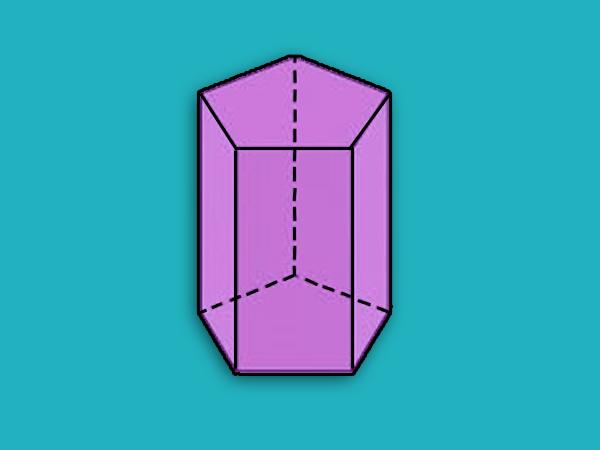
Све калкулације, укључујући и метод одређивања дијагонале призме, погодно је да се изведу тачно за тачне цифре.

Који елементи карактеришу призму?

Елементи слике су саставни делови који га формирају. Конкретно за призму, постоје три главне врсте елемената:

• пеакс;
• лица или стране;
• ребра.

Лица су базе и бочне равнине које представљају паралелограле у општем случају. У призми, свака страна је увек једна од две врсте: или је то полигон или паралелограм.

Рубови призме су они сегменти који ограничавају сваку страну фигуре. Као и ивице, ивице су такође два типа: припадају бази и бочној површини или припадају само бочној површини. Први је увек два пута већи од другог, без обзира на врсту призме.

Вртине су тачке пресека три ивице призме, од којих две леже у равни базе, а трећа припада двема бочним странама. Сви врхови призме налазе се у равни основице фигуре.

Бројеви описаних елемената повезани су у једну једнакост, која има сљедећи облик:

П = Б + Ц - 2.

Овде је П број ивица, Б - врхова, Ц - страна. Ова једнакост се назива Ејлерова теорема за полиедер.

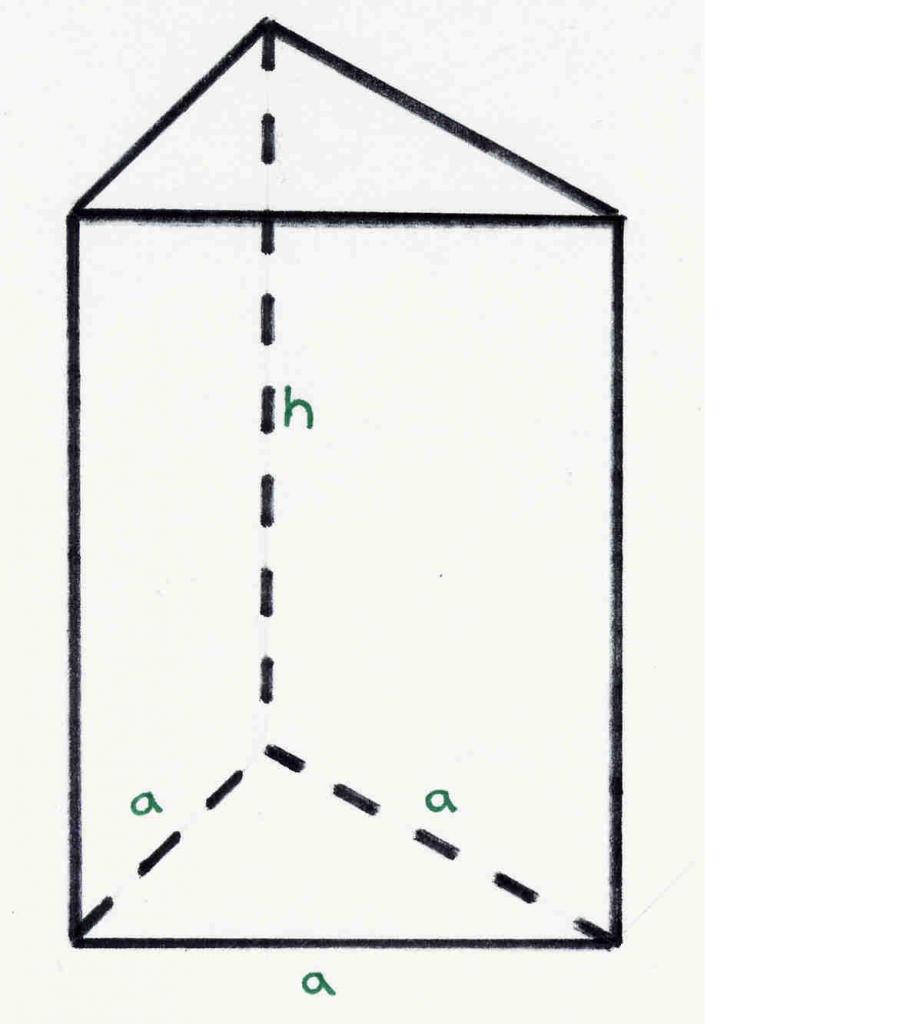
Слика приказује троугласту исправну призму. Свако може наћи да има 6 врхова, 5 страна и 9 рубова. Ови бројеви су конзистентни са Еулеровом теоремом.

Дијагоналне призме

Након својстава као што су запремина и површина, у проблемима у геометрији, често се проналазе информације о дужини дате дијагонале разматране фигуре, које се или даје или треба пронаћи користећи друге познате параметре. Размотрите шта је дијагонала призме.

Све дијагонале можемо поделити у два типа:

1. Лежи у равни лица. Они повезују не-сусједне врхове полигона на дну призме или паралелограма бочне површине. Вредност дужина таквих дијагонала одређује се на основу познавања дужина одговарајућих ивица и углова између њих. Да би се одредиле дијагонале паралелограма, увек се користе својства троуглова.
2. Лежи унутар волумена призме. Ове дијагонале повезују не-један-на-један врхове две базе. Ове дијагонале су у потпуности унутар слике. Њихова дужина је нешто теже израчунати него за претходни тип. Метода израчунавања подразумева узимање у обзир дужина ивица и базе и паралелограма. За равне и регуларне призме, прорачун је релативно једноставан, јер се изводи уз помоћ Питагорине теореме и својстава тригонометријских функција.

У наставку су дати примери израчунавања различитих дијагонала.

Дијагоналне стране четверокутне равне призме

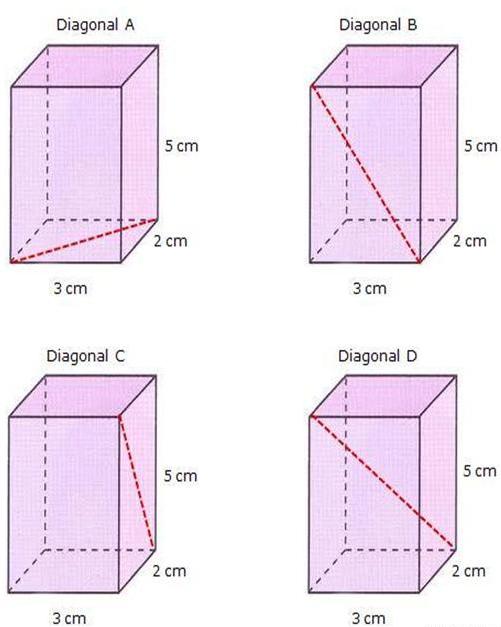
На слици изнад приказане су четири идентичне равне призме, а дати су и параметри њихових ивица. На призмама Дијагонала А, Дијагонале Б и Дијагонале Ц црвена црвена линија приказује дијагоналу три различита лица. Пошто је призма равна са висином од 5 цм, а база је представљена правоугаоником са странама од 3 цм и 2 цм, лако је пронаћи означене дијагонале. Да бисте то урадили, користите Питагорову теорему.

Дужина дијагонале основе призме (Дијагонала А) је једнака:

Д _А = √ (3 ² +2 ² ) = 13 ≈ 3.606 цм.

За бочну страну призме, дијагонала је (види Дијагонала Б):

Д _Б = √ (3 ² + 5 ² ) = 34 ≈ 5.831 цм.

На крају, дужина друге стране дијагонале је једнака (види Дијагонала Ц):

Д _Ц = √ (2 ² + 5 ² ) = 29 ≈ 5.385 цм.

Дужина унутрашње дијагонале

Сада израчунавамо дужину дијагонале четверокутне призме, која је приказана на претходној слици (Дијагонала Д). То није тако тешко урадити ако приметите да је то хипотенуза троугла, у којој ће висина призме (5 цм) и дијагонала Д _А приказана на слици у горњем левом углу (Дијагонала А) бити ноге. Онда добијамо:

Д _Д = √ (Д _А ² + 5 ² ) = √ (2 ² +3 ² +5 ² ) = 38 ≈ 6.164 цм.

Правилна призма четвороугла

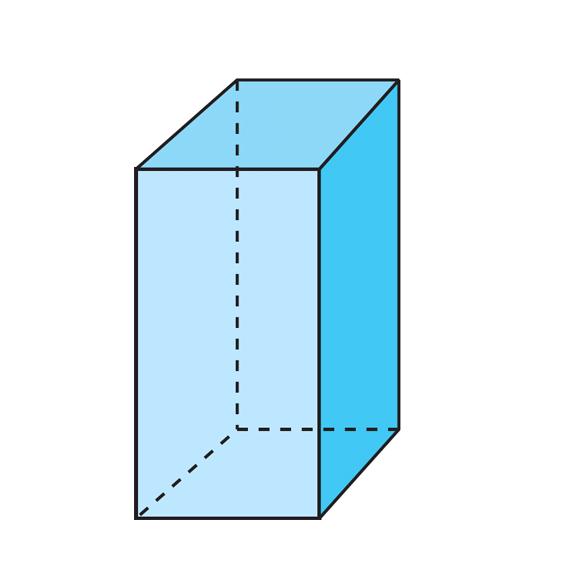
Дијагонала регуларне призме, чија је основа квадрат, израчунава се на исти начин као у горњем примеру. Одговарајућа формула је:

Д = √ (2 * а ² + ц ² ).

Где су а и ц дужине основне и бочне ивице, респективно.

Имајте на уму да смо у прорачунима користили само Питагорину теорему. Да би се одредиле дужине дијагонала регуларних призми са великим бројем врхова (петерокутна, шестерокутна и тако даље), већ је потребно користити тригонометријске функције.