Како пронаћи квадрат дијаманта? Могући начини проналажења одговора
Математика је школски предмет који сви уче, без обзира на профил класе. Међутим, она није вољена од свих. Понекад неправедно. Ова наука непрестано баца студенте на задатке који омогућавају њихов развој. Математика се сналази како не би дала менталне способности деци да избледе. Једна од његових секција се бави овим, посебно добро - геометријом.
Било која од тема које се проучавају у њој заслужује пажњу и поштовање. Геометрија је начин да се развије просторна имагинација. Пример је тема квадрата фигура, посебно дијаманата. Ове слагалице могу довести до ћорсокака, ако не разумете детаље. Зато што су могући различити приступи проналажењу одговора. Неко ће лакше запамтити различите верзије формула, које су написане испод, а неко их може добити из претходно наученог материјала. У сваком случају, безнадежне ситуације се не дешавају. Ако мало помислите, решење ће сигурно бити пронађено.
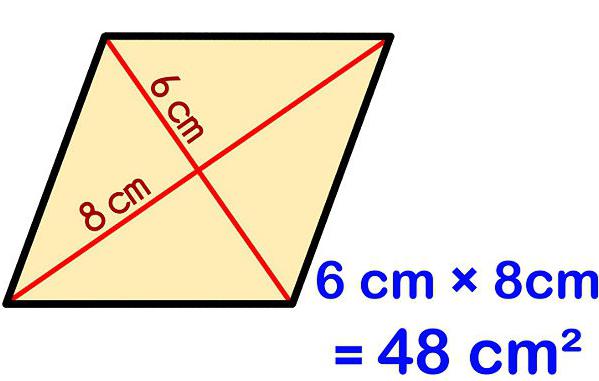
Шта је ромб и како изгледа као други квадрилатерали?
Одговорите на ово питање да бисте разумели принципе добијања формула и ток расуђивања у проблемима. Уосталом, да бисте схватили како да пронађете подручје ромба, морате јасно разумети каква је то фигура и које су њене особине.
Ради лакшег разматрања паралелограма, који је четвороугао са паралелним странама, узет ћемо "родитеља". Он има два "детета": правоугаоник и ромб. Оба су паралелограми. Ако наставимо паралеле, ово је "презиме". Дакле, да би пронашли рхомбус ареа Можете користити већ проучену формулу паралелограма.
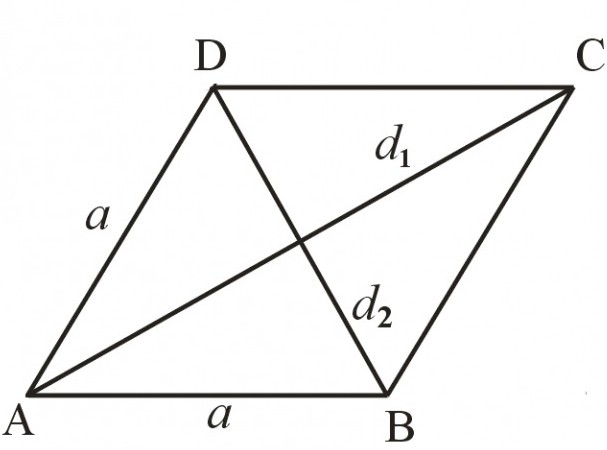
Али, као и сва деца, ромб има нешто своје. Ово се мало разликује од "родитеља" и може се сматрати засебном фигуром. На крају крајева, правоугаоник није ромб. Враћајући се на паралеле - они су као брат и сестра. Имају много тога заједничког, али се и даље разликују. Ове разлике су њихове посебне особине које треба користити. Било би чудно знати о њима и не примењивати у решавању проблема.
Ако наставимо аналогију и запамтимо другу фигуру - квадрат, онда ће то бити наставак ромба и правоугаоника. Ова бројка комбинује сва својства једног и другог.
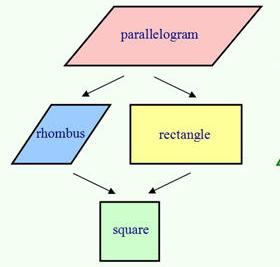
Диамонд пропертиес
Има их пет и наведени су у наставку. Неки од њих понављају својства паралелограма, а неки су својствени само оној слици.
- Ромб је паралелограм који је добио посебан облик. Из овога следи да су његове стране паралелно паралелне и једнаке. Штавише, они су неуједначени у паровима, и то је све. Као што би имао квадрат.
- Дијагонале овог четворокутног пресека се под углом једнаким 90º. Ово је згодно и увелико поједностављује ток расуђивања при рјешавању проблема.
- Још једна особина дијагонала: свака од њих је подељена тачком укрштања на једнаке сегменте.
- Углови који леже један наспрам другог су једнаки.
- И последње својство: дијагонала ромба се поклапа са симетралима углова.
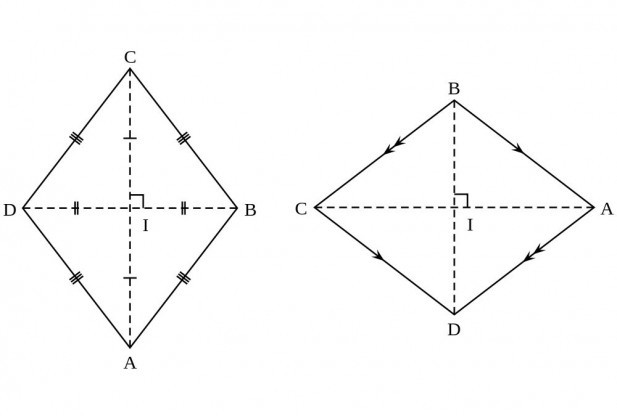
Ознаке које се прихватају у разматраним формулама
У математици је потребно ријешити проблеме користећи заједничке изразе слова, који се називају формуле. Тема трга није изузетак.
Да бисте отишли до записа који вам говоре како пронаћи подручје ромба, морате се сложити око слова која замјењују све нумеричке вриједности елемената фигуре.
Назив ставке | Ознака |
диамонд сиде | а |
велика дијагонала | Д 1 |
смалл диагонал | Д 2 |
диамонд хеигхт | Х |
акутни угао | А |
туп кут | Ин |
радијус исписан у круг | заједничка нотација у математици |
фигуре ареа |
Сада је време да напишете формуле.
Међу подацима о задацима постоје само дијагонални дијаманти.
Правило каже да се за проналажење непознате количине мора помножити дужина дијагонала, а затим подијелити производ на пола. Резултат поделе је површина ромба преко дијагонала.
Формула за овај случај ће изгледати овако:
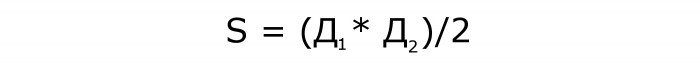
Нека ова формула иде на број 1.
Задатак се даје страни дијаманта и његовој висини
Да бисте израчунали површину, потребно је да пронађете производ ове две количине. Можда је то најједноставнија формула. Штавише, из теме је познато подручје паралелограма. Тамо је таква формула већ проучена.
Писање математике:
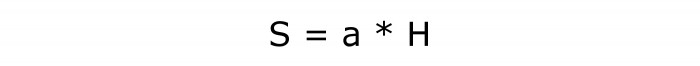
Број ове формуле је 2.
Познати страни и оштар угао
У овом случају, потребно је квадрирати величину стране ромба. Онда пронађите синус угла. И трећи корак је израчунати производ формираних две количине. Одговор ће бити дијамантски квадрат.
Литерални израз:
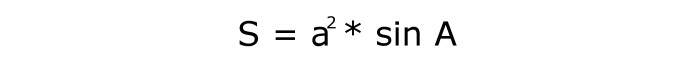
Његов серијски број је 3.
Ове вредности: полупречник уписане кружнице и оштар угао
Да бисте израчунали површину ромба, морате пронаћи квадрат радијуса и помножити га са 4. Одредите вредност синуса угла. Затим поделите производ са другом количином.
Формула има следећи облик:
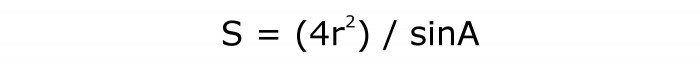
То ће бити нумерисано 4.
Проблем обухвата страну и радијус уписане кружнице.
Да бисте утврдили како пронаћи подручје ромба, потребно је израчунати производ тих количина и број 2.
Формула за овај задатак ће изгледати овако:
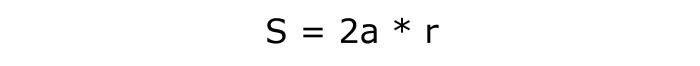
Њен број је у реду - 5.
Примери могућих задатака
Задатак 1
Једна од дијагонала ромба је 8, а друга 14 цм, а потребно је пронаћи подручје фигуре и дужину његове стране.

Решење
Да бисте пронашли прву вредност, потребна вам је формула 1, у којој Д 1 = 8, Д 2 = 14. Тада се површина израчунава на следећи начин: (8 * 14) / 2 = 56 (цм2).
Дијагонале раздвајају дијамант на 4 троугла. Сваки од њих ће бити правоугаоног облика. Ово се мора користити за одређивање вредности друге непознате. Страна ромба ће постати хипотенуза троугла, а ноге ће бити половина дијагонала.
Тада а 2 = (Д 1/2 ) 2 + (Д 2/2) 2 После замене свих вредности добијамо: а 2 = (8/2) 2 + (14/2) 2 = 16 + 49 = 65. Али ово је квадрат са стране. Тако да треба да извадите скуаре роот од 65. Онда ће дужина стране бити приближно једнака 8.06 цм.
Одговор: површина је 56 цм 2 , а страна 8,06 цм.
Задатак 2
Дијамантна страна има вредност од 5,5 дм, а висина му је 3,5 дм. Нађите подручје на слици.
Решење
Да би се пронашао одговор, биће потребна формула 2. У њој, а = 5.5, Х = 3.5. Затим, замењујући слова у формули бројевима, добијамо да је жељена вредност 5.5 * 3.5 = 19.25 (дм 2 ).
Одговор: површина ромба је једнака 19,25 дм 2 .
Задатак 3
Оштар угао ромба је 60º, а његова мања дијагонала је 12 цм.
Решење
Да бисте добили резултат, биће вам потребна формула број 3. У њој ће умјесто А бити 60, а вриједност а је непозната.
Да бисте пронашли страну ромба, морате се сјетити синусне теореме. У правом троуглу, а ће бити хипотенуза, мања нога је једнака половини дијагонале, а угао је подељен на пола (познат из својства где се помиње симетрала).
Тада ће страна а бити једнака производу ноге на синусу угла.
Нога се мора израчунати као Д / 2 = 12/2 = 6 (цм). Синус (А / 2) ће бити једнак његовој вредности за угао од 30º, односно 1/2.
Извођењем једноставних калкулација добијамо следећу вредност стране ромба: а = 3 (цм).
Сада је површина производ 3 2 и синус 60º, односно 9 * (√3) / 2 = (9√3) / 2 (цм2).
Одговор: жељена вредност је (9√3) / 2 цм2.
Резултати: све је могуће
Овде су разматране неке опције за проналажење подручја дијаманта. Ако није јасно у проблему директно коју формулу користити, онда морате мало размислити и покушати да повежете претходно проучене теме. У другим темама увек постоји наговештај који ће помоћи да се познате вредности повежу са онима у формулама. И проблем ће бити решен. Главно је запамтити да све што је претходно проучено може и треба да се користи.
Поред предложених задатака, могући су и инверзни проблеми, када је на површини фигуре потребно израчунати вредност дијамантног елемента. Затим морате користити једнаџбу која је најближа услову. И онда претворите формулу, остављајући непознату вредност на левој страни једнакости.